1. Що називається конфліктною ситуацією?

Конфліктною називається ситуація, коли стикаються інтереси двох чи більше сторін, які мають суперечливі цілі, причому виграш кожної зі сторін залежить від того, як поводитимуться інші.

2. Що таке гра?

Гра - це ідеалізована математична модель колективного поводження декількох осіб (гравців), інтереси яких різноманітні, що і породжує конфлікт

3. Що таке хід гри?

У процесі гри її учасники здійснюють ходи. Ходом гравця називається вибір та здійснення однієї із передбачених правилами дій. Ходи бувають особистими і випадковими. Хід називається особистим, якщо гравець свідомо вибирає його із сукупності можливих варіантів дії і здійснює його (наприклад, будь-який хід у шаховій грі). Хід називається випадковим, якщо його вибір провадиться не гравцем, а яким-небудь механізмом випадкового вибору (наприклад, по результату кидання монети).Сукупність ходів початих гравцями від початку до закінчення гри, називається партією.

4. Дайте визначення платіжної матриці.

Платіжна матриця – це таблиця, в якій показані виплати кожному учаснику при двосторонній грі. Рядки таблиці відображають результати кожного вибору стратегії одним учасником, а стовпці - результати вибору іншого. Може існувати одна матриця, що показує виграш кожного гравця, а також альтернативний варіант, коли кожен квадрат в багатовимірної платіжної матриці може містити два числа, щоб показати виплати обом гравцям.

5. С формулюйте принцип мінімаксу?

Принцип мінімаксу. В теорії ігор принцип обережності, який рекомендує гравцям дотримання максимінної і мінімаксної стратегій, називається принцип мінімаксу. Він випливає з припущення про обережність гравців, тобто з бажання розв'язати конфліктну ситуацію найкращим чином для всіх учасників конфлікту.

Принцип мінімаксу : вибирай ту стратегію. щоб при найгіршому для нас поводженні супротивника одержати максимальний виграш.

6. Дайте визначення максимінної та мінімаксної стратегії.

Максимін - це максимальний виграш, який гравець А може собі гарантувати в грі проти розумного противника. Якщо гравець А буде дотримуватись максимінної стратегії, то йому при будь-якої розумної поведінці гравця В гарантовано виграш, не менший ніж . Стратегія, яка відповідає максиміну називається максимінною.

Мінімакс - це мінімальний програш, який гравець В може собі дозволити в грі проти розумного противника. Якщо гравець В буде дотримуватись найбільш обережної з усіх стратегій - мінімаксної - то йому при будь-якої випадку забезпечено програш, не більший ніж . Стратегія, яка відповідає мінімаксу називається мінімаксною.

7. Яка гра називається скінченною, парною?

Якщо в грі беруть участь два гравці, то така гра називається парною (грою двох осіб). Якщо кожен гравець має скінченну кількість стратегій, то гра — скінченна.

8. Які властивості мають оптимальні стратегії гравців?

Задачею кожного гравця є знаходження оптимальної стратегії, яка за умови багатократного повторення гри забезпечує даному гравцю максимально можливий середній виграш.

9. Сформулюйте основну теорему теорії ігор.

Теорема Неймана (основна теорема теорії ігор). Кожна скінченна гра має, принаймні, один розв'язок, можливий в області змішаних стратегій.

10. У який спосіб здійснюється зведення гри до задачі лінійного програмування?

Для розв'язування гри використовують прийом зведення її до задачі лінійного програмування. Нехай розглядається парна гра зі стратегіями для гравця А та стратегіями для гравця В і платіжною матрицею . Необхідно знайти оптимальні змішані стратегії і , де , .

Знайдемо спочатку оптимальну стратегію гравця А. За основною теоремою теорії ігор така стратегія має забезпечити гравцеві виграш, не менший за ціну гри (поки що невідому величину) , за будь-якої поведінки гравця В.

Допустимо, що гравець А застосовує свою оптимальну стратегію, а гравець В - свою «чисту» -ту стратегію , тоді середній виграш гравця А дорівнюватиме:

. (1)

За цих обставин виграш має бути не меншим, ніж ціна гри. Отже, для будь-якого значення величина виду (1) має бути не меншою, ніж :

Розділивши всі обмеження на , отримаємо:

Позначивши , маємо :

, .

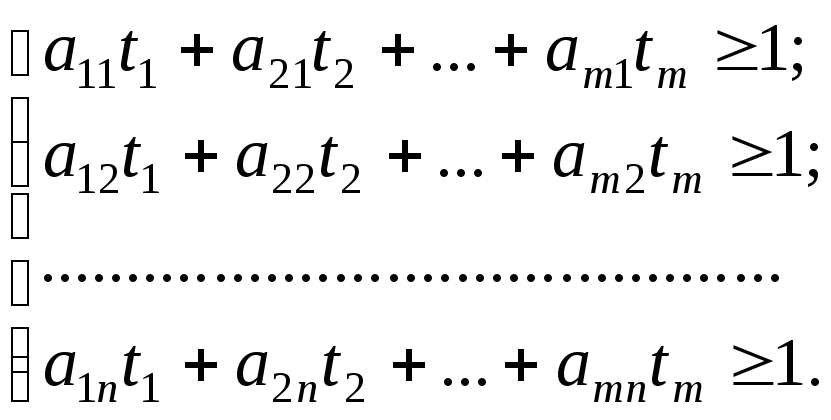Враховуючи умову, що отримуємо .

Необхідно зробити виграш максимальним. Цього можна досягти, коли вираз набуватиме мінімального значення. Отже, врешті маємо звичайну задачу лінійного програмування.

Цільова функція: за умов

, .

Розв'язуючи цю задачу симплексним методом, знаходимо значення , а також величину і значення , що є оптимальним розв'язком початкової задачі. Отже, визначено змішану оптимальну стратегію для гравця А.

За аналогією можна записати задачу лінійного програмування для визначення оптимальної стратегії гравця В. З цією метою позначимо: . Маємо таку лінійну модель задачі: за умов

, .

Очевидно, що задача лінійного програмування для гравця В є двоїстою до задачі гравця А, а тому оптимальний розв'язок однієї з них визначає також оптимальний розв'язок спряженої.

11. Чим визначається гра в нормальній формі?

Визначимо поняття «гри в нормальній формі». В кожній грі приймає участь певна кількість учасників. Кожен гравець, очевидно, має свій інтерес до результатів гри. Зрозуміло, що для досягнення своїх інтересів гравці виконують певні дії. Тоді, тріаду елементів {X_і, U_i , N} де X_і - множина стратегій i-го гравця (альтернативи); U_i - функція виграшу і-го гравця (критерії і-го гравця); N = {1,2...n} -множина гравців, а n - їх кількість називають «грою в нормальній формі і позначають С = { X_і, U_i , N }.

Ігри в нормальній формі – це статичні ігри, коли всі гравці приймають рішення одночасно. При цьому вони не знають, яку саме стратегію обирають інші гравці. У нормальній, або стратегічній, формі гра описується платіжною матрицею. Кожна сторона (точніше, вимірювання) матриці - це гравець; рядки визначають стратегії першого гравця, а стовпці - другого. На перетині двох стратегій можна побачити виграші, які отримають гравці.

12. Означення рівноваги Неша.

Рівновагою Неша називається сукупність стратегій або дій, згідно з якими кожен учасник реалізує оптимальну стратегію, передбачаючи дії суперників. Це така сукупність статегій та виграшів, при якій жоден із учасників не може збільшити виграш, змінивши вибір стратегії в односторонньому порядку, коли інші учасники не змінюють свого вибору.

Рівновага Неша - результат, в якому стратегія кожного з гравців є найкращою серед інших стратегій, що прийняті рештою учасників гри. Воно виходить з того, що жоден з гравців зміною власної ролі не може досягти найбільшої користі («максимізації функції вигідності»), якщо решта учасників твердо дотримуються власної лінії поведінки.

13. Основні теореми для антагоністичних ігор.

Теорема (про активні стратегії). Якщо один з учасників гри притримується своєї оптимальної змішаної стратегії, то очікуваний виграш залишиться незмінним і рівним ціні гри незалежно від дій іншого учасника в межах його активних стратегій.

Теорема Неша. Кожна скінченна антагоністична гра має рішення в змішаних стратегіях.

Афінне правило. Оптимальні стратегії гравців у матричних іграх, елементи матриць А та С яких пов’язані рівностями :

, де λ>0, μ-довільне, мають однакові рівновісні ситуації (або в чистих, або в змішаних стратегіях), а їх ціни задовольняють слідкуючій умові: .

14. Змішані стратегії в грі.

Якщо матрична гра не має сідлової точки, то виникає необхідність гри в змішаних стратегіях. Змішані стратегії представлять математичну модель мінливої і гнучкої тактики гравця, при якій його противник не може довідатись заздалегідь про те становище, в якому йому доведеться опинитись. Перед кожною партією відбувається випадковий вибір однієї з чистих стратегій з деякою певною і вже визначеною ймовірністю. Гравці вибирають стратегії випадково і незалежно один від одного, тому гра має випадковий характер і сума виграшу теж стає випадковою.

Ймовірності (або частоти) вибору кожної стратегії задаються відповідними векторами:

для гравця А – вектор , де ; для гравця В – вектор , де .

Очевидно, що ; .

15. Ітераційний метод Брауна-Робінсона.

Ідея його в наступному - розігрується "уявний експеримент", у якім сторони А и В по черзі застосовують друг проти друга свої стратегії, прагнучи виграти побільше (програти поменше). Кожен з гравців слідкує за діями супротивника і старається відповісти на них найбільш вигідним для себе чином. Експеримент складається з ряду "партій" гри. Починається він з того, що один із гравців (скажімо, А) вибирає довільно одну зі своїх стратегій A_i.

Першу стратегію гравцю доцільно вибрати за принципом Arg i {} ( i- рядок, що забезпечує нижню ціну гри). Супротивник (В) відповідає йому тією зі своїх стратегій B_j яка найвигідніша для нього, тобто обертає його програш при стратегії A_i в мінімум – Arg j {} (обирає j – стовпчик, що забезпечує мінімальний програш при вибраній гравцем А стратегії). Далі знову черга А - він відповідає В тій своєю стратегією А_k, яка дає максимальний виграш при стратегії В_j гравця В – Arg i {} . Далі - знову черга супротивника. Він відповідає своєю стратегією, яка мінімізує програш вже не відносно останньої, застосованої гравцем А стратегії А_k, а відносно накопичуваного виграшу гравця А - a_k1^/ =a_i1 +a_к1 ,a_k2^/ =a_i2 +a_к2 , … ,a_kм^/ =a_iм + +a_км , як сумарного виграшу при застосуванні стратегій A_i, A_k (гравець В обирає стовпчик j=Arg j{} ). І так далі: на кожному кроці ітераційного процесу кожен гравець відповідає на черговий хід іншого своєю стратегією, яка є оптимальною щодо накопичуваного виграшу (програшу). Хід гри зручно відобразити в таблиці (див. табл.2.1)

Таблиця 2.1 Ітераційний метод Брауна - Робінсона

№ гри

Стратегія гравця А

Накопичуваний виграш гравця А

Стратегія гравця В

Накопичуваний програш гравця В

U

W

ν

1

Аi

ai1

ai2

…

aim

Bj

a1j

a2j

…

anj

U1

W1

ν1

2

Аk

ak1/

ak2/

…

akm/

Bl

a1l/

a2l/

…

anl/

U2

W2

ν2

…

…

…

…

…

…

…

…

…

…

…

…

…

…

N

Ap

ap1/

ap2/

…

apm/

Bt

a1t/

a2t/

…

ant/

UN

WN

νN

В таблиці представлені також нижня оцінка ціни гри U, що обчислюється як найменший середній виграш гравця А: , а також верхня оцінка ціни гри W, як найбільший середній програш гравця В :, ν =(U+W)/2 - наближена оцінка ціни гри, як середнє арифметичне між U та W.

Сформулюємо правило зупинки. Нехай задано число ε >0. Процес ітерацій зупинимо на кроці n, коли вперше виконається нерівність . Тоді ціна гри ν .

Змішані стратегії гравців знаходимо за формулами статистичного визначення ймовірностей:

де - загальна кількість використання гравцем А стратегії A_i та відповідно гравцем В стратегії B_j .

16. Біматричні ігри та їх відмінність від матричних.

Скінченні безкоаліційні парні ігри з ненульовою сумою називають біматричними. Біматричні ігри задаються парою матриць виграшів A = ||a_ij|| і B = ||b_ij|| однакових розмірів. Якщо перший гравець вибирає рядок i, а другий — стовпчик j, то виграш першого гравця — a_ij, а другого — b_ij. Або біматричні ігри описуються за допомогою складеної матриці, елементами якої є пари виграшів обох гравців.

Від матричних відрізняються тим, що програш одного гравця не дорівнює виграшу іншого, а також тим, що для біматричних ігор окрім рівноваги Неша існують також рівноваги Парето та Штакельберга.

17. Знаходження рівноваги Неша в біматричних іграх.

Для першого гравця обираємо найкращі відповіді на дії другого гравця. Для другого гравця проводимо аналогічні дії. Якщо у вихідній матриці одержимо ситуацію, коли в будь-якого її подвійного елемента будуть відмічені обидва виграші, то значить у грі відбувається РН, які представляють собою рядок для першого гравця та стовпчик для другого, на перетині яких знаходиться відмічений подвійний елемент.

18. Знаходження рівноваги Парето в біматричних іграх.

Рівновага Парето – це така ситуаціяв грі, з якої неможливо вийти жодному гравцеві з метою збільшити свій виграш, не зменшуючи при цьому виграш інших учасників гри.

Алгоритм пошуку:

Вибираємо певну комірчину в таблиці, яка задає виграші осіб, і, перебираючи всі інші комірчини, порів­нюємо значення виграшів гравців між собою. Якщо в якійсь комірчині можлива ситуація, коли обидва гравців виграють — то ми цю, вибрану нами комірчину, відкидаємо. Дійсно, вона не може бути Парето-оптимумом, бо можливим є одночасне поліпшення виграшів дія обох гравців.

Якщо ж є така комірчина, в якій поліпшення (збільшення!) виграшу одного із гравців можливе лише тільки за умови погіршення (зменшення!) виграшу іншого гравця, - і так для кожної іншої комірчини — то ми знай­шли стратегії, які задають оптимум Парето.

19. Знаходження рівноваги Штакельберга в біматричних іграх.

Рівновагою Штакельберга з лі­дером, який має номер 1, називається така сукупність стратегій всіх інших гравців, що перший гравець (лідер) з урахуванням цілей інших гравців прогнозує рівновагу Неша, яка буде складатися між ними після його ходу, і відповідно до цього оптимізує свою стратегію. Інші ж гравці вибирають стратегію відповідно до його прогнозу.

Алгоритм пошуку:

1. Розглядаємо першу стратегію лідера. Вибираємо той виграш, який є найбільшим для другого гравця. Фіксуємо відповідний виграш лідера (тобто той, який знаходиться в тій же комірчині).

2. Робимо так для кожної стратегії лідера.

3. Розглядаємо множину всіх виграшів лідера, які ми відмітили, і вибираємо найбільший.

4. Стратегія лідера, якій відповідає виділена нами комірчина, і є рі­шенням Штакельберга для нашої задачі.

5. Оскільки маємо всього 2 гравці, то всі концепції виграшів для «ін­шого» гравця зводять до вибору його максимального виграшу у відповідь на хід лідера, і тому рішення Штакельберга для першого гравця є одночасно також і рівновагою Штакельберга для лідера -першого гравця.

Ми можемо розглянути також і другого гравця як лідера — і знайти рівновагу Штакельберга також і для нього інколи ці рівноваги співпада­ють (тобто «все рівно», хто із гравців ходить першим).

20. Домінуючи стратегії та спрощення гри.

Для заданого гравця стратегія у і називається строго (си­льно) домінованою стратегією у₂ , якщо для до­вільної обстановки (тобто для y-_i ) виконана нерівність

i, y-_{i -i} , yⁱ_{1 ,} уⁱ₂ є А_і f_i(уⁱ_{2 ,} y-_i)>f_l(yⁱ_{1 ,} y-_i) (2.2.1),

Коли стратегія у₁ строго домінується стратегією у₂, це означає, що стратегію у₁ взагалі можна відкинути і не розглядати надалі. Дійсно, у від­повідності до (2.2.1), стратегія у₂ є вигіднішою для даного гравця, і тому стратегію у₁ він просто не повинен використовувати.

Звертаємо увагу на те, що тут неявно використано припущення про те, що наш гравець є раціональніш, тобто він орієнтується лише та отри­мання більшого виграшу.

Видалення домінованих стратегій, якщо воно навіть не дозволяє отримати рівновагу в домінантних стратегіях, завжди зменшує обсяг інфо­рмації, яку нам потрібно аналізувати. Це має місце внаслідок того, що ми відкидаємо деякі стратегії для гравців, тобто зменшуємо набір тих страте­гій, якими вони можуть користуватися.

Але далеко не завжди в результаті видалення домінованих стратегій ми можемо отримати єдину стратегію для кожного із гравців.

21. Динамічні ігри.

Динамічною зветься гра, в якій гравці здійснюють ходи послідовно. Різна ступінь інформованості гравців про поточний стан гри дозво­ляє виділити такі класи ігор.

Гра називається грою із досконалою інформацією у тому випадку, коли кожен гравець може однозначно ви­значити своє місце в часовому розгортанню гри (тобто коли відсутні одно­часні ходи і коли всі гравці спостерігають за «ходами Природи»).

Гра із недосконалою інформацією має місце в тому випадку, коли порушуються умови наведеного вище визначення.

Надамо визначення гри в динамічній формі.

1. Задана конечна множина гравців І={1,2,...,п).

2. Задане дерево гри (тобто граф, який визначає послідовність ходів) із конечною множиною вершин АЧ конечною множиною ходів А.

3. Ребра графа (дуги, які з'єднують попередню та наступну вершини) відповідають ходам того чи іншого гравця.

4. Вводиться набір інформаційних множин, який структурований та­ким чином, що всі вершини, які відносяться до одної інформаційної мно­жини, мають одні й ті ж самі допустимі ходи.

5. Співвідношення, яке визначає того гравця (для Природи і=0), який саме й буде ходити, використовуючи відомості даної інформаційної мно­жини.

6. Ймовірності вибору Природою того чи іншого варіанту хода (зви­чайно, сума всіх ймовірностей для одного ходу Природи повинна дорівню­вати 1).

7. Функції виграшів для конечних для даної гри вершин (термінальних вершин).

Таким чином, динамічна гра є грою із досконалою інформацією у ви­падку, коли в кожній вершині гравець не тільки володіє всією повнотою інформації, але й чітко знає свої наступні ходи.

22. ^{Дерево гри.}

^{Дерево гри – це граф, який визначає послідовність ходів.} Дерево гри повинне бути побудоване таким чином, що мати всього одну вершину, із якої починається гра. Необхідно також, щоб із кожної ве­ршини всередині дерева можна було однозначно вказати як попередні вер­шини, так і наступні (тобто щоб ці множини вершин не перетиналися). Дерево гри закінчується термінальними вершинами, які вже не мають «на­ступних вершин».

23. Визначення оптимальних стратегій динамічних ігор.

Для визначення оптимальних стратегій динамічних ігор застосовується так званий метод зворотної індукції. Опишемо цей метод.

Розглянемо сукупність дій, які може виконати певний гравець, який знаходиться в заданій вершині дерева гри. Рішення, яке приймає гравець в цій вершині, не залежить від взаємодії з іншими гравцями (це справедли­во тільки і тільки для гри із досконалою інформацією!), і тому гравець мо­же однозначно вибрати своє оптимальне рішення, а тепер, знаюче це рі­шення гравця, ми можемо розглянути ситуацію в «попередній» вершині (вже для іншого гравця). І так далі.

Очевидно, що такий розгляд повинен починатися «з кінця», від коне­чних (термінальних) вершин для заданої динамічної гри.

24. Гра з повною та неповною інформацією.

Гра називається грою із досконалою інформацією у тому випадку, коли кожен гравець може однозначно ви­значити своє місце в часовому розгортанню гри (тобто коли відсутні одно­часні ходи і коли всі гравці спостерігають за «ходами Природи»).

Гра із недосконалою інформацією має місце в тому випадку, коли порушуються умови наведеного вище визначення.

25. Гра в розгорнутій формі.

Гра в розгорнутій формі представляється увигляді описання окремих ходів і їх послідовностей, а не стратегій. Для цієї мети часто застосовуються мережеві структури - графи, причому переважно - "вихідні" дерева.

Вихідним деревом називають зв'язний спрямований (орієнтований) граф з єдиним витоком ("коренем"), якщо в графі немає циклів, і кожен вузол має єдиного безпосереднього попередника.

Граф гри ми будемо позначати Г(G), точки вибору учасників будуть "вузлами", а ходи - "дугами" графа. Кожному кінцевому вузлу, тобто (фінальній) "вершині", або "результату" гри, приписуються деякі виграші всіх учасників. Тим самим, граф гри задає фізичну і цільову структури гри, а інформаційна структура гри відбивається "інформаційними множинами".

Інформаційна множина або інформаційна позиція гри є кілька вузлів (фізичних позицій) графа гри, відповідних певному ходу одного учасника, який не може розрізняти між ними (не знає, в якому вузлі він знаходиться).