Лаба1.1

Новокузнецкий институт (филиал)

федерального государственного бюджетного образовательного учреждения

высшего профессионального образования

«Кемеровский государственный университет»

Отчет о лабораторной работе №1.1

«Движение с постоянным ускорением».

Выполнил: студент гр. ПМИ-101

Черепанов Данил Владимирович

Принял: кандидат тех. наук,

доцент кафедры экологии и естествознания Чмелева К. В.

г. Новокузнецк

2011 г.

Лабораторная работа №1.1.

«Движение с равномерным ускорением».

Цель работы:

-Знакомство с применением физической модели МАТЕРИАЛЬНАЯ ТОЧКА (МТ).

-Исследование движения МТ с постоянным ускорением.

- Экспериментальное определение ускорения свободного падения на поверхности Земли.

Краткая теория:

МАТЕРИАЛЬНАЯ ТОЧКА- это объект, не имеющий размеров, но обладающий другими характеристиками реального тела.

ПОЛОЖЕНИЕ МТ- это координата, которую имеет МТ в данный момент времени. Математическое описание положения МТ - ее радиус-вектор .

МЕХАНИЧЕСКОЕ ДВИЖЕНИЕ -это изменение положения тела в пространстве со временем. Закон движения - это функция .

СКОРОСТЬ - векторная кинематическая характеристика движения, показывающая быстроту и направление движения. .

УСКОРЕНИЕ -это векторная кинематическая характеристика движения, показывающая быстроту и направление изменения скорости. .

ТРАЕКТОРИЯ -это совокупность точек, которые последовательно проходит МТ при ее движении. В каждой точке вектор скорости направлен по касательной к траектории.

Для движения с постоянным ускорением закон движения , где - начальное положение и - начальная скорость МТ. Закон скорости: .

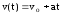При свободном движении тела вблизи поверхности Земли - ускорению свободного падения.

ТАНГЕНЦИАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется величина скорости ; оно направлено по касательной к траектории.

НОРМАЛЬНОЕ УСКОРЕНИЕ – показывает, как быстро меняется направление вектора скорост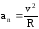и (R – радиус кривизны траектории). Оно перпендикулярно касательной.

Полное ускорение определяется по теореме Пифагора: .

Ход работы:

Начальная высота h=10 м

Начальный угол =60⁰

Номер измерения	Траектор. 1 vo = 15 (м/с)			Траектор. 2 vo = 17 (м/с)			Траектор. 3 vo = 19 (м/с)			Траектор. 4 vo = 22 (м/с)			Траектор. 5 vo = 25 (м/с)
	ymax	ymax	ymax		ymax	ymax		ymax	ymax		ymax	ymax		ymax
1	18,6	0	21		0	23,8		0	28,4		0	33,9		0
2	18,6	0	21		0	23,8		0	28,4		0	33,9		0
3	18,6	0	21		0	23,8		0	28,4		0	33,9		0
4	18,6	0	21		0	23,8		0	28,4		0	33,9		0
5	18,6	0	21		0	23,8		0	28,4		0	33,9		0
<ymax>	18,6			21			23,8			28,4			33,9
Абс.ош.	0			0			0			0			0

График зависимости средних значений вертикальной координаты точки максимального подъема от квадрата начальной скорости:

Выведем формулу для y_max максимальной высоты подъема тела:

Из формулы x=x₀+V₀t+(at²)/2 по аналогии получаем:

y_max=y₀+V₀t+(gt²)/2.

Т. к. в начальный момент времени V₀=0, то формула приобретает вид:

y_max=y₀+(gt²)/2.

Преобразуем формулу: gt²/2=y-y₀

gt²=2(y-y₀)

Отсюда получаем: t=

Подставляем данное выражение в исходную формулу:

y=y₀+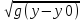

Вычисление значения ускорения свободного падения g:

g₁= 0,5*sin²(60⁰)*(625-289) = 1008 = 9,76 м/с² (33,9-21) 103,2

g₂= 9,8 м/с²

g₃= 10 м/с²

g₄= 9,9 м/с²

g₅= 9,8 м/с²

g_ср= (9,76+9,8+10+9,9+9,8)/5= 9,8 м/с²

Δ (g_ср)= 0.

Полученный экспериментально график зависимости значений вертикальной координаты точки максимального подъема

от квадрата начальной скорости имеет вид непрерывной ломаной кривой

и качественно совпадает с теоретической зависимостью данных характеристик, имеющей вид y=y₀+ .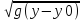

Вывод: Таким образом, мы исследовали движение материальной точки с постоянным ускорением и экспериментально определили ускорение свободного падения на поверхности Земли. Полученные значения полностью совпадают с исходными данными.