Лекции по дискретной математике / Матрицы бинарных отношений

Матрицы бинарных отношений

Рассмотрим два конечных множества A ={a₁,a₂,…,a_m} и B={b₁,b₂,…,b_n} и бинарное отношение . Определим матрицу размера m×n бинарного отношения Р по следующему правилу:

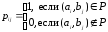
Полученная матрица содержит полную информацию о связях между элементами.

Любая матрица, состоящая из 0 и 1, является матрицей некоторого бинарного отношения.

ПРИМЕР 1. Матрица бинарного отношения , A={1,2,3}, заданного

на рисунке имеет вид

Основные свойства матриц бинарных отношений:

1. Если то и 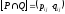, где сложение осуществляется по правилам 0+0=0, 1+1=0+1=1+0=1, а умножение – обычным способом.

Итак,

2. Матрица получается перемножением соответствующих элементов из и : .

3. Если , то 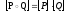, где умножение матриц производится по обычному правилу умножения матриц, но произведение и сумма элементов – по определённым в свойстве 1 правилам.

4. Матрица обратного отношения Р^-1 равна транспонированной матрице отношения Р: .

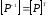5. Если , то .

6. Матрица тождественного отношения id_A единична:

ПРИМЕР 2. Пусть - матрицы отношений P и Q. Тогда

ПРИМЕР 3. Если 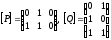, то

Рассмотрим свойства отношений на языке матриц.

Пусть Р – бинарное отношение на множестве . Отношение Р:

• рефлексивно, если на главной диагонали матрицы отношения расположены только единицы;

• симметрично, если матрица симметрична относительно главной диагонали;

• антисимметрично, если в матрице все элементы вне главной диагонали являются нулевыми;

• транзитивно, если выполнено соотношение .

ПРИМЕР 4. Проверим, какими свойствами обладает отношение 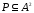, А={1,2,3}, изображённое на рисунке.

Составим матрицу отношения Р:

Так как в матрице на главной диагонали имеются нулевые элементы, отношение Р не рефлексивно.

Несимметричность матрицы означает, что отношение Р не симметрично.

Для проверки антисимметричности вычислим матрицу .

Поскольку в полученной матрице все элементы, стоящие вне главной диагонали, нулевые, отношение Р антисимметрично.

Так как (проверьте!), то , то есть Р является транзитивным отношением.