Сбалансированные деревья

Анализ задачи поиска по дереву с включениями узлов показывает, что эффективность алгоритма зависит от формы, которую принимает растущее дерево. Легко найти наихудший случай: ключи поступают в порядке возрастания, и дерево оказывается полностью вырожденным, то есть превращается в линейный список. В этом случае среднее число сравнений ключей равно N/2. Наилучший вариант получается, если дерево строится идеально сбалансированным, в этом случае среднее число сравнения равно logN.

Н. Вирт показал, что строя идеально сбалансированное дерево, следует ожидать выигрыш в длине пути поиска в среднем не более 39%. Эта цифра достаточно низка, и в большинстве случаев не оправдывает затрат на восстановление идеальной сбалансированности дерева. Попробуем добиться эффективности менее дорогим способом, введя менее строгое понятие сбалансированности дерева.

Критерий сбалансированности дерева (Адельсон-Вельский, Ландис, 1962):

Дерево является сбалансированным тогда и только тогда, когда для каждого его узла высота его двух поддеревьев различается не более чем на 1.

Дерево, удовлетворяющее этому критерию, называют АВЛ-деревом или сбалансированным деревом. Понятно, что идеально сбалансированное дерево является АВЛ-деревом. Введем понятие баланса узла, как разность между высотой его правого и левого поддерева:

Bal = Hr – Hl.

Тогда критерий сбалансированности формулируется следующим образом:

Дерево является сбалансированным тогда и только тогда, когда для каждого его узла bal  [-1, 1].

Рассмотрим, что происходит со сбалансированным деревом при добавлении узла. Предположим, что узел добавляется слева. Возможны три случая.

1. Баланс узла = 0. После добавления высота дерева меняется, но критерий сбалансированности дерева не нарушается, так как баланс узла становится равным –1.

2. Баланс узла = +1. После добавления высота дерева не меняется, критерий сбалансированности дерева не нарушается, баланс узла становится равным 0.

3. Баланс узла = -1. После добавления высота дерева меняется, критерий сбалансированности дерева нарушается, требуется перестройка дерева.

Аналогичная ситуация при добавлении узла справа.

1. Баланс узла = 0. После добавления высота дерева меняется, но критерий сбалансированности дерева не нарушается, так как баланс узла становится равным +1.

2. Баланс узла = -1. После добавления высота дерева не меняется, критерий сбалансированности дерева не нарушается, баланс узла становится равным 0.

3. Баланс узла = +1. После добавления высота дерева меняется, критерий сбалансированности дерева нарушается, требуется перестройка дерева.

Таким образом, имеем два вида преобразований дерева LL и LR. Рассмотрим в общем случае: LL

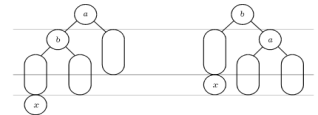
Пусть указатель T показывает на узел a, P1 на его левое поддерево b. Тогда преобразование LL сводится к следующим операциям:

T^.left:=P1^.right;

P1^.right:=T;

T:=P1;

После преобразования LL баланс узла a равен 0, баланс узла b равен 0.В случае преобразования LR реорганизация идет более сложная.

Пусть указатель T показывает на узел a, P1 - на его левое поддерево b, P2 – на правое поддерево дерева b (узел c). Тогда преобразование LR сводится к следующим операциям:

P2:=P1^.right;

P1^.right:=P2^.left;

P2^.left:=P1;

T^.left:=P2^.right;

P2^.right:=T;

T:=P2;

После преобразования LR баланс узла c равен 0, баланс узла b равен 0 или –1, баланс узла a равен 0 или +1.

Добавление справа – зеркальная симметрия. RR-поворот и RL-поворот.

Удаление из сбалансированного дерева

Простыми случаями являются удаление терминального узла или узла с одним поддеревом. Узел с двумя поддеревьями удаляется заменой на самый правый узел левого поддерева. Следует контролировать при удалении узла высоту поддерева, в случае ее уменьшения рассматривается вопрос о балансировке.

Операция вставки вызывает самое большее один поворот. Операция удаления может вызвать поворот в каждом узле вдоль пути поиска, то есть порядка log N поворотов.

Алгоритм поиска – такой же как в бинарном дереве поиска.

Временная сложность поиска: O(log n) в любом случае.