29. Линейные и нелинейные структуры данных (стеки, деревья, очереди). Определения, основные операции, реализация.

Программы представляют собой конкретные формулировки абстрактных алгоритмов, основанные на конкретном языке и структурах данных. Алгоритмы и структуры данных всегда используются совместно: выбор алгоритма существенно зависит от структуры данных и наоборот (хотя интуитивно понятно, что структуры данных - первичны).

Алгоритм – способ решения вычислительной задачи. Алгоритмы всегда абстрактны – они могут быть реализованы на конкретном языке, и на конкретной машине. Основные характеристики алгоритмов – эффективность, надежность.

Тип данных – множество значений и операций с ними.

Абстрактный тип данных – математическая модель данных и совокупность операций, определенных в рамках этой модели.

Структура данных:

1. Совокупность операций с данными (АТД).

2. Структура хранения данных в памяти компьютера.

3. Реализация каждой операции.

Абстрактные структуры данных предназначены для удобного хранения и доступа к информации. Они предоставляют удобный интерфейс для типичных операций с хранимыми объектами, скрывая детали реализации от пользователя. К классическим, наиболее распространенным структурам данных относятся массивы, записи, связанные списки, стеки, очереди, деревья.

ЛИНЕЙНЫЕ СТРУКТУРЫ

Массивы представляют собой смежные ячейки памяти, начиная с начального адреса массива и до последней ячейки памяти массива. Доступ к каждой ячейке памяти осуществляется по его индексу. С помощью индекса вычисляется адрес нужной ячейки по формуле:

<адрес элемента> = <начальный адрес массива>+<индекс>*<длина типа данных>

Индекс массива

Индекс - порядковый номер элемента массива в отведенной для него области памяти. Операция нахождения значения ячейки массива по его индексу называется индексированием.

Максимальный индекс массива определяется следующими способами:

1. Явное указание максимальных индексов целыми константами:

const short MAXNUMBER = 8;

char str[7];

short nIndexes[MAXNUMBER];

2. Определение элементов массива по количеству заранее предопределенных для него значений:

char str[] = "Привет!";

short nIndexes[] = {5, 4, 6, 8, 7, 3, 1, 2};

В C++ массивы "основаны на нуле" - первый элемент - элемент [0], в Delphi начало массива в элементе 1... но не всегда.В Delphi встречаются компоненты и объекты "основаные на нуле" наподобие С++. 

НЕЛИНЕЙНЫЕ СТРУКТУРЫ

Нелинейные — структуры данных, в которых переход от одного элемента данных к другому может зависеть от выполнения некоторого логического условия, т.е.могут использоваться условные связи элементов. Порядок следования элементов таких структур может не соответствовать порядку расположения элементов в памяти.

СВЯЗАННЫЕ СПИСКИ

АТД линейный список (linear list) — последовательность элементов a₁, a₂, …, a_N, (N ≥ 0), все элементы которой имеют один базовый тип.

Списком называется упорядоченное множество, состоящее из переменного числа элементов, к которым применимы операции включения, исключения. Список, отражающий отношения соседства между элементами, называется линейным. Длина списка равна числу элементов, содержащихся в списке, список нулевой длины называется пустым списком.

Связанные списки, определенны как стандартные структуры в некоторых языках программирования (например, в Лиспе).

Связанные списки имеют два преимущества перед массивами:

• они динамично могут изменять свои размеры,

• позволяют легко реорганизовать порядок элементов, добавлять и удалять элементы, путем редактирования небольшого числа ссылок.

Существует несколько видов связанных списков, в зависимости от ссылок:

• ОДНОСВЯЗНЫЕ

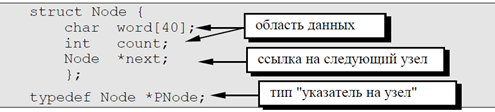
Каждый элемент содержит также ссылку на следующий за ним элемент. У последнего NULL. Чтобы не потерять список, мы должны хранить адрес его первого узла – он называется "головой" списка. В программе надо объявить два новых типа данных - узел списка Node и указатель на него PNode.

Операции со списком

Создание узла

После этого узел надо добавить к списку.

Добавление узла в начало списка

Void AddFirst(PNode NewNode)

{NewNode->Next=Head;

Head=NewNode;}

Проход по списку

Добавление узла после заданного

Void AddAfter(PNode p,PNode NewNode)

{NewNode->next=p->next;

p->next=NewNode; }

\Удаление узла

Время вставки O(1). Время доступа к элементу O(N).

ОЧЕРЕДИ С ПРИОРИТЕТАМИ:

АТД очередь с приоритетами (priority queue). Элементы очереди имеют приоритеты и обслуживаются по принципу их важности. Очереди с приоритетным включение и удалением (одна из операций выполняется за время O(N), другая O(1)). Одна из наиболее эффективных реализаций, при которой обе операции выполняются за время O(logN) предложена Д. Уильямсом на базе пирамиды.

ДЕКИ

Дек (deque – double-ended queue)— это линейный список, в котором все операции вставки и удаления выполняются на обоих концах списка. Основные операции: Вставка/Удаление элемента в левый/правый конец.

Физическая структура дека в статической памяти идентична структуре кольцевой очереди. Динамическая реализация является очевидным объединением стека и очереди. Примером дека может быть некий терминал, в который вводятся команды, каждая из которых выполняется какое-то время. Если ввести следующую команду, не дождавшись, пока закончится выполнение предыдущей, то она встанет в очередь и начнет выполняться, как только освободится терминал. Это FIFO очередь. Если же дополнительно ввести операцию отмены последней введенной команды, то получается дек.

ДЕРЕВЬЯ

Одна из наиболее распространенных динамических структур в вычислительных алгоритмах. Деревья впервые появились для манипуляции с формулами при развитии компиляторов в 1951, 1952-54гг.

Определим дерево, как конечное множество Т, которое либо пусто, либо в нем имеется один специально обозначенный узел, называемый корнем, а все остальные узлы содержатся в непересекающихся множествах T₁, T₂,..., T_m, каждое из которых является деревом. Деревья T₁, T₂,..., T_m называют поддеревьями данного корня. Или – совокупность элементов, которые называются узлами и отношений, образующих иерархическую структуру узлов.

Основной характеристикой этих динамических структур является рекурсивность. Поэтому рекурсивные алгоритмы обработки деревьев являются наиболее уместными.

Способы изображения деревьев

1. вложенные множества

2. вложенные скобки (a(b(d)) (c (e)(f (g)(h)(i)) ))

3. В виде оглавления

Основные определения

1. Степень узла - число поддеревьев, выходящих из этого узла.

2. Степень дерева - максимальная из всех степеней узлов.

3. Лист (терминальный узел, внешний узел) - узел степени 0.

4. Уровень узла - количество узлов на 1 меньше на пути от корня до этого элемента.

5. Высота дерева - максимальный из уровней узлов

6. Длина пути дерева – сумма уровней всех узлов

7. Лес – множество, состоящее из некоторого числа непересекающихся деревьев.

8. Упорядоченное дерево - дерево, у которого важен порядок следования поддеревьев.

9. Бинарное дерево - упорядоченное дерево степени 2.

10. Деревья, имеющие степень больше 2, называются m-арными деревьями.

11. Полное дерево – дерево, в котором внутренние узлы полностью заполняют каждый его уровень, за исключением возможно последнего.

12. Бинарное дерево идеально сбалансировано, если для каждого узла количество узлов в левом и правом поддереве различаются не более чем на 1.

13. Расширенное дерево:

Любое упорядоченное дерево можно преобразовать в бинарное!

Математические свойства бинарных деревьев.

Свойство 1. Бинарное дерево с N внутренними узлами имеет N + 1 внешний узел.

Свойство 2. Бинарное дерево с N внутренними узлами имеет 2N связей: N - 1 связей с внутренними узлами и N + 1 связей с внешними узлами.

Свойство 3. Длина внутреннего пути любого бинарного дерева, имеющего N внутренних узлов, равна сумме длин внутренних путей поддеревьев корня плюс N - 1.

Свойство 4. Длина внешнего пути любого бинарного дерева, имеющего N внутренних узлов, равна сумме длин внешних путей поддеревьев корня плюс N + 1.

Свойство 5. Длина внешнего пути любого бинарного дерева, имеющего N внутренних узлов, на 2N больше длины внутреннего пути.

Свойство 6. Высота бинарного дерева с N внутренними узлами не меньше log₂ N и не больше N – 1.