
ТФКП + Механика сплошных сред / Функции комплексного переменного
.docxФункции комплексного переменного
Говорят,
что в области
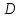 определена функция комплексного
переменного
определена функция комплексного
переменного
 ,
если каждой точке
,
если каждой точке
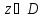 поставлено в соответствие одно
(однозначная функция) или несколько
(многозначная функция) значений
поставлено в соответствие одно
(однозначная функция) или несколько
(многозначная функция) значений
 .
.
Таким
образом, функция
 осуществляет отображение точек
комплексной плоскости
осуществляет отображение точек
комплексной плоскости
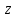 на соответствующие точки комплексной
плоскости
на соответствующие точки комплексной
плоскости
 .
.
Пусть
 и
и
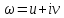 .
Тогда зависимость
.
Тогда зависимость
 между комплексной функцией
между комплексной функцией
 и комплексной переменной
и комплексной переменной
 может быть описана с помощью двух
действительных функций
может быть описана с помощью двух
действительных функций
 и
и
 действительных переменных
действительных переменных
 и
и

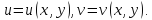
Пример
1.
Пусть
 .
.
Полагая
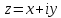 ,
,
 ,
получим
,
получим


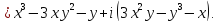
Следовательно,
равенство
 равносильно двум равенствам
равносильно двум равенствам
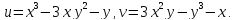
Пусть
в плоскости
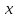 кривая задана уравнением
кривая задана уравнением
 .
Чтобы найти уравнение образа
.
Чтобы найти уравнение образа
 этой кривой в плоскости
этой кривой в плоскости
 при отображении помощью функции
при отображении помощью функции
 ,
нужно исключить
,
нужно исключить
 и
и
 из уравнений
из уравнений

Если кривая задана параметрическими уравнениями
 или
или
 ,
,
то
параметрические уравнения ее образа
при отображении
 будут
будут

Пример
2.
В какую кривую отображается единичная
окружность
 с помощью функции
с помощью функции
 ?
?
Так
как по условию
 ,
то
,
то
 .
Итак, образом окружности
.
Итак, образом окружности
 в плоскости
в плоскости
 является окружность
является окружность
 в плоскости
в плоскости
 ,
проходимая дважды. Это следует из того,
что поскольку
,
проходимая дважды. Это следует из того,
что поскольку
 ,
то
,
то
 ,
так что когда точка
,
так что когда точка
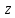 описывает полную окружность
описывает полную окружность
 ,
то ее образ описывает окружность
,
то ее образ описывает окружность
 дважды.
дважды.
Пример
3.
Найти образ окружности
 при
отображении
при
отображении
 .
.
Пусть
 .
Данное уравнение окружности можно
записать в виде
.
Данное уравнение окружности можно
записать в виде

Отделим
действительную и мнимую части функции
 .
Имеем
.
Имеем

Отсюда

Подставляя
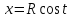 ,
,
 в
в
 и
и
 ,
получим параметрические уравнения
образа окружности
,
получим параметрические уравнения
образа окружности

или
 .
.
Итак,
образ есть единичная окружность,
проходимая дважды, что следует из того,
что
 и формул (*).
и формул (*).
Основные элементарные функции комплексного переменного
-
Дробно-рациональная функция

в частности, рациональной функцией является многочлен
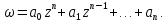
-
Показательная функция
 определяется как сумма абсолютно
сходящегося во всей комплексной
плоскости степенного ряда
определяется как сумма абсолютно
сходящегося во всей комплексной
плоскости степенного ряда

Показательная функция обладает следующими свойствами:
а)
 ,
где
,
где
 и
и
 – любые комплексные величины;
– любые комплексные величины;
б)
 ,
т.е.
,
т.е.
 является периодической функцией с
периодом
является периодической функцией с
периодом
 .
.
-
Тригонометрические функции
 и
и
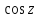 определяется степенными рядами
определяется степенными рядами


абсолютно
сходящимися при любом комплексном
значении
 .
Функции
.
Функции
 и
и
 – периодические с действительным
периодом
– периодические с действительным
периодом
 и имеют только действительные нули
и имеют только действительные нули
 и
и
 соответственно, где
соответственно, где
 .
.
Для
функций
 ,
,
 и
и
 имеют место формулы Эйлера
имеют место формулы Эйлера

откуда

Функции
 и
и
 определяются равенствами
определяются равенствами

Для тригонометрических функций остаются в силе все формулы тригонометрии.
-
Гиперболические функции
 ,
,
 ,
,
 ,
,
 определяется равенствами
определяется равенствами


-
Тригонометрические и гиперболические функции связаны между собой следующими соотношениями:




-
Логарифмическая функция
 ,
где
,
где
 ,
определяется как функция, обратная
показательной, причем
,
определяется как функция, обратная
показательной, причем

Эта
функция является многозначной. Главным
значением
 называется то значение, которое получается
при
называется то значение, которое получается
при
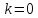 ;
оно обозначается
;
оно обозначается
 :
:

Очевидно, что
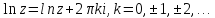
Справедливы следующие соотношения:

-
Обратные тригонометрические функции
 ,
,
 ,
,
 ,
,
 определяются как функции, обратные
соответственно к функциям
определяются как функции, обратные
соответственно к функциям
 ,
,
 ,
,
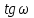 ,
,
 .
.
Например,
если
 ,
то
,
то
 называется арксинусом числа
называется арксинусом числа
 и обозначается
и обозначается
 .
.
Все эти функции являются многозначными и выражаются через логарифмические функции




Главные
значения обратных тригонометрических
функций
 ,
,
 ,
,
 ,
,
 получаются, если брать главные значения
соответствующих логарифмических
функций.
получаются, если брать главные значения
соответствующих логарифмических
функций.
-
Общая степенная функция
 ,
где
,
где
 – любое комплексное число, определяется
равенством
– любое комплексное число, определяется
равенством

Эта функция, вообще говоря многозначная; ее главное значение равно
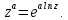
-
Общая показательная функция
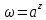 (
( – любое комплексное число) определяется
равенством
– любое комплексное число) определяется
равенством

Главное
значение этой многозначной функции

Пример
4.
Найти значение модуля функции
 в точке
в точке
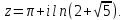
Пусть
 .
Тогда
.
Тогда

Модуль
функции
 равен
равен


Полагая
 ,
найдем
,
найдем

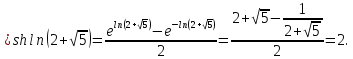
Этот пример показывает, что тригонометрическая функция в комплексной области может принимать значения, по модулю большие единицы.
Пример
5.
Записать в алгебраической форме
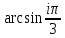 .
.
Полагая
в формуле (7)
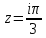 ,
получим
,
получим

Отсюда



и

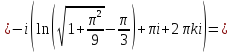

Пример
6.
Записать в алгебраической форме
 .
.
Полагая
в формуле (9)
 ,
получим
,
получим

Далее

Окончательно
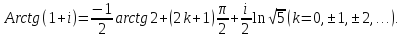
Пример
7.
Решить уравнение
 .
.
Задача
сводится к нахождению величины
 .
Воспользуемся формулой (7)
.
Воспользуемся формулой (7)
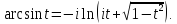
Будем иметь

Или,
учитывая то, что
 ,
получим
,
получим

Так как


то

где
 .
Следовательно,
.
Следовательно,

№1. Для следующих функций найти действительную и мнимую части:
а)
 ;
б)
;
б)
 .
.
№2. Найти образ данной точки при указанных отображениях
а)
 ;
б)
;
б)
 .
.
№3. Установить на какие линии плоскости отображаются с помощью функции следующие линии плоскости :
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
№4. Найти образы координатных осей и при следующих отображениях:
а)
 ;
б)
;
б)
 .
.
№5. Выделить действительную и мнимую части у следующих функций:
а)
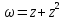 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 ;
д)
;
д)
 .
.
№6. Найти значение модуля и главное значение аргумента данных функций в указанных точках:
а)
 ;
;
б)
 ;
в)
;
в)
 .
.
№7. Найти:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 .
.
№8. Записать в алгебраической форме следующие комплексные числа:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.
№9. Решить следующие уравнения:
а)
 ;
б)
;
б)
 ;
в)
;
в)
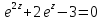 ;
г)
;
г)
 .
.
