Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема3-9

3.9. Нагрев или охлаждение неограниченного полого цилиндра.

Неограниченный полый цилиндр - это, другими словами, труба большой дли­ны, характеризующаяся двумя радиусами: R₁ (внутренний радиус трубы) и R₂ - внешний радиус. В двух задачах, которые мы рассмотрим ниже, требуется най­ти рас­пре­де­ле­ние тем­пе­ра­ту­ры внутри стенки трубы, т.е. в области в любой момент времени: T(r,t) в области . Бу­дем ис­поль­зо­вать следующие обозначения: число Фурье (безразмерное вре­мя) Fo = at/(R₂ - R₁)², критерий Био Bi = (R₂ - R₁)/, где , a - коэффициенты тепло- и тем­пе­ра­ту­­­ро­про­вод­ности материала трубы соответственно, t - обычное время (в секундах), от­но­ше­ние радиусов k = R₂/R₁ > 1. Подробнее о числах Фурье и Био см. ниже в разделе 6 "Безразмерные пара­метры тепломассообмена".

Задача 1. Неограниченный полый цилиндр (труба большой длины) на­хо­дит­ся в теп­ло­вом равновесии с окружающей средой, имеющей температуру T_c, т.е. начальная тем­пе­ра­ту­ра трубы T₀ = T_c. В мо­мен­т времени t = 0 внутри ци­лин­дра начинает работать источник теп­ла с постоянной мощностью, соз­да­ю­щий тепловой поток с плотностью q через внут­рен­нюю поверхность трубы. Тру­ба начинает нагреваться, и возникает тепло­обмен между ее внеш­ней по­верх­ностью и окружающей средой; коэффициент теплообмена . Требуется най­ти рас­пре­де­ле­ние тем­пе­ра­ту­ры по толщине стенки трубы в любой момент вре­мени: T(r,t).

Приближенное решение этой задачи, пригодное для практи­ческих рас­че­тов, имеет вид:

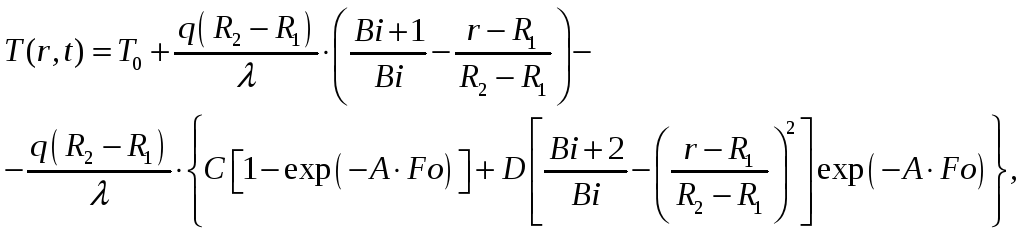(3.9.1)

где вспомогательные параметры A, C, D вычисляется по формулам:

, ,

.

Формула (3.9.1) пригодна как для нагрева, так и для охлаждения. Точ­ность этой формулы зависит от критерия Био и числа Фурье: при увеличении критерия Био и умень­шении числа Фурье погрешность воз­растает, но не превышает 6% . При Bi < 5 и Fo > 0.1 погрешность состав­ля­ет менее 3%.

Задача 2. Начальная тем­пе­ра­ту­ра трубы не равна температуре окру­жа­ю­щей среды: T₀  T_c. Внутренняя поверхность трубы теплоизолирована, а на вне­ш­ней поверхности происходит теплообмен окружающей средой с коэф­фи­ци­ен­том теплообмена . Вследствие этого труба остывает, если ее начальная тем­пе­ра­тура T₀ была больше температуры T_c, или нагревается, если T₀ < T_c. Требуется найти рас­пре­де­ле­ние тем­пе­ра­ту­ры по толщине стенки трубы в любой момент времени: T(r,t).

Приближенное решение этой задачи, пригодное для практи­ческих расчетов, имеет вид:

, (3.9.2)

где вспомогательные параметры A и D вычисляется по формулам:

, .

В пределе при k   (R₂ = const, R₁  0) формула (3.9.2) совпадает с формулой (3.8.1) для распределения температуры в сплошном цилиндре при постоянных граничных условиях третьего рода, как и должно быть.