Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема2-1

ТЕМА 2.СТАЦИОНАРНЫЕ ЗАДАЧИ ТЕОРИИ ТЕПЛОПРОВОДНОСТИ.

2.1.Стационарное температурное поле в пластине. Простейшие тепло­тех­ни­чес­кие формулы.

2.1.1.Постановка задачи и общее решение.

Одной из простейших задач теории теплопроводности яв­ля­ется задача об определении одномерного стационарного тем­пе­ра­турного поля и теп­ло­во­го потока в декартовых ко­ор­ди­натах. Рас­смотрим плоскую стенку (на­при­мер, стену ка­ко­го-либо зда­ния или сооружения) или плоскую плас­ти­ну из од­нородного ма­те­риала толщины L. Пусть на одной из сто­рон этой плас­ти­ны под­держивается температура T₁, а на дру­гой T₂ (см. ри­сунок). Бу­дем счи­тать, что высота и ширина пластины велики по срав­не­нию с ее тол­щи­ной L, и тем­пе­ра­ту­ра в этих направлениях практически не меняется. Для этих ус­ло­вий

; ,

и уравнение теплопроводности принимает простейший вид (1.2.4) при f = 0. Да­лее, условие ста­ци­о­нар­нос­ти означает, что T/t = 0, поэтому

, или ,

т.к. температура зависит от единственной переменной x. Очевидным решением это­го уравнения является

, (2.1.1)

T = C₁x + C₂, (2.1.2)

где C₁ и C₂ - константы интегрирования, которые должны быть определены из гра­ничных ус­ло­вий. Из по­лу­чен­ного общего решения видно, что в плоской пла­с­тине без внутренних источников теп­ла ста­ционарное рас­пределение тем­пе­ра­ту­ры при граничных условиях любого типа является ли­ней­ным.

Решение данной простой задачи можно получить и непосредственно из за­кона Фурье (1.1.4), не обращаясь к урав­нению теплопроводности. Дейст­ви­тель­но, из условия стационарности следует, что плотность теплового потока q при любом значении x должна быть одной и той же, иначе в каких-то точках теп­ло накапливалось бы и тем­пе­ра­ту­ра ме­ня­лась бы со временем. Отсюда на­хо­дим: dT/dx = -q/ = const = C₁, т.е. формулу (2.1.1), интегрируя которую по­лу­ча­ем формулу (2.1.2).

2.1.2.Граничные условия 1-го и 2-го рода.

Если, как сказано выше, на поверхности плас­ти­ны x = 0 поддерживается температура T₁, а на поверхности x = L - температура T₂, т.е. заданы условия первого рода на обеих поверхностях, то для определения констант интегрирования имеем:

T₁ = C₂,, T₂ = C₁ L + C₂ ,

откуда C₁ = (T₂ - T₁)/L, и

, (2.1.3)

а плотность теплового потока

. (2.1.4)

Последнюю формулу в теплотехнике принято записывать в виде:

. (2.1.5)

Эта формула аналогична закону Ома для электрического тока (сила тока рав­на на­пря­же­нию, деленному на сопротивление данного участка проводника), по­этому разность T₁ - T₂ на­зы­ва­ют тем­пературным напряжением, или тем­пе­ра­турным напором, величину L/ - теп­ло­вым или тер­ми­ческим со­про­тив­ле­ни­ем, а обратную величину /L - тепловой про­во­ди­мостью пла­с­ти­ны.

Если на границе х = 0 задано условие второго рода:

, (2.1.6)

где q - плотность мощности подводимого к пластине теплового потока, а на границе х = L, как и рань­ше, дано условие первого рода: Т_x=L = T₂, то получаем следующие значения констант:

C₁ = -q/, C₂ = T₂ + qL/,

таким образом,

. (2.1.7)

В частности, температура на границе х = 0 в этом случае равна:

. (2.1.8)

2.1.3.Граничные условия 3-го рода.

Пусть на обеих поверхностях пластины заданы условия теплообмена с ок­ру­жающей средой в виде:

, (2.1.9)

, (2.1.10)

где T₀₁ и T₀₂ - температура окружающей среды слева и справа от пластины (на­при­мер, тем­пе­ра­ту­ра воздуха в помещении и на улице); ₁ и ₂ - со­от­вет­ст­ву­ю­щие коэффициенты теплообмена.

Подставляя сюда из формул (2.1.1) и (2.1.2) значения dT/dx = C₁, T₁ = C₂, T₂ = C₁L + C₂, получаем систему уравнений относительно констант C₁ и C₂:

-C₁ = ₁ (T₀₁ - C₂),

C₁ = ₂ (T₀₂ - C₁L - C₂),

решая которую находим:

, .

Таким образом, распределение температуры внутри пластины имеет вид:

, (2.1.11)

плотность теплового потока

, (2.1.12)

а тепловое сопротивление

. (2.1.13)

2.1.4. Граничные условия 4-го рода. Поток тепла через многослойную пластину.

Многослойные конструкции - наиболее распространенный тип ограж­де­ний. Например, сте­ны жилых домов на основном кирпичном слое имеют внут­рен­нюю штукатурку и внешнюю об­ли­цов­ку; во многих технических уст­ройст­вах применяются специальные тепло­изо­ля­ци­он­ные по­кры­тия и т.д.

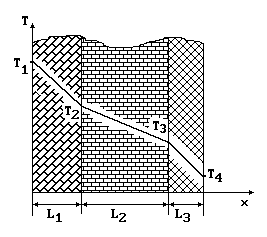Рассмотрим плоскую стенку, состоящую из нес­коль­ких (на­при­мер, из трех) разнородных, плот­но при­ле­гающих друг к другу слоев, имеющих толщину L₁, L₂, L₃ и теплопроводность ₁, ₂, ₃ со­от­вет­ст­вен­но (см. рисунок). Пусть температуры наружных по­верх­нос­­тей стен­ки T₁ и T₄ заданы. Соприкасающиеся по­верх­ности слоев имеют тем­пе­ра­ту­ры T₂ и T₃, но значения их заранее не­из­вест­ны. Согласно ус­ловиям (1.3.5) и (1.3.6) для сопряженной задачи, тем­пе­ратура и теп­­ловой поток при переходе через соприкасающиеся по­верх­ности ме­­няются не­прерывно, в стационарном режиме плотность теп­лового по­­тока q, про­хо­дя­ще­го через каждый слой стен­ки, оди­на­ко­ва по­э­то­му для каждого слоя стенки можно написать:

, , , (2.1.14)

откуда

, (2.1.15)

, (2.1.16)

. (2.1.17)

Складывая (2.1.15) - (2.1.17), находим:

.

Отсюда получаем формулу для плотности теплового потока q, а затем из (2.1.14) определяем неизвестные температуры T₂ и T₃:

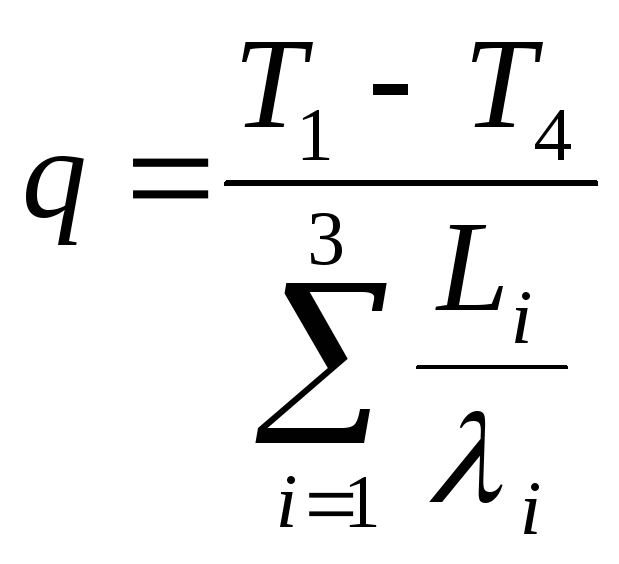, (2.1.18)

.

Формулу (2.1.18) легко обобщить на случай n-слойной стенки и объе­ди­нить с ре­зуль­та­том, полученным для граничных условий 3-го рода (с формулой (2.1.13)): для многослойной стен­ки, состоящей из пластин толщиной L_i с со­от­вет­с­твующими коэффициентами тепло­про­водности _i, тепловое со­про­тив­ле­ние определяется формулой:

. (2.1.19)