Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема3-3

3.3.Температурное поле непрерывного неподвижного точечного источ­ни­ка в неограниченной среде. Функция ошибок Гаусса (функция erf(x)).

Если в точ­ке с координатами x', y', z' в интервале времени от t' = 0 до t' = t ра­ботает источник тепла мощностью W, то температурное поле этого ис­точ­ни­ка, как указано выше, мо­жет быть найдено интегрированием фундаментального решения по t' от 0 до t (т.е. от момента включения до момента выключения источника). Поместим начало координат в точку, где находится источник теп­ла. Тогда x' = y' = z' = 0, и формула для температуры принимает вид:

, (3.3.1)

где r² = (x - x')² + (y - y')² + (z - z')² = x² + y² + z² - квадрат расстояния от источника до точки на­блю­де­ния.

Произведем в интеграле (3.3.1) замену переменных: r²/[4a(t - t')] = ². Тогда: (t - t')^3/2 = r³/(8a^3/2³), dt' = r²d/(2a³), пределы интегрирования: t' = 0  , t' = t   = , и фор­мула (3.3.1) принимает вид:

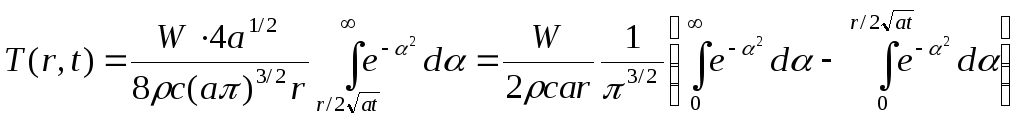. (3.3.2)

Первый интеграл, стоящий в скобках, известен из курса высшей математики:

(интеграл Пуассона),

а второй интеграл через элементарные функции не выражается и определяет специальную фун­к­цию, которая называется функцией ошибок Гаусса, или интегралом вероятностей, или фун­к­ци­ей эрфектум:

(3.3.3)

(читается "эрфектум" или сокращенно: "эрф"). Через эту функцию выражаются решения мно­гих задач в теории теплопроводности, да и в других областях физики она играет важную роль.

Из определения (3.3.3) видно, что erf(0) = 0, а erf() = 1, т.е. erf(x) - это мо­но­тон­но возрастающая функция, вид ко­то­рой изо­бражен на Рис.3.3. Функция erf(x) та­бу­ли­­ро­вана, и ее зна­чения приводят­ся в раз­лич­ных справочниках; в таблице 3.1 при­ве­де­ны несколько значений этой функции. В биб­ли­о­те­ках не­ко­торых языков программирова­ния имеются го­то­вые под­про­грам­мы для вы­чис­ления функции erf(x). Если готовой под­про­­грам­мы нет, функцию erf(x) можно вы­чис­лить с помощью степенного ряда. "Стан­дар­т­ное" раз­ло­жение этой функ­ции в сте­пен­ной ряд, которое обычно приводится в математи­чес­ких спра­воч­никах, име­ет вид:

. (3.3.4)

Э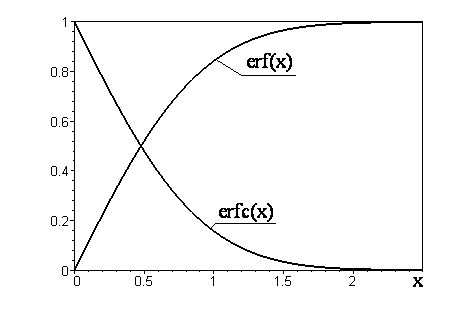тот ряд удобен для анализа свойств функции, но для практических расчетов он неудобен, т.к. яв­ляется знакопеременным, что при вычислениях приводит к потере точности. Более удобен сле­­дующий ряд:

, (3.3.5)

где

, .

С

Рис. 3.3.

помощью этого ряда легко соста­вить программу вычисления erf(x) на лю­бом языке про­грам­ми­рования и да­же на программируемом микро­каль­ку­ля­торе. Суммирование надо пре­кра­щать, ко­гда при добавлении оче­ред­но­го a_n-го слагаемого сумма перестанет ме­няться (будет до­стиг­ну­та "ма­шин­ная точность").

Если большой точности не требуется, то можно использовать приближенную фор­мулу:

erf(x)  [1 - exp(-4x²/)]^1/2. (3.3.6)

Формула (3.3.6) дает значения, абсолютная погрешность которых не более 6.310^-3, а отно­си­тель­ная погрешность не более 0.71%.

Иногда требуется определить erf(x) в области отрицательных значений x. Из формулы (3.3.3) очевидно, что erf(-x) = - erf(x).

Заметим, что хотя функция erf(x) не является "элементарной", с точки зре­ния ее свойств и способов вы­чис­ления она проще, чем многие "элементарные" функции, например, тригонометрические.

С функцией erf(x) связано еще несколько функций, часто встречающихся в тепло­фи­зи­чес­ких задачах. Это прежде всего дополнительный интеграл ве­ро­ят­ностей:

, (3.3.7)

который встречается настолько часто, что для него используется специальное обозначение: erfc(x) (сокращенно читается "эрфик"). Вид этой функции также приведен на рис.3.3.

Довольно часто функцию erf(x) приходится дифференцировать и ин­те­грировать. Из оп­ре­де­ления (3.3.3) следует, что

, (3.3.8)

а интеграл от erfc(x) (обозначается как ierfc(x)) равен:

. (3.3.9)

Вернемся к формуле (3.3.2). Замечая, что ca = , запишем эту формулу в виде:

. (3.3.10)

При t   значение функции  0,  1, и формула (3.3.10), как и должно быть, сов­па­да­ет с формулой для стационарного решения (если T₀ принять за на­ча­ло отсчета тем­пе­ра­ту­ры), т.к. при t   до­сти­га­ет­ся стационарное распределение тем­пе­ра­ту­ры в безграничной среде.

Таблица 3.1. Некоторые значения функции erf(x).

x	erf(x)	x	erf(x)	x	erf(x)	x	erf(x)	x		erf(x)
0.0	0.0	0.3	0.32863	0.6	0.60386	0.9	0.79691	2.0		0.99532
0.1	0.11246	0.4	0.42839	0.7	0.67780	1.0	0.84270	2.5		0.99959
0.2	0.22270	0.5	0.52050	0.8	0.74210	1.5	0.96611