Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема1-6

1.6. Закон Дарси. Уравнение фильтрации жидкости в пористой среде.

1.6.1.Пористая среда и ее свойства.

Еще один большой класс задач тепломассопереноса - задачи о движении жид­костей и га­зов в пористой среде; такое движение часто называют фильт­ра­ци­ей. Теория фильтрации име­­ет большое значение в нефтегазодобыче, гидро­тех­нике, мелиорации и пр.

Пористая среда представляет собой твердое тело ("скелет"), пронизанное сис­темой со­об­щающихся между собой пустот (пор), имеющих нерегулярный ха­рактер и делающих среду про­ницаемой для жидкостей и газов. Характерные раз­меры пор - единицы или десятки мик­ро­мет­ров. Скелет пористой среды обыч­но состоит из зерен пес­ча­ни­ка или известняка различной фор­мы и раз­ме­ров, расположенных случайно и связанных меж­ду собой каким-либо це­мен­ти­ру­ющим материалом.

Первая важнейшая характеристика пористой среды - ее пористость m. Это отношение объема пор V_п к общему объему образца V:

m = V_п /V. (1.6.1)

Пористость - безразмерная величина; обычно ее указывают в процентах. Мож­но уточ­нить понятие пористости: различать полную пористость, когда учи­тываются все поры, и ак­тив­ную пористость, когда учитываются лишь те по­ры, которые входят в единую систему со­е­ди­ненных между собой пор и могут быть заполнены жидкостью извне. В теории фильтрации су­щественна лишь ак­тив­ная по­ристость, поэтому именно она в дальнейшем будет пониматься под по­ристостью. Ха­рак­тер­ные значения пористости некоторых природных ма­те­риа­лов при­ве­де­ны в таблице 1.2.

1.6.2.Закон Дарси.

Основной характеристикой фильтрационного движения является ско­рость фильт­ра­ции:

, (1.6.2)

где dM - масса жидкости, протекающая за единицу времени через площадку dS в направлении нор­мали к этой площадке,  - плотность жидкости. Уточним, что в этом определении под dS по­нимается полная площадь, а не только та ее часть, ко­торая занята порами. Фильтрационное дви­жение является обычно очень мед­лен­ным. Например, при разработке нефтяных место­рож­де­ний характерная ско­рость фильтрации в основной части пласта  0.005 см/с и меньше.

Фильтрационное движение жидкости или газа в пористой среде про­ис­хо­дит под дей­ст­ви­ем перепада давления. Связь между скоростью фильтрации и по­лем давления p, вы­зы­ва­ю­щим фильтрационное движение, впервые была ус­та­нов­лена экспериментально в 1856 году фран­цузским инженером Дарси (Darcy). Эта зависимость называется законом Дарси и имеет вид:

, (1.6.3)

где  - вязкость жидкости, а величина k называется проницаемостью пористой среды и яв­ля­ет­ся второй ее важнейшей характеристикой. Проницаемость имеет размерность площади и из­ме­ря­ется в единицах, называемых дарси (Д): 1Д = 1.0210^-8см² = 1.0210^-12м². Характерные зна­че­ния проницаемости некоторых при­родных материалов при­ве­дены в таблице 1.3. Обратим вни­мание на то, что по своей фор­ме закон Дарси ана­ло­ги­чен законам Фурье и Фика.

1.10.3.Уравнение непрерывности для пористой среды.

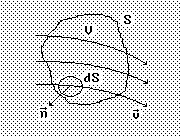
Выделим (мы­с­лен­но) в пористой среде объ­ем V, огра­ни­чен­ный зам­к­ну­той по­­верх­ностью S (см. ри­су­нок). Внутри этого объема на­ходится количество жид­кости, равное

. (1.6.4)

Вы­де­лим на по­верх­ности S ма­лый учас­ток dS с век­тором нор­ма­ли . Умножив (скалярно) век­тор ско­рос­ти на вектор нормали и на площадь dS, найдем объем жид­кости, протекающей за еди­ни­цу времени через участок dS. Умножив этот объем на плот­ность , найдем массу жид­кос­ти, про­текающей за единицу вре­ме­ни че­рез участок dS. Поэтому поток жидкости через всю по­верх­ность S за единицу времени равен интегралу

, (1.6.5)

а закон сохранения массы можно записать в виде:

, (1.6.6)

где знак минус в правой части соответствует физическому смыслу: по­ло­жи­тель­ный поток че­рез поверхность S означает уменьшение количества жидкости, на­ходящейся внутри объема V, и наоборот. Преобразуя интеграл по по­верх­нос­ти в интеграл по объему (по теореме Ост­ро­град­ского-Гаусса, аналогично тому, как это было сделано при выводе уравнений теп­ло­про­вод­нос­ти и диффузии), находим:

, (1.6.7)

или в дифференциальной форме:

. (1.6.8)

Это и есть уравнение непрерывности для пористой среды. От уравнения не­прерывности для сплошной среды, известного из курса гидродинамики, оно от­личается наличием мно­жи­те­ля m (пористости). Если устремить m  1 ("ске­лет" исчезает, остается только жидкость), то урав­нение (1.6.8), как и должно быть, переходит в обычное уравнение непрерывности для сплошной сре­ды.

1.6.4.Уравнение фильтрации (уравнение пьезопроводности).

В первом приближении зависимостью пористости и проницаемости по­рис­той среды, а также зависимостью вязкости жидкости от давления можно пре­небречь. Зависимостью же плот­ности жид­кости от давления (при тех дав­ле­ни­ях, которые характерны для подземной ги­д­ро­ди­на­ми­ки) пренебрегать часто уже нельзя, по­этому будем считать, что m = const, k = const,  = const, а плот­ность фильтрующейся жидкости есть функ­ция дав­ле­ния:  = (p). Обозначим че­рез _p ко­эф­фициент сжимаемости жидкости:

,

тогда

. (1.6.9)

Запишем уравнение непрерывности (1.6.8) в виде:

и подставим сюда закон Дарси (1.6.3) и формулы (1.6.9):

. (1.6.10)

Обычно градиенты давления сравнительно невелики, поэтому квадратом градиента дав­ле­ния можно пренебречь, и уравнение (1.6.10) принимает вид:

, (1.6.11)

где коэффициент  = k/(m_p) называется коэффициентом пьезопроводности; он имеет такую же размерность, как и коэффиценты температуропроводности и диф­фузии: м²/с. Уравнение (1.6.11) называется уравнением фильтрации, или урав­нением пьзопроводности; по своей фор­ме оно аналогично уравнениям теп­ло­проводности и диффузии; это означает, что методы ре­ше­ния этих уравнений од­ни и те же. В результате решения уравнения пьезопроводности оп­ре­де­ля­ет­ся по­ле давлений, аналогично тому, что в результате решения уравнения теп­ло­про­­вод­нос­ти определяется поле температур. После того, как определено поле дав­лений, по закону Дарси можно определить поле скоростей.

1.6.5.Заключительные замечания.

Изложенные выше элементы теории фильтрации хорошо описывают про­с­тейший слу­чай: изотермическую однофазную фильтрацию, т.е. движение од­но­фазной жидкости при по­сто­янной температуре, на­при­мер, воды, некоторых ви­дов чистой нефти, керосина (керосин часто ис­поль­зу­ется в лабораторных ис­сле­дованиях образцов пористых сред). Если температура в процессе фильт­ра­ции заметно меняется, то вязкость жидкости (ко­то­рая, как правило, сильно за­ви­сит от температуры) нельзя считать постоянной величиной и вы­носить из-под знака производных. Уравнение фильтрации в этом случае, во-первых, ста­но­­вит­ся слож­нее, а во-вторых, его приходится решать совместно с уравнением теп­ло­про­вод­нос­ти; обычно это удается сде­лать только численными методами.

Еще более сложной является многофазная фильтрация, т.е. одно­вре­мен­ное движение двух или нескольких жидкостей в пористой среде, например, дви­­жение водонефтяной или га­зо­водонефтяной смеси. Как показывает опыт, коэф­фициент проницаемости для разных фаз (для воды, нефти, газа) различен, и к тому же зависит от соотношения объема фаз в породе, т.е. меняется со вре­ме­нем. Поэтому приходится различать абсолютную и фазовую про­ни­ца­е­мос­ти. Та проницаемость, которая фигурирует в формуле (1.6.3) - это абсолютная про­ни­ца­е­мость, которая определяется при фильтрации единственной фазы, хи­ми­чес­ки инертной к по­ро­де; в лабораториях обычно для этой цели используется га­зообразный азот или воздух. При наличии в поровом пространстве более од­ной фильтрующейся фазы закон Дарси и уравнение фильт­рации резко ус­лож­ня­ют­ся, но именно этот случай характерен для нефтегазодобычи и по­э­тому наи­бо­лее интересен с практической точки зрения. Многофазная фильтрация - это те­ма от­дельного спецкурса.