Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема3-5

3.5.Температурное поле линейного непрерывного источника в неограни­чен­ной среде. Интегральная показательная функция.

Требуется определить температуру неограниченной сре­ды, нагреваемой линейным источником тепла мощ­но­стью W на единицу длины. Например, это может быть сква­жина или трубопровод на достаточно большой глу­би­не. Будем искать решение задачи с помощью фун­да­мен­тального решения уравнения теплопроводности. Пред­ставим ось z ис­точ­ником тепла, имеющим (формально) бесконечную длину. В действительности длина трубы и расстояние до границ области должны быть много больше, чем расстояние до точки наблюдения, а радиус трубы должен быть много меньше этого расстояния.

Найдем сначала температурное поле мгновенного линейного источника. Пусть на отрезке dz оси z в момент времени t мгновенно выделилось ко­ли­че­с­т­во тепла, равное qdz. Тогда, учитывая, что x = y = 0, r² = x² + y², по­лу­ча­ем:

(3.5.1)

Эта формула определяет температурное поле мгновенного линейного источ­ника тепла. Теперь для нахождения решения задачи проинтегрируем по­лу­чен­ный результат по t от 0 до t, полагая dq = Wdt и учитывая, что ca = :

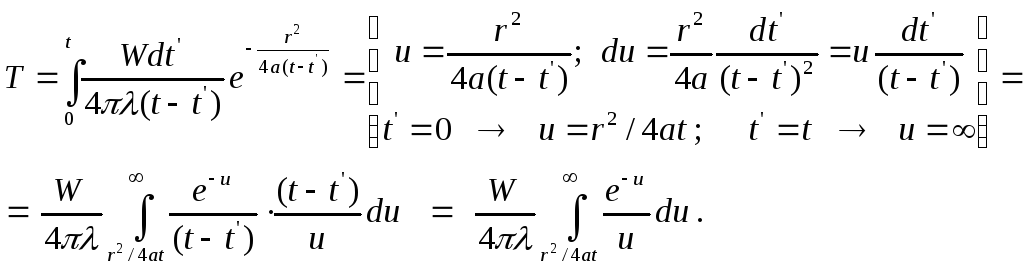(3.5.2)

Интеграл

(3.5.3)

ч

Рис. 3.5.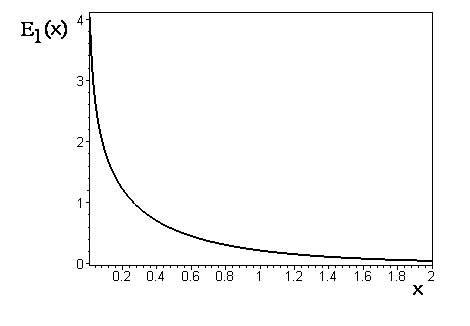

ерез элементарные функции не вы­ра­жа­ет­ся и назы­вается экспоненциальным интег­ра­лом, или интегральной по­ка­за­тель­ной функцией. По некоторым причинам, свя­зан­ным с историей изучения этой фун­к­ции, ее иногда обозначают как -Ei(-x), но для наших задач такое обозначение менее удоб­но, и мы не будем им пользоваться. Это вторая специальная фун­кция (после знакомой уже нам фун­к­ции erf(x)), ко­торая играет важную роль в теплофизике. Ее свойства, так же, как и свой­ства erf(x), хорошо изучены, функция табулирована, имеются графики и про­грам­мы для ее вычисления. График функции E₁(x) изображен на рис. 3.5, а не­ко­то­рые ее значения приведены в таблице 3.2. Разложение этой функции в ряд име­ет вид:

, (3.5.4)

где - постоянная Эйлера. Для малых x (т.е. для x << 1) можно в формуле (3.5.4) отбросить сумму , тогда

. (3.5.5)

Итак, температурное поле непрерывного линейного источника в неогра­ниченной среде выражается формулой:

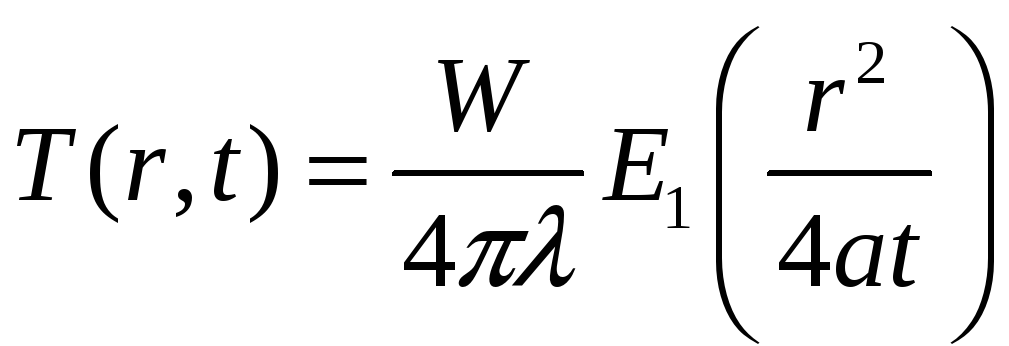, (3.5.6)

это точная формула. Для больших значений времени t можно вос­поль­зо­вать­ся приближенной формулой (3.5.5), т.к. большие t соответствуют малым зна­че­ни­ям аргумента. Поэтому при больших t:

. (3.5.7)

С ростом t температура в любой точке среды неограниченно растет, но мед­ленно (логарифмически).

Таблица 3.2. Некоторые значения функции E₁(x).

x	E1(x)	x	E1(x)	x	E1(x)	x	E1(x)	x	E1(x)
0.0		0.10	1.823	0.50	0.5598	1.1	0.1860	1.8	0.06471
0.01	4.038	0.15	1.464	0.60	0.4544	1.2	0.1584	2.0	0.04890
0.02	3.355	0.20	1.223	0.70	0.3738	1.3	0.1355	2.2	0.03719
0.03	2.959	0.25	1.044	0.80	0.3106	1.4	0.1162	2.5	0.02491
0.04	2.681	0.30	0.9057	0.90	0.2602	1.5	0.1000	3.0	0.01305
0.05	2.468	0.35	0.7942	1.00	0.2194	1.6	0.08631	5.0	0.001148