12.3 Уравнение баланса внутренней энергии многофазной среды в контрольных объемах.

Уравнение баланса внутренней энергии ((12.2)п.12.1) многофазной среды состоящей из газовой фазы (водяной пар и воздух), жидкой фазы (свободная и связанная воды) и твердой фазы (лед, сухой пористый материал) запишем в приближении однотемпературной среды и пренебрежения мощностью внутренних сил:

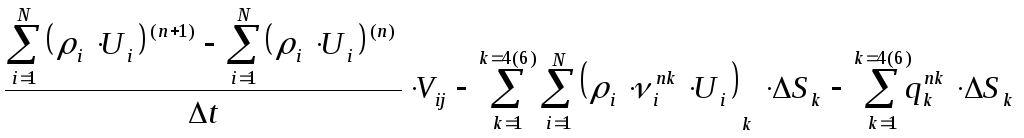, (12.12)

где верхние индексы (n) и (n+1) соответствуют моментам времени t⁽ⁿ⁾ и t⁽ⁿ⁺¹⁾=t⁽ⁿ⁾+Δt, индексы k=1,2,3,4 соответствует четырем граням контрольных объемов при 2D – моделировании, k=1,2,…,6 – шести граням КО при 3D – моделировании; N=5 – число фаз (компонент), причем индексы i=1,2,3,4,5 относятся соответственно к параметрам паров воды (i=1), воздух (i=2), влаги (i=3), льда (i=4), сухого материала (i=5), U_i, Дж/кг – удельная внутренняя энергия компонентов, q_k^nk, Вт/м² – удельный тепловой поток через к-ю грань ΔS_k контрольного объем V.

Внутренняя энергия фаз в многофазной среде является аддитивной функцией. Тогда для моментов времени t⁽ⁿ⁾ и t⁽ⁿ⁺¹⁾ получим для внутренней энергии ρU смеси в целом для контрольного объема V_ij:

(12.13)

(12.14)

Удельная внутренняя энергия сред, не испытывающих фазовых переходов, определяется с точностью до постоянных. В средах с температурами фаз T=T(t,x,y,z): для воздуха - , для сухого материала -, где С_vв, С_см, Дж/кгК – удельная изохорная теплоемкость воздуха и удельная теплоемкость сухого материала. Для льда , где С_S – удельная теплоемкость льда, U_So, Дж/кг – несущественная константа, которая принимается равной нулю. Для воды , для водяного пара, гдеC_l, C_vп – удельные теплоемкости воды и пара, а константы U_lo и U_So являются существенными константами при наличии фазовых переходов типа вода-пар l↔п и вода-лед l↔S. Эти константы определяются условиями нормировки при фазовых переходах

, (12.15)

, (12.16)

где i_S, i_l, i_п, Дж/кг – удельные энтальпии льда, воды и водяного пара при условиях фазовых переходов; l_Sl, l_lп, Дж/кг – удельная теплота фазовых переходов лед-вода и вода-пар.

Для льда и полагаяT_So=0, T=T_So, U_So=0. Тогда удельная внутренняя энергия льда

(12.17)

и удельная энтальпия равна .

Удельная внутренняя энергия воды записывают в виде

, (12.18)

а удельная энтальпия воды в виде

. (12.19)

Тогда, по условию нормировки при плавлении льда, получаем

, откуда начальное значение удельной внутренней энергии воды

, (12.20)

и расчетная формула для удельной внутренней энергии воды имеет вид

,

где существенная константа U_lo определяется формулой (12.20). Константу U_по находим по условию нормировки при испарении воды, с учетом удельной теплоты испарения воды l_lп:

. (12.21)

Удельная энтальпия воды с учетом формулы (2.19) и (2.20) записывается как

.

Водяной пар при условиях по температурам и давлениям, характерных для ограждающих конструкций зданий может считаться идеальным газом. Тогда удельная внутренняя энергия пара запишется в виде

, (12.23)

Удельная энтальпия пара равна

.

Из условия нормировки (2.22) получаем

.

Следовательно

, (12.24)

где U_lo определено выражением (12.20), а U_п выражением (12.23).

Полная энергия смеси (12.13), (12.14) с одинаковой температурой компонент запишется в виде

обозначим и.

Из (2.12) получим для КО V_ij:

(12.25)

где - тепловая мощность, подводимая к контрольному объемуV_ij через его грани механизмом теплопроводности (рис.12.2).

Температуры на гранях W, E, S, N определяем из условий равенства тепловых потоков через грани. Так, например, для грани W имеем

, (12.26)

откуда

(12.27)

Аналогично выражаем температуры на гранях E, S, N

(12.28)

Рис.12.2 К определению тепловой мощности и потоков массы фаз подводимой через грани W,E,S,Nк контрольному объемуV_ij(2D).

Тепловая мощность Q, Вт подводимая через грани W, E, S, N к контрольному объему V_ij выражается с учетом (12.27)-(12.28)

(12.29)

Тогда тепловая мощность, подводимая к контрольному объему V_ij равна

. (12.30)

Разделив (12.25) на (ρС)ⁿ⁺¹ получим

, (12.31)

где ;

- изменение температуры, связанное с изменением по времени приведенных плотностей пара и воды и ненулевыми значениями констант U_по и U_lо;

- изменение температуры из-за потока внутренней энергии пара через грани КО;

- изменение температуры из-за потока внутренней энергии воздуха через КО;

- изменение температуры из-за потока внутренней энергии влаги через КО;

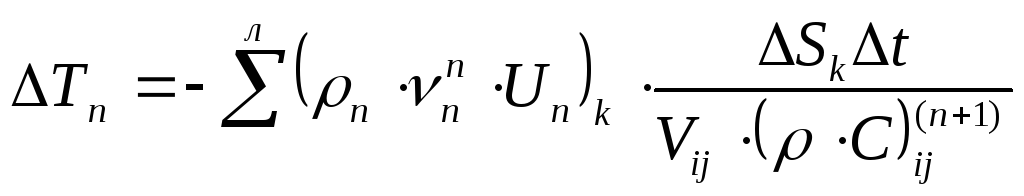- изменение температуры из-за потока тепла через грани КО вследствие теплопроводности.

Приведение уравнения баланса внутренней энергии к виду (12.31) позволяет оценивать влияние и относительную значимость отдельных физических механизмов теплопереноса по приращениям температуры ΔТ_о, ΔТ_п, ΔТ_в, ΔT_l, ΔT_q.