Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема2-4

2.4.Задача о притоке жидкости к скважине (стационарная одномерная осе­сим­метричная задача фильтрации).

Рассмотрим пористую среду, насыщенную неф­тью, водой или газом. Часто такая среда представляет собой достаточно про­тя­женный в горизонтальном на­прав­лении пласт, огра­ни­чен­ный сверху и снизу не­про­ни­ца­е­мы­ми поверхностями (их называют кровлей и по­дошвой). Размеры пласта в горизонтальном на­прав­ле­нии измеряются километрами, а типичное значение толщины h - не­сколько мет­ров. Будем считать, что пласт полностью насыщен жид­костью, и дав­ление во всех его точках (оно называется вну­три­­плас­то­вым давлением) выше ат­мо­с­фер­но­го. Поэтому если в пла­сте пробурена скважина (радиуса b, как показано на ри­сунке), то под действием градиента дав­ления к скважине начинает двигаться жид­кость, насыщающая пласт. Говоря формально, дви­жение жидкости нач­нет­ся во всем пласте, однако для любой скважины можно более или ме­нее точно ука­зать радиус области вокруг скважины, за пределами которой скорость филь­т­­ра­ции будет пре­не­брежимо мала (на рисунке эта область ограничена ци­лин­д­ри­ческой по­верх­ностью радиуса R). Типичное значение радиуса скважины b - не­сколько сантиметров, а радиус области фильтрации R  100 м. В процессе экс­­плу­а­та­ции скважины обычно существует до­воль­но дли­тель­ный период вре­ме­ни, когда скважина ра­бо­тает в стационарном ре­жиме, при ко­то­ром давление и скорость дви­же­ния жид­кости в пласте вокруг скважины, а так­же количество до­бы­ваемой за единицу времени жид­кос­ти (дебит скважины) со временем поч­ти не меняется. Найдем решение задачи фильтрации для этого случая.

Уравнение пьзопроводности (фильтрации) (1.6.11) в стационарном ре­жи­ме (p/t = 0) в цилиндрической системе координат принимает вид:

. (2.4.1)

Это уравнение полностью аналогично стационарному уравнению тепло­про­вод­нос­ти в ци­линд­ри­ческих координатах (2.2.1), поэтому его интегрирование дает ре­зультат, аналогичный фор­му­лам (2.2.2) и (2.2.3):

; (2.4.2)

, (2.4.3)

где C₁ и C₂ - константы интегрирования, которые должны быть определены из граничных ус­ло­вий. Граничные ус­ловия задаются на стенках скважины (ус­ло­вие заданного по­сто­ян­ного дав­ления либо условие заданного постоянного рас­хо­да), а также на внешней границе области фильтрации, которая на­зы­ва­ет­ся кон­туром питания.

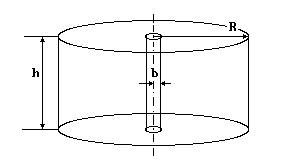
Пусть контур питания имеет радиус R, а давление на нем равно p_о (ве­ли­чи­на p_о на­зы­ва­ет­ся начальным внутрипластовым давлением):

p_{r = R} = p₀ , (2.4.4)

это первое граничное условие.

Далее, пусть на поверхности скважины задан постоянный поток жидкости (дебит) Q, ко­то­рый, очевидно, ра­вен произведению "рабочей" площади по­верх­нос­ти скважины 2bh на ско­рость движения жид­кости на поверхности сква­жи­ны:

-2bhv_r=b = Q. (2.4.5)

Формула (2.4.5) пригодна как для добывающей, так и для нагнетательной сква­жи­ны, знак "ми­нус" в ней учитывает направление скорости фильтрации. Если сква­жина является до­бы­ва­ю­щей, ее дебит считается положительным, а ско­рость жидкости направлена к оси скважины, т.е. отрицательна. Для на­гне­та­тель­ной скважины, наоборот, дебит отрицателен (жидкость за­ка­чи­ва­ют в пласт), а скорость на­прав­ле­на из скважины в пласт, т.е. положительна.

Согласно закону Дарси (1.6.3), скорость фильтрационного движения жид­кос­ти оп­ре­де­ля­ет­ся градиентом давления. На поверхности скважины эта ско­рость равна:

.

Подставляя это равенство в (2.4.5), получаем второе граничное условие:

. (2.4.6)

Подставляя (2.4.6) в (2.4.2), определяем константу С₁, а затем из условия (2.4.4) и общего решения (2.4.3) находим константу С₂ :

, .

Таким образом, давление в пласте в области b  r  R определяется формулой:

; (2.4.7)

в частности, давление на поверхности скважины (его иногда называют дав­ле­ни­ем на забое, или забойным давлением) равно

. (2.4.8)

Скорость фильтрации в пласте, согласно закону Дарси, определяется формулой

. (2.4.9)

Формулы (2.4.7) - (2.4.9) иногда называют формулами Дюпюи (Dupuit); они справедливы как для добывающих, так и для нагнетательных скважин, ра­бо­тающих в стационарном ре­жи­ме. На приведенных ниже рисунках изображен примерный вид профиля давления и аб­со­лют­ной величины ско­рос­ти филь­тра­ции в том и другом случае. Для до­бы­ва­ю­щей скважины Q > 0, b < R, поэтому по фор­муле (2.4.8) дав­ление на поверхности скважины p_b  получается меньше вну­три­плас­то­во­го дав­ления, как и дол­жно быть. Для нагнетательной сква­жины Q < 0, поэтому по формуле (2.4.8) по­лучаем p_b > p₀, т.е. для того, чтобы за­ка­чать жидкость в пласт, надо с по­мо­щью насосов соз­дать такое дав­ле­ние на за­бое, которое пре­вы­шает внутрипластовое дав­ле­ние.

Примерный вид кривых давления и модуля скорости фильтрации вокруг добывающей (слева) и нагнетательной (справа) скважин.