Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема4-1

4. ЗАДАЧИ С ФАЗОВЫМИ ПЕРЕХОДАМИ (ЗАДАЧИ СТЕФАНА).

Многие процессы тепломассопереноса связаны с изменением агрегатного со­стояния ве­щест­ва (это задачи о промерзании и протаивании влажного грунта, об образовании льда на по­верх­ности воды, о промерзании трубопроводов, о пла­в­лении и затвердевании металла и др.). Ре­шение подобных задач имеет боль­шое практическое значение в строительстве, особенно в рай­онах вечной мер­з­лоты, в нефтегазодобыче, в металлургии и в других прикладных дис­цип­ли­нах. Изменение физического со­сто­я­ния вещества происходит при изменении тем­­пе­ра­туры те­ла, в частности, при охлаждении ниже точки плавления про­ис­хо­дит переход из жид­кой фазы в твер­дую. При этом в первом приближении мож­но считать, что на поверхности фа­зо­вого пе­ре­хода все время сохраняется по­стоянная тем­пе­ра­ту­ра и происходит выделение скры­той теп­ло­ты затвер­де­ва­ния.

4.1.Задача о промерзании влажного грунта (классическая задача Сте­фа­на).

Классическим примером яв­ля­ет­ся задача о промерзании влажного грунта, которую ре­шил в середине 19-го века вен­с­кий ма­те­матик Стефан (Stefan); с тех пор подобные задачи но­сят имя задач Стефана.

Постановка задачи. Влажный грунт находится в талом состоянии и име­ет всюду на­чаль­ную температуру T_н, которая выше температуры замерзания (тем­пературы фазового пе­ре­хо­да) T_ф. В момент времени t = 0 на поверхности грун­та x = 0 скачком уста­нав­ли­ва­ет­ся, а за­тем поддерживается температура T₀, ко­торая ниже температуры замерзания T_ф. В результате это­го у поверхности грун­та появляется промерзший слой, толщина которого со временем уве­ли­чи­ва­ется. Требуется найти закон движения фронта промерзания и распределение тем­пе­ра­ту­ры в промерзшей и талой зонах.

Классическое решение. Обозначим через x₁ ко­ор­динату фрон­та промерзания, через T₁(x,t) тем­пе­ра­ту­ру в промерзшем слое 0  x  x₁, а через T₂(x,t) - тем­пе­ра­туру в еще не про­мер­з­шей (та­лой) области x₁  x <  (см. рисунок). Тогда задача о про­мер­за­нии грунта мо­жет быть сформулирована как задача о со­пря­же­нии двух температурных по­лей на движущемся фронте про­мер­за­ния, т.е. сведена к решению урав­не­ний теп­лопроводности

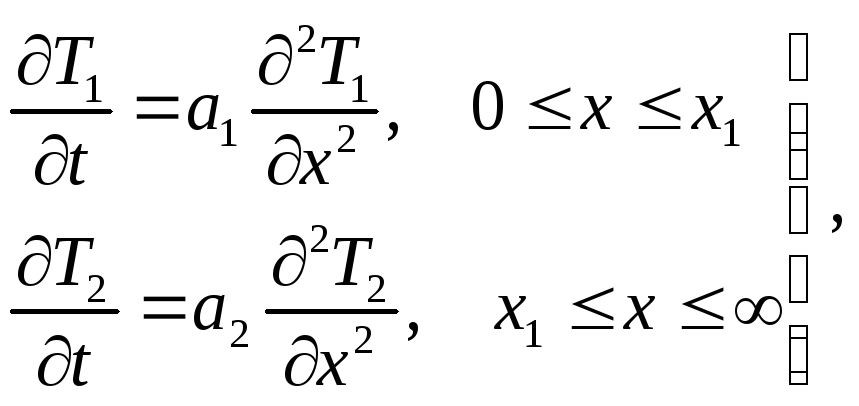(4.1.1)

где a₁ и a₂ - коэффициенты температуропроводности в мерзлой и талой зонах соответственно, с начальным условием

T₂(x,0) = T_н , (4.1.2)

с граничным условием на неподвижной границе (поверхности) х = 0:

T₁(0,t) = T₀ < T_ф, (4.1.3)

и условиями на фронте промерзания:

. (4.1.4)

В дальнейшем положим для краткости записи T_ф = 0; это всегда можно сделать, выбрав нуж­ное начало от­счета температурной шкалы (для задач о промерзании или протаивании во­ды это просто оз­на­чает переход на шкалу Цельсия).

Т.к. фронт движется с неизвестной заранее скоростью, то на нем, кроме гра­ничных ус­ло­вий (4.1.4) для уравнений теплопроводности, должно быть за­да­но еще одно условие, оп­ре­де­ля­ю­щее скорость движения фронта. Пусть за время dt фронт смещается на расстояние dx₁; при этом замерзает масса воды, равная Sdx₁ и выделяется количество тепла LSdx₁, где S - пло­щадь фронтовой по­верх­ности, L - удельная теплота фазового перехода,  - масса воды в еди­ни­це объ­ема грунта. По закону сохранения энергии это количество тепла должно рав­няться раз­нос­ти количеств тепла, прошедших через фронт со стороны талой и мерзлой зон:

,

или

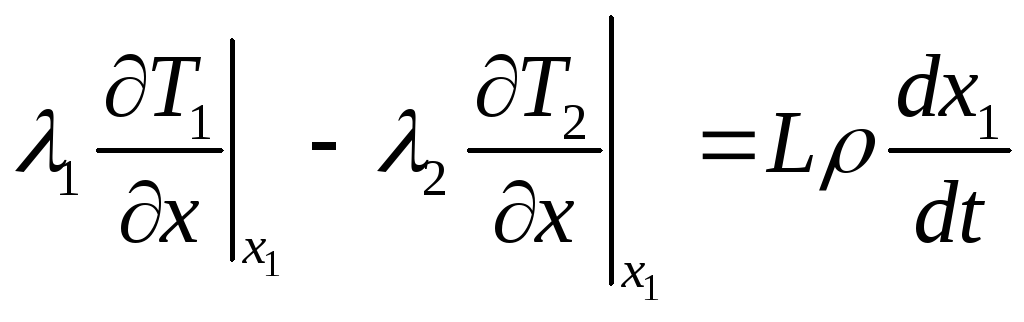. (4.1.5)

Это условие иногда называют условием Стефана на фронте фазового перехода.

Выше мы видели, что одномерное температурное поле в полу­огра­ни­чен­ной сре­де выражается через интеграл вероятностей erf, поэтому будем искать решение уравнений (4.1.1) в виде:

, ,

где A₁, A₂, B₁, B₂ - неизвестные пока константы, которые должны быть определены из на­чаль­но­го и граничных условий. Из условия (4.1.3) находим:

A₁ = T₀, (4.1.6)

условие (4.1.2) дает:

A₂ + B₂ = T_н, (4.1.7)

а из условий (4.1.4) получаем:

= T_ф = 0. (4.1.8)

Для того, чтобы некоторая функция равнялась константе, необходимо, чтобы ее аргумент рав­нял­ся константе, поэтому равенства (4.1.8) возможны лишь в том случае, если

,

или

. (4.1.9)

Формула (4.1.9) дает ответ на вопрос о том, по какому закону движется фронт промерзания: его координата пропорциональна квадратному корню от времени промерзания, а коэффициент про­порциональности  - некоторая неизвестная пока константа, которая должна быть найдена в ходе дальнейшего решения.

Равенства (4.1.8) теперь можно записать в виде:

,

откуда

, (4.1.10)

и

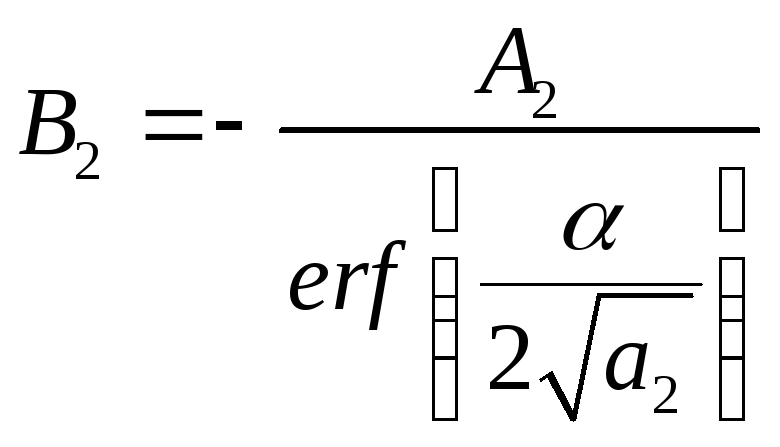. (4.1.11)

Решая совместно (4.1.7) и (4.1.11), находим:

, (4.1.12)

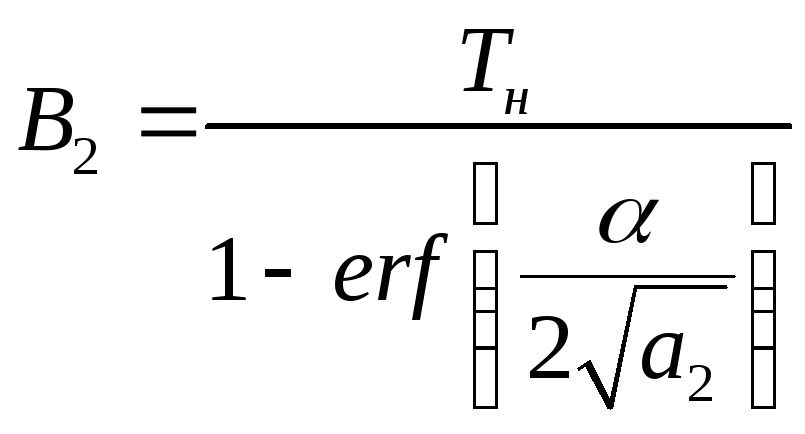. (4.1.13)

Итак, константы A₁, A₂, B₁, B₂ найдены (формулы (4.1.6), (4.1.10), (4.1.12), (4.1.13)), точ­нее, вы­ра­жены через неизвестную пока константу . Для опре­де­ле­ния константы  ис­поль­зу­ем условие Стефана (4.1.5), для чего запишем сначала формулы для и :

,

.

Полагаем x = и подставляем эти формулы в (4.1.5):

.

Сокращая на , получаем трансцендентное уравнение относительно :

. (4.1.14)

Это уравнение имеет решение при T₀ < 0 и T_н  0, т.к. в этом случае при из­ме­не­нии  от 0 до  ле­вая часть меняется от - до +, а правая часть - от 0 до -. В “до­компьютерные” времена ре­шение подобных уравнений обычно находили гра­фически: чертили зависимость левой части от , за­тем на этом же графике чер­тили зависимость правой части от , и точка пересечения давала ре­шение. В на­стоящее время имеется несколько эффективных алгоритмов численного ре­ше­ния подобных урав­нений с помощью компьютера, и разработано большое ко­личество стандартных программ на различных языках программирования. Эти алгоритмы (например, ме­тод “вилки”, или по­ло­вин­ного деления, метод ка­са­тельных, метод хорд и др.) подробно опи­са­ны в курсах численных методов анализа, поэтому останавливаться на них здесь нет не­об­хо­ди­мости.

Таким образом, если заданы теплофизические параметры вещества ₁, ₂, a₁, a₂, L, , а так­же граничная и начальная температуры T₀ < 0 и T_н  0, то кон­с­тан­та , а вслед за ней и кон­станты A₁, A₂, B₁, B₂ определяются однозначно.

Упрощенные решения. Если начальная температура равна температуре фа­зового пе­ре­хо­да: T_н = T_ф = 0, то урав­не­ние (4.1.14) упрощается. Физически это означает, что талая зона пред­ставляет собой жид­кость, в которой благодаря хо­рошей конвекции имеет место по­сто­ян­ст­во температуры (за­да­ча об об­ра­зо­ва­нии льда на поверхности воды). Обозначив:

,

запишем это уравнение в виде:

,

или

, (4.1.15)

где

< 0, т.к. T₀ < 0.

Левая часть уравнения (4.1.15) - это универсальная (пригодная для задачи с лю­бы­ми па­ра­мет­ра­ми) функция , график которой легко построить, а правая часть - прямая линия, проходящая че­рез начало координат под уг­лом, определяемым ко­эффициентом D, поэтому данное урав­не­ние легко решается как графически, так и численно. Если  << 1, т.е. если  << , то фун­к­ции и erf() в урав­не­нии (4.1.15) можно разложить в ряд, ограничившись первыми чле­на­ми раз­ло­же­ния:

, .

Тогда из уравнения (4.1.15) получаем:

, отсюда . (4.1.16)

Знак “минус” под корнем напоминает, что полученная формула, как и все ре­ше­ние, имеет смысл только если T₀ < 0.

Аналогичным образом может быть решена задача о протаивании за­мер­з­ше­го грунта.