Кислицын Шабаров УМК Тепломассообмен / КраткийКонспектЛекций / Тема3-4

3.4.Нестационарное одномерное температурное поле в неограниченной и полуограниченной сре­де.

Температурное поле мгновенного плоского источника. Пусть в каж­дой точке (точнее, на каждом участке с размерами dy'dz') некоторой плос­кос­ти x' = const в момент времени t' мгновенно вы­де­­лилось количество тепла, равное qdy'dz'. Пред­ста­вим эту плоскость источником тепла, име­ю­щим бес­ко­неч­ные размеры в y- и z-на­прав­ле­ниях, и проинтегрируем фундаментальное решение (3.11) по y' и z' от - до +:

=

=.

Сделаем в интеграле по z' замену переменных: (z-z')²/[4a(t-t')] = ². Тогда , и интеграл преобразуется в интеграл Пуассона, умноженный на . Совершенно ана­ло­­гично преобразуется интеграл по y'. Таким образом, интегри­ро­вание по y' и z' дает мно­жи­тель 4a(t-t'), и в результате получаем:

. (3.4.1)

Формула (3.4.1) определяет одномерное температурное поле, создаваемое мгно­венным плос­ким источником тепла в неограниченной среде, т.е. температуру точки среды с координатой x в любой момент вре­мени t > t', если в плоскости с ко­ординатой x' момент времени t' мгновенно выделилось количество тепла, рав­ное q (на еди­ни­цу площади).

Температурное поле непрерывного плоского источника. Пусть в плос­кости x' = const в момент времени t' = 0 начинает непрерывно действовать плос­кий источник тепла с мощностью W на единицу площади. Выберем для крат­кос­ти записи x' = 0, т.е. поместим начало координат в плоскость, где находится ис­точник. За время dt' этот источник выделяет количество тепла, равное q = Wdt' (на единицу площади). Для нахождения температурного поля, соз­да­вае­мо­го этим источником, проинтегрируем формулу (3.4.1) по t' от 0 до t:

. (3.4.2)

Сделаем замену переменных: x²/[4a(t - t')] = ². Тогда: (t - t')^1/2 = x/(2a^1/2), dt' = x²d/(2a³), пределы интегрирования: t' = 0  , t' = t   = , и фор­мула принимает вид:

.

Учтем, что ca = . Интегрируем по частям. Обозначим: . Тогда , и получаем:

.

Первый интеграл в скобках справа - это интеграл Пуассона. Раскрывая скобки и сравнивая по­лу­ченный результат с формулой (3.3.9), находим:

. (3.4.3)

Эта формула определяет температурное поле непрерывного плоского ис­точ­ни­ка в не­о­гра­ни­чен­ной среде.

Нагрев полу­ограни­чен­ной среды постоянным по­то­ком тепла. Рассмотрим теперь полуограниченную среду (это может быть большой участок грунта с ровной по­верх­ностью, стена большой тол­щи­ны, толстая пластина и т.п.), нагреваемую по­сто­ян­ным тепловым по­­то­ком с плот­ностью мощности W = const (см. ри­су­нок). Считая каж­дую точку нагреваемой по­верх­ности источ­ни­ком теп­ла, мы мо­жем применить полученный результат для оп­ре­де­ле­­ния тем­пе­ра­тур­но­го поля в этой среде. Надо лишь учесть, что, в от­ли­чие от не­о­гра­ни­ченной среды, теп­ло будет рас­про­стра­няться толь­ко в на­прав­ле­нии x > 0, поэтому "эффективность" нагрева бу­дет в два ра­за выше, чем ес­ли бы тепло распространялось в обе стороны, сле­до­вательно, фор­му­ла, оп­ре­де­ля­ющая тем­пе­ра­турное поле в полу­огра­ни­ченной среде, отличается от формулы (3.4.3) мно­жи­те­лем 2:

. (3.4.4)

Изменение температуры в неограниченной среде. Пусть в неограни­чен­ной среде задано начальное распределение температуры T = f(x). Для того, чтобы определить, как это распределение будет изменяться со временем, можно каж­дую точ­ку среды считать источником с количеством тепла, равным:

q = cTdx' = cf(x')dx'.

Тогда температуру в любой точке среды в любой момент времени можно за­пи­сать в виде ин­те­гра­ла от (3.4.1) по x', полагая в этой формуле t' = 0:

. (3.4.5)

Формула (3.4.5) дает решение поставленной задачи, если задан конкретный вид функции f(x).

Рис. 3.4.

Рассмотрим пример, имеющий важное практическое значение. Пусть два одинаковых тела прямоугольной формы на­греты до раз­лич­ных тем­пе­ратур. Примем за нуль начальную тем­пе­ратуру более холодного тела, а начальную тем­пе­ра­ту­ру более на­гре­того тела обо­зна­чим через T₁. Пусть в момент времени t' = 0 эти те­ла при­ве­де­ны в со­прикосновение (см. рисунок), так что получается одно не­рав­но­мер­но нагретое тело, и пусть размер этого тела до­ста­точно велик, так что мож­но применить формулу (3.4.5). То­гда на­чаль­ное распределение температуры (функция f(x')) бу­дет иметь вид "ступеньки": нуль при x' < 0 и T₁ при x' > 0 (ли­ния 1 на ри­сун­ке 3.4), и фор­му­ла (3.4.5) при­ни­ма­ет вид:

. (3.4.6)

Вычисление этого интеграла приводит к следующему результату:

, x > 0. (3.4.7)

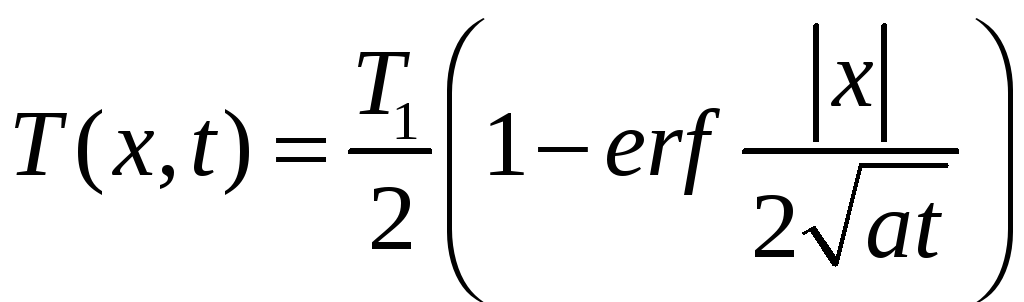, x < 0. (3.4.8)

На рис.3.4 изображен вид кривых T(x) в различные моменты времени t₁ и t₂ > t₁ (кри­вые 2 и 3). Тепло постепенно перетекает из более нагретой области в более хо­лодную. В пре­деле при t  , как видно из формул (3.4.7) и (3.4.8), во всей сре­­де установится одинаковая тем­пература T = T₁ /2 (линия 4), как и должно быть по закону сохранения энергии. В точке x = 0 (в плоскости со­при­кос­но­ве­ния тел) температура равна T₁ /2 в любой момент времени, как и долж­но быть из соображений симметрии.

Нестационарное одномерное температурное поле в полу­огра­ни­чен­ной сре­де с за­дан­ной постоянной температурой на поверхности. Если на­чаль­ная температура полуограниченной среды T₀ = const, а на ее поверхности x = 0, начиная с мо­мен­та времени t = 0 скачком устанавливается, а затем под­дер­жи­вается постоянная тем­пе­ра­ту­ра T₁, то вычисления, аналогичные про­ве­ден­ным выше, дают следую­щий результат:

. (3.4.9)

Если T₀ = 0, то

. (3.4.10)

Пример. Начальная температура толстой бетонной плиты (a = 4.210^‑7м²/с) равна T₀ = +10^оС. Поверхность этой плиты быстро нагрели до температуры T₁ = +100^оС (например, го­рячим паром), и поддерживают при этой температуре в течение нескольких часов. Какой ста­нет температура внутри плиты на глубине x = 10 см от поверхности через 5 ча­сов про­г­ре­ва?

Решение. Вычисляем аргумент = 0.575. По таблице в каком-либо справочнике находим erf(0.575) = 0.584. Подставляя в формулу (3.4.9), находим: искомая температура T = 47.4^оС.

Нестационарное одномерное температурное поле в полуограни­чен­ной сре­де с гранич­ным усло­вием третьего рода. Пусть начальная тем­пе­ра­ту­ра твердой полуограниченной среды T₀ = const. В мо­мент времени t = 0 ее по­верхность x = 0 начинает омывать жидкая или газообразная среда с по­стоянной температурой T_c. Теплообмен между этой средой и твердой поверхностью про­ис­­ходит по закону Ньютона (граничное условие третьего рода). Требуется найти рас­пре­де­ле­ние температуры по глубине в любой момент времени T(x,t), а также плотность теплового потока q(t), проходящего через поверхность.

Вычисления, аналогичные проведенным выше, но несколько более слож­ные, дают для температурного поля следующий результат:

, (3.4.11)

где H = / - относительный коэффициент теплообмена, а относительная без­раз­мерная тем­пе­ратура  связана с искомой температурой T(x,t) формулой:

. (3.4.12)

Формула (3.4.11) пригодна для расчета как нагрева, так и охлаждения тела. Если температура жидкости или газа T_c выше, чем начальная температура твердого тела T₀, то тело на­гре­вается. Тогда температура T(x,t) в любой точке в лю­бой момент времени меньше, чем T_c, поэтому чис­ли­тель и знаменатель в фор­муле (3.4.12) положительны, и относительная безразмерная тем­пе­ра­ту­ра  > 0. Если же температура жидкости или газа T_c ниже, чем начальная температура твер­дого тела T₀, то тело охлаждается. Тогда числитель и зна­ме­на­тель в фор­му­ле (3.4.12) отрицательны, но безразмерная тем­пе­ратура , как и в случае нагре­ва, положительна.

Если коэффициент теплообмена  очень велик (H  ), то второй член спра­ва в формуле (3.4.11) стремится к нулю, и решение, как и должно быть, сов­падает с формулой (3.4.10), т.к. граничное условие первого рода - это пре­дель­ный случай условия третьего рода при   ; при этом температура по­верх­­ности тела T₁ будет равна температуре окру­жа­ю­щей среды T_c.

На поверхности нагреваемого или охлаждаемого тела x = 0, и формула (3.4.11) упро­ща­ет­ся:

, (3.4.13)

где  ₁ - относительная безразмерная температура поверхности. Если H  , то  ₁  1, или T₁  T_c, как и должно быть.

Плотность теплового потока q через поверхность x = 0 можно определить с помощью закона Фурье:

.

Дифференцируя T(x,t) по x и приравнивая x нулю, находим:

. (3.4.14)

Как видно из полученной формулы, плотность теплового потока меняется со вре­ме­нем. При t = 0 она максимальна и равна (T_c - T₀). По мере прогрева из-за повышения тем­пературы поверхности эта величина постепенно умень­ша­ет­ся, и при t   плотность теп­ло­вого потока стремится к нулю.

Обратим внимание еще на одну особенность полученных формул. При боль­ших зна­че­ниях x и (или) t прямое использование формул (3.4.11), (3.4.13) и (3.4.14) становится не­у­доб­ным из-за резкого увеличения экспоненты и умень­ше­ния функции erfc. Попытка вычислить их произведение "в лоб" приводит к потере точности. В этом случае следует воспользоваться раз­ложением функции erfc(u) для больших значений аргумента u:

.

Например, формула (3.4.13) для больших значений времени t может быть записана в виде:

. (3.4.13')

Пример. Начальная температура толстой бетонной плиты ( = 0.92 Вт/мК, a = 4.210^-7м²/с) равна T₀ = +10^оС. Поверхность этой плиты на­чи­на­ют обдувать горячим воздухом с температурой T_с = +100^оС, и делают это в те­чение нескольких часов. Какой станет температура поверхности плиты и температура внутри плиты на глубине x = 10 см от поверхности через 5 ча­сов прогрева? Чему будет равна в этот момент плотность теплового потока через поверхность? Коэффициент теплообмена принять равным  = 4 Вт/м²К.

Решение. Сначала найдем относительный коэффициент тепло­обмена: H = / = 4.35 1/м. Далее най­дем температуру поверхности по формуле (3.4.11). Для это­­го вычисляем = 0.378. По какому-либо справочнику находим erfc(0.378) = 0.593. Далее находим показатель экс­по­нен­ты: H²at = 0.143. Под­ставляя в формулу (3.4.11), вычисляем:  ₁ = 0.316, откуда по формуле (3.4.12) находим искомую температуру поверхности: T₁ =  ₁(T_с - T₀) + T₀ = 38.4^оС. По формуле (3.4.14) находим плотность теплового потока: q = 243 Вт/м².

Теперь найдем температуру на глубине x = 10 см = 0.1 м. Вычисляем аргумент функции erfc в первом слагаемом формулы (3.4.11): = 0.575. По справочнику находим erfc(0.575) = 0.416. Подставляя в формулу (3.4.11), находим:  = 0.276. Отсюда по формуле (3.4.12): T =  (T_с - T₀) + T₀ = 34.9^оС.

Как температура поверхности, так и температура на глубине оказались меньше, чем в предыдущем примере, как и должно быть.

Пример. Рассмотрим аналогичную задачу на охлаждение. Пусть на­чаль­ная тем­пе­ра­тура плиты из предыдущего примера равна T₀ = +100^оС, тем­пе­ра­ту­ра холодного воздуха, ко­торым обдувают поверхность этой плиты равна T_с = +10^оС, а все остальные параметры те же самые. Тогда в формулах (3.4.11) и (3.4.12) ничего не меняется, и, значит, как и в пре­ды­ду­щем примере,  ₁ = 0.316, и  = 0.276. По формуле (3.4.12) находим искомую температуру по­верх­ности: T₁ =  ₁(T_с - T₀) + T₀ = 71.6^оС, и температуру на глубине: T = (T_с - T₀) + T₀ = 75.2^оС.