19 (2). Квантовые состояния многоэлектронных атомов. Правило Хунда.

Рассмотрим более сложные примеры.

Пусть один из электронов перешел в состояние l1 = 1, а второй может оказаться в состоянияхl2 = 0, 1, 2. Запишем возможные значенияLв виде таблицы:

Рассмотрим случайl2 = 1 (оба электрона в состоянииp). ТогдаL=0,1,2.

Если S= 0, тоJ=L,и возможны состояния:

при ,при ,при .

ЕслиS= 1, то количество термов будет больше, т.к. тогдаJ=L+1,L,L-1. ЕслиL=0, то .

Если L= 1, то возможно ЕслиL= 2, то возможно

Итак, двум p-электронам отвечает десять возможных состояний атома. Однако все они могут осуществиться только в том случае, если не нарушен принцип Паули. Еслиn1 иn2 (главные квантовые числа) различны, то могут осуществиться все десять возможных состояний. Если жеn1 =n2, то некоторые из найденных термов оказываются запрещенными принципом Паули.

Действительно, при данныхLиSвозможные значения магнитных квантовых чиселMLиMSопределяются условиями:

Составим таблицу возможных значенийML для двух эквивалентныхp-электронов (n1 =n2). Т.к. электроны эквивалентны, то заштрихованные клетки не дают ничего нового, и их следует исключить из рассмотрения (неважно,m1=1,m2=0 илиm1=0,m2=1, если электроны неразличимы).

Оставшиеся значения MLможно разбить на две группы:

Эти значения осуществляются, если m1=m2, это возможно, еслиms1 ≠ms2, т.е. еслиS=0. Поэтому в системе синглетных состояний (S= 0,k= 1) остаются состояния 1S0 и 1D2 (исключено состояние 1P1).

Если ms1 =ms2, т.е. еслиS=1, то невозможны состояния сm1=m2, поэтому значенияMLна главной диагонали (подчеркнуты) следует отбросить. Тогда остается только один ряд значенийML:

Поэтому в системе триплетных состояний остаются состояния .Итак, в случае двух эквивалентных p-электронов возможно существование только пяти состояний (вместо десяти для электронов сn1¹n2).

Аналогичные рассуждения можно провести для любого количества электронов, причем векторная модель очень точно предсказывает особенности спектров сложных атомов. После того, как найдены возможные термы атомов, возникает вопрос, какой из этих термов основной. На этот вопрос дает ответ правило, эмпирически установленное в 1926г Фридрихом Хундом (HundF.)

Правило Хунда.

Среди термов, принадлежащих одной электронной конфигурации, самым глубоким яляется тот, который связан с наибольшим значениемS, а среди термов с равнымS– тот, который связан с наибольшимL. При этом для основного терма , если оболочка заполнена менее, чем наполовину, и в остальных случаях. Другими словами, электроны в атоме стремятся (когда это не противоречит принципу Паули) оставаться не спаренными, т.е. иметь параллельные спины (при этомSбудет наибольшим).

Правило Хунда является следствием взаимного отталкивания электронов. Действительно, энергия атома (с учетом взаимодействия между электронами) тем меньше, чем дальше друг от друга находятся электроны. Если электроны имеют одинаковые n,lиms(спины параллельны), то они должны иметь различныеm, т.е. волновые функции с различными пространственными распределениями (“двигаться по разным орбитам”, говоря на языке теории Бора), поэтому такие электроны отстоят в атоме дальше друг от друга (в среднем), чем спаренные (с антипараллельными спинами); следовательно, в таком состоянии атом обладает меньшей энергией, т.е. терм находится ниже.

В качестве примера рассмотрим атом, который имеет два валентных p– электрона. Это может

быть, например, атом углерода или атом кремния . Такой атом, как мы только что установили, может находиться в состояниях: 1S0 , 1D2 , . Какое из них основное? Согласно правилу Хунда основным будет состояние, соответствующееS= 1, т.е. один изP-термов. Т.к. оболочка 2p2 заполнена менее, чем наполовину, то . Таким образом, основной терм атома углерода и кремния 3P0.

20 (2). Магнитный момент атома.

В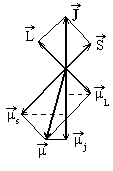ыше (в лекции 7) были рассмотрены орбитальныйμlи собственныйμsмоменты электрона. Сумма этих моментов определяет полный магнитный момент атома. Найдем этот момент с помощью векторной диаграммы. Изображая на векторной диаграмме магнитные моменты необходимо учесть, что гиромагнитное отношение для собственных моментов электрона вдвое больше отношения для орбитальных моментов Вследствие этого направление вектора полного магнитного момента атомаμ не совпадает с направлением полного механического моментаJ.

Сумма векторов LиSдает векторJ. Кроме механических моментов, электрон имеет и магнитные моменты: орбитальныйμl и собственныйμs, Направленные противоположно соответствующим механическим моментам. Если векторμl изобразить равным по длине векторуL, то в том же масштабе длина вектораμsдолжна быть в два раза больше длины вектораS. Из-за этого, как сказано выше, направление вектора полного магнитного моментаμ не совпадает с направлениемJ.

На полуклассическом языке можно сказать, что векторы LиS, а вместе с ними векторыμl иμs, прецессируют (вращаются) вокруг вектораJ. Поэтому средние значения проекций, перпендикулярных кJ, равны нулю (точнее говоря, эти проекции неопределенны), а определенное значение имеет только одна проекция вектораμ -проекцияμj на направление вектораJ. Эта величина называется эффективным полным магнитным моментом атома.

Найдем эту величину, для чего сложим проекции векторов μl иμsна направлениеJ:

Для определения косинусов воспользуемся теоремой косинусов из элементарной геометрии

Аналогично

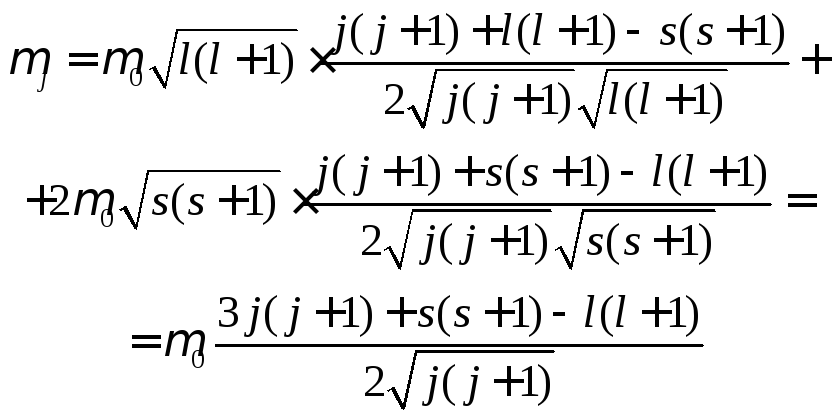
Поэтому

Умножим числитель и знаменатель последней дроби на

:

Обозначим выражение, стоящее в фигурных скобках: (20.1)

Эта величина называется множителем (фактором) Ланде (LandeA.) и определяет гиромагнитное отношение для эффективного полного момента атома.

Итак, эффективный магнитный момент атома равен: (20.2) а гиромагнитное отношение дляμj : (20.3)

Если поместить атом в магнитное поле то он будет вести себя как диполь с моментомμj, причем ориентация этого момента будет определяться проекциями вектораJна направление магнитного поля:

Чтобы найти воспользуемся формулами (17.5) и (17.6). Согласно формуле (17.5), проекция моментаJна направлениеBравна где магнитное внутреннее квантовое число принимает значения:

Сдругой стороны, ту же проекцию можно выразить с помощью косинуса угла между векторамиJиB:

отсюда

Таким образом, проекция эффективного магнитного момента атома на направление внешнего магнитного поля равна:

(20.4)

Отсюда можно найти потенциальную энергию взаимодействия магнитного момента атома с внешним магнитным полем: (20.5)

Эта энергия зависит от величины фактора Ланде g, определяемого формулой (20.1), и принимает ряд дискретных значений, определяемых магнитным внутренним квантовым числомmj.

Полученный результат легко обобщить на магнитный момент многоэлектронного атома. Как было отмечено выше, для большинства атомов имеет место нормальная (LS) связь между электронами, поэтому магнитный момент многоэлектронного атома равен сумме орбитальных и спиновых моментов электронов:

При помощи векторной диаграммы аналогично тому, как это было сделано для одного электрона, можно показать, что эффективный магнитный момент атома равен где множитель Ланде

авнутреннее квантовое числоJпринимает значения

В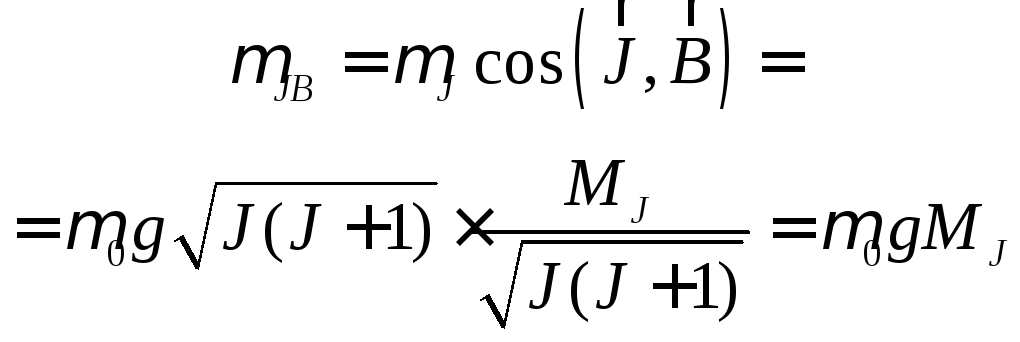о внешнем магнитном полеBвекторμJ может ориентироваться относительно этого поля только так, что его проекция на направлениеBравна

(20.6)

где MJ(аналог числаmj) принимает значения: (всего 2J+1 значений)

Следствием принципа Паули является то, что у любой полностью заполненной (замкнутой) оболочки суммарные орбитальный, спиновый и полный моменты импульса равны нулю:

Действительно, т.к. ms= ±1/2,m= 0, ±1, ±2, …, ±l, то для замкнутой оболочки ∑ml= 0 и ∑ms= 0, т.к. суммирование ведется по всем электронам. Отсюда следует, что и магнитный момент замкнутой оболочки равен нулю. Поэтому и механический, и магнитный моменты атома определяются лишь электронами, находящимися в незаполненных оболочках (валентными электронами).