16 (0). Строение электронных оболочек. Объяснение периодической системы д.И.Менделеева.

В 1869г. Д. И. Менделеевым был открыт периодический закон и построена периодическая система элементов, объяснение которой – одна из важнейших задач атомной физики.

Сформулируем прежде всего те принципы, на которых основано это объяснение:

1). Состояние электрона в атоме полностью определяется четырьмя квантовыми числами:

главным квантовым числом n= 1, 2, 3, …; орбитальным квантовым числом l = 0, 1, …,n-1; магнитным квантовым числомm = 0, ±1, ±2, …, ±l; магнитным спиновым квантовым числомms= +1/2, -1/2.

2) Принцип Паули: В атоме может существовать только один электрон в состоянии, характеризуемом данными значениями четырех квантовых чисел; т.е. два электрона в одном и том же атоме должны различаться значениями по крайней мере одного квантового числа.

3) Атом (как и любая система) устойчив тогда, когда находится в состоянии с наименьшей возможной энергией.

Совокупность электронов, обладающих одинаковым главным квантовым числом образует слой. Слои имеют названия :

Совокупность электронов, имеющих одинаковые nи l, образуетоболочку. Названия оболочек :

Принцип Паули ограничивает число электронов на той или иной электронной оболочке. Действительно, электроны в невозбужденном атоме стремятся перейти в состояние с наименьшей энергией (в устойчивое состояние), которое соответствует минимальным значениям главного и орбитального чисел. Однако возможность такого перехода ограничена принципом Паули. Поэтому электроны в невозбужденном атоме находятся в таких состояниях, при которых энергия атома является наименьшей, но распределение по состояниям удовлетворяет принципу Паули.

Установим теперь, сколько электронов может находится на оболочке и в атоме.

Т.к. число msможет иметь два значения, то в атоме может быть два электрона с одинаковыми числамиn, l, m. При заданномlквантовое числоmможет иметь (2l+1) значений, следовательно, на оболочке может быть 2(2l+1) электронов, т.е.

При заданном nквантовое число l может приниматьnзначений: 0, 1, 2, …,n-1. Поэтому максимальное число электронов в слое можно выразить суммой арифметической прогрессии:

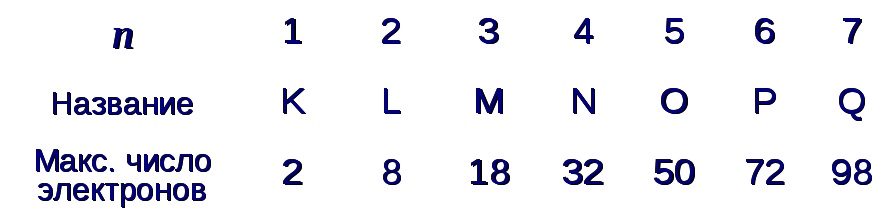
(16.1)

Конфигурация электронных оболочек атомов записывается с помощью следующих обозначений. Каждая оболочка обозначается соответствующим nи буквой, обозначающейl, а индексом справа вверху обозначается число электронов. Например:

Водород 1s1

Гелий 1s2

Литий 1s22s1

Углерод 1s22s22p2

Кислород 1s22s22p4

Аргон 1s22s22p63s23p6

Итак, принцип Паули дает следующую картину построения электронной оболочки атомов. Каждый вновь присоединяемый электрон связывается в состоянии с наименьшими возможными квантовыми числами. Эти электроны постепенно заполняют слой с одним и тем же главным квантовым число n. Когда построение слоя заканчивается, получается устойчивая структура (инертный газ). Следующий электрон начинает заполнение уже нового слоя и т.д. Эта идеальная схема соблюдается до 18 элемента таблицы Менделеева (до аргона). Начиная с 19-го элемента (калия) наблюдаются отступления от идеальной схемы. Причина этих отступлений заключается в том, что идеальная схема не учитывает взаимодействия электронов между собой.

Например, 19-ый электрон калия должен (согласно идеальной схеме) находиться в 3d-оболочке. Однако химические и спектроскопические данные указывают на то, что этот электрон находится в 4s-оболочке. Детальный расчет с учетом взаимодействия электронов показывает, что состояние 3dдействительно отвечает большей энергии, чем 4s. По этой же причине 20-ый электрон кальция тоже присоединяется в 4s-состояние, а нормальное заполнение 3d-оболочки начинается у скандия. Аналогичное нарушение нормального порядка наблюдается у рубидия, цезия, франция. Другое отступление от нормального порядка заполнения слоев имеет место у редких земель (Z=58 - 71): идет заполнение 4f-оболочки после того, как заполнены оболочки 5s, 5pи 6s.

Таким образом, атомная физика полностью объяснила периодическую таблицу элементов. Причем теория не только объяснила, но и уточнила таблицу. До 1922г. элемент Z=72 не был известен. Он был предсказан Менделеевым, и ему было оставлено место в группе редких земель. Однако по теоретическим соображениям, группа редких земель должна содержать 14 элементов (т.к. на 4fоболочке может находиться 14 элементов), т.е. должна заканчиваться 71-м элементом, а элементZ=72 должен быть аналогом циркония и титана. На это впервые указал Н. Бор, и вскоре элемент 72 (гафний) был открыт в циркониевых рудах и по своим химическим и оптическим свойствам оказался аналогом титана и циркония, а не элементов группы редких земель.

17(1). Полный момент импульса электрона в атоме. Символические обозначения термов. Правила отбора для оптических переходов.

Операции с векторами LиSможно производить с помощью следующего полуклассического метода. Вектора складываются по обычным правилам параллелограмма:

J = L + S, (17.1)

врезультате получается векторJ- вектор полного момента импульса. В это чисто классическое правило вносятся следующие поправки, характерные для квантовой механики. Во-первых, углы между векторамиLиSне могут быть произвольными. ВекторLможет располагаться относительно вектораJтолько под такими углами, чтобы его проекция на направлениеJ была равна , гдеm= 0, ± 1, …, ±l. Аналогичное требование предъявляется и к ориентации вектораS: его проекция на направлениеJ равна , гдеms= ±1/2. Таким образом, угол междуLиSможет принимать ряд дискретных значений.

Во-вторых, полный моментJ, как всякий момент импульса в квантовой механике имеет свое квантовое числоj, такое, что (17.2)

Числоjназываетсявнутренним квантовым числом, оно может принимать значения:

(17.3)

Формула (17.3) записана в общем виде для любой величины вектораS. Если рассматривается всего один электрон, тоs=1/2, и тогдаjможет принимать всего два значения: и (17.4)

Проекция вектораJна какое либо направлениеZ(ось квантования, направление внешнего магнитного или электрического поля и т.д.) в соответствии с законами квантовой механики равна: (17.5)

где (17.6)

т.е. mjможет принимать (2j+ 1) значений. Числоmjназываетсямагнитным внутренним квантовым числом. Еслиj- полуцелое число, то в этом случаеmjне принимает значение 0.

Эти правила сложения векторов LиS составляютвекторную модель атома, имеющую большое практическое значение: модель проста и наглядна, а ее результаты совпадают с экспериментом и с результатами точного квантовомеханического решения.

Различные состояния атома (термы) принято обозначать специальными символами, по которым сразу можно указать все квантовые числа. Общий вид такого обозначения: (17.7)

где квантовое число Lобозначает орбитальный момент всего атома (так же, как и для отдельного электрона):L= 0 1 2 3 4 …

Символ SPDFG…

Справа внизу записывается квантовое число полного момента атома, слева вверху – кратность (мультиплетность) терма: (17.8) гдеS– спиновое квантовое число всего атома.

Т.к. терм - это характеристика всего атома, то используются прописные буквы вместо строчных (которые применяются для отдельного электрона). Примеры:

Запись (читается "дублет Р три вторых") означает, что L= 1,S= 1/2,J= 3/2.

Запись (читается "синглетSноль") означает, чтоL= 0,S= 0,J= 0.

Запись (читается "триплет Dдва") означает, чтоL= 2,S= 1,J= 2.

Правила отбора для оптических переходов

Согласно комбинационному принципу, волновое число любой спектральной линии (в испускании и поглощении) может быть представлена как разность двух термов (17.9)

Но обратное утверждение не всегда справедливо: не всякая комбинация термов дает частоту, сjответствующую реально наблюдаемой спектральной линии. Существуют определенные правила отбора, указывающие, какие комбинации термов возможны, какие нет (точнее маловероятны или даже имеют нулевую вероятность).

Эти правила связаны с законами сохранения момента импульса и четности в квантовых переходах. В частности установлено, что в атоме наиболее вероятны переходы между состояниями, при которых квантовые числаl иmменяются на величину: (17.10)

причем правило отбора для магнитного квантового числа mнадо учитывать только в том случае, если атом находится в магнитном поле. На главные квантовые числаn1 иn2 никаких ограничений не накладывается, т.е. величина ∆nможет быть любой.

Если условие (17.10) соблюдается, то такие переходы называются разрешенными. Другие переходы маловероятны, и их называют запрещенными. Другими словами, разрешены переходы между соседними по lуровнями, т.е. междуs- иp-состояниями, междуp- иd-состояниями, междуd- иf-состояниями и т.д.

Интенсивность спектральной линии определяется вероятностью перехода электрона из одного состояния в другое. В теории Бора это можно было представить наглядно в виде пространственного перемещения электрона с одной орбиты на другую. В квантовой теории никаких орбит нет, а переход связан с представлением об изменении волновой функции.

Вероятность перехода определяется так называемым матричным элементом: интегралом вида

(17.11)

который представляет собой дипольный момент ex, усредненный между состояниямиYmиYn. Вычисления этого элемента и приводят к сформулированным выше правилам отбора. Отметим еще раз, что правила отбора имеют вероятностный характер: "запрещенные" спектральные линии иногда можно наблюдать, но они имеют малую интенсивность.