
- •Физика атома, атомного ядра и элементарных частиц
- •С точки зрения классической физики альфа-распад невозможен
- •Альфа-распад - это следствие волновых свойств микрочастиц, одно из прояв- лений туннельного эффекта.
- •Для барьера прямоугольной формы коэффициент прозрачности был най- ден выше (формула (10.13):
- •Барьер произвольной формы достаточно представить в виде последовательности узких прямоугольных барьеров. Тогда
- •Применительно к альфа-распаду:
- •После ряда преобразований находим:
- •Чтобы найти постоянную распада, надо оценить
- •Тогда, логарифмируя формулу (32.4), находим:
- •Можно объяснить и узкие границы для значений кинетической энергии альфа- частиц. При энергии

Физика атома, атомного ядра и элементарных
ядра и элементарных  частиц
частиц
32.(2). Теория альфа-распада.
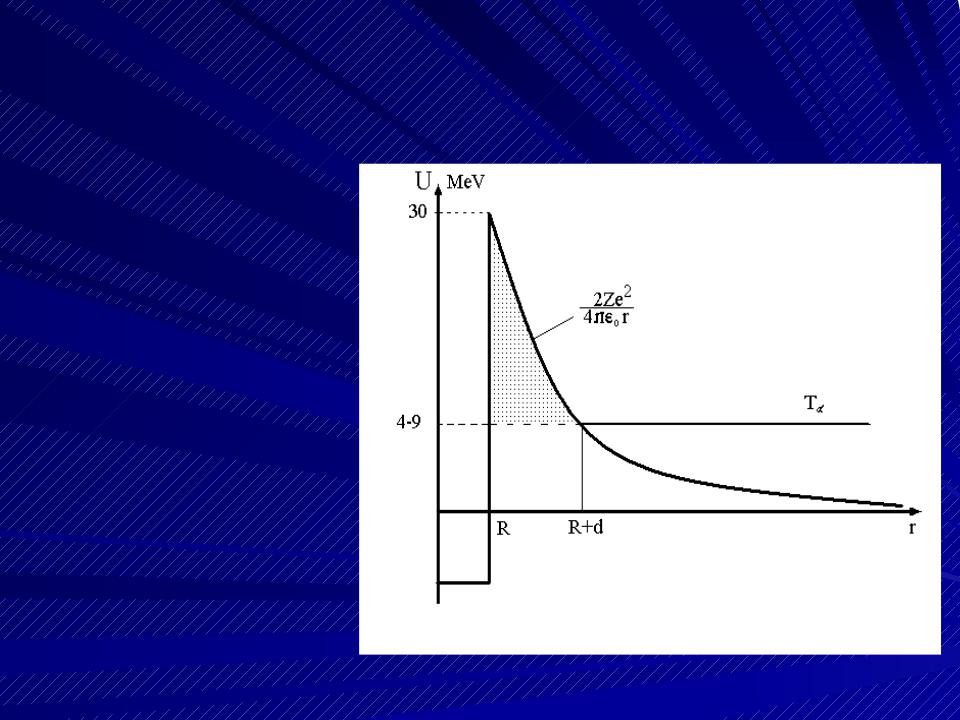
С точки зрения классической физики альфа-распад невозможен
Высота потен- циального барьера больше кинетичес- кой энергии альфа- частицы.

Альфа-распад - это следствие волновых свойств микрочастиц, одно из прояв- лений туннельного эффекта.
Туннельным эффектом называется явле- ние прохождения частицы сквозь потен- циальный барьер; при этом частица не теряет энергию, и выходит из барьера с  той же энергией, с какой в него попа- дает.
той же энергией, с какой в него попа- дает. 

Для барьера прямоугольной формы  коэффициент прозрачности был най- ден выше (формула (10.13):
коэффициент прозрачности был най- ден выше (формула (10.13):
D 16E |
|
|
E |
|
2 |
2m(U0 E)d |
1 |
e h |
|
||||
U0 |
|
|
U0 |
|
|
|
|
|
|
|
|
||
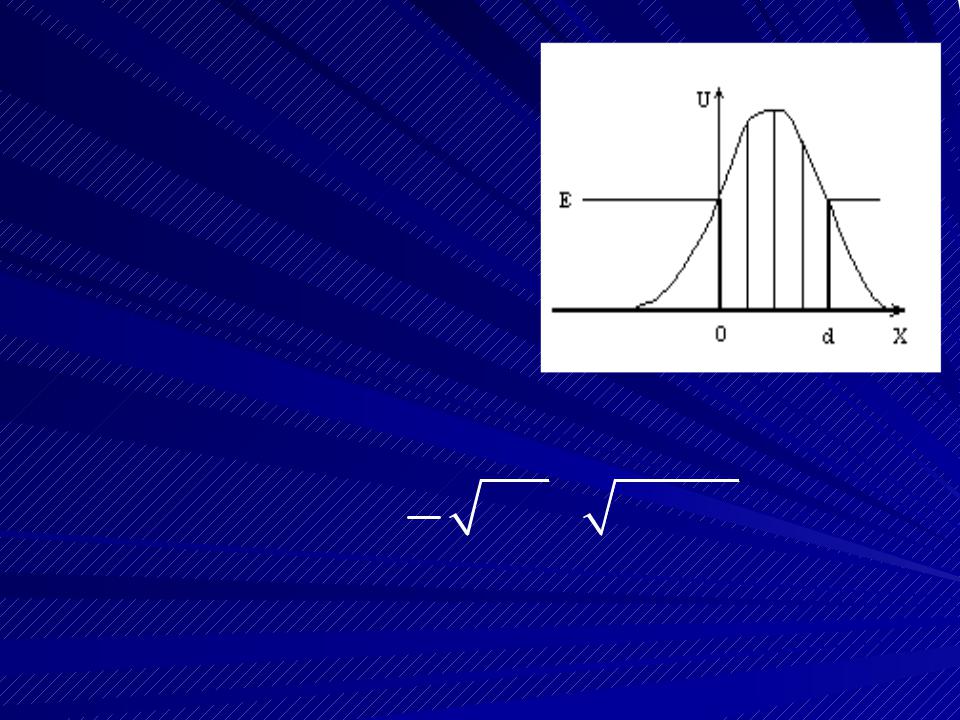
Барьер произвольной формы достаточно представить в виде последовательности узких прямоугольных барьеров. Тогда
|
|
2 |
d |
|
|
|
|||
D exp |
h |
2m U Edx |
||
|
|
0 |
|
|

Применительно к альфа-распаду:
|
|
2 |
|
R d |
2Ze2 |
|
|
|
|
D exp |
2m |
|
T dr |
|
|||||
|
|
|
|
|
|
||||
|
|
h |
|
4 |
r |
|
(32.1) |
||
|
|
|
|
|
|||||
|
|
|
|
||||||
|
|
|
R |
0 |
|
|
|
||
|
|
|
|
|
|
|
|
|
|
Интеграл вычисляется подстановкой
y2 |
2Ze2 |
T |
|
4 0r |
|
||
|
|
(32.2) |
|
|
|

После ряда преобразований находим:
|
Ze |
2 |
|
2m |
|
2 0 RT |
|
|
arccos |
||||
D exp |
0h |
|
T |
Ze2 |
||
|
|
|
||||
|
|
|
|
|
|
|
|
2 0 RT 1 |
||
|
Ze |
2 |
|
|
|
|
|
2 0 RT
Ze2
(32.3)

Чтобы найти постоянную распада, надо оценить
предэкспоненциальный множитель. По физи- ческому смыслу рассматриваемой модели, это должна быть частота , с которой альфа-час- тица, двигаясь внутри ядра, ударяется о его внутренние стенки: = v/2R, где v - средняя скорость альфа-частицы, которую можно оценить из соотношения неопределенности 2Rmv = h. Тогда постоянную распада можно  представить в виде:
представить в виде: 
D |
h |
e |
(32.4) |
|
mR2 |
|
|

где |
|
2 |
|
2marccos |
2 0 RT |
|
2 0 RT 1 2 0 RT |
|
||||||||
Ze |
|
|||||||||||||||
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
2 |
|
|
2 |
|
|
2 |
|
||
|
|
|
h |
|
T |
|
Ze |
|
Ze |
Ze |
|
|||||
|
|
|
|
|
|
|
|
|
|
|||||||
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
2Ze2 |
|
|
|
|
|
|
|||
т.к. |
|
|
|
|
T |
|
|
|
|
|
|
|
||||
|
|
|
|
|
4 0 R |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
то выражение для можно разложить в ряд и ог- раничиться первым приближением:
|
|
|
|
|
2 |
|
RT |
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
1, |
|
|
|
|
|
|
|
|
|
|
Ze |
2 |
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||
arc cos |
2 0 RT |
|
|
arcsin |
2 0 RT |
|
|
|
2 0 RT |
||||
Ze2 |
2 |
|
Ze2 |
2 |
Ze2 |
||||||||

Тогда, логарифмируя формулу (32.4), находим:
|
R 2mZe |
2 |
|
Ze |
2 |
|
h |
|
|
ln |
|
|
|
2 ln |
|
(32.5) |
|||
|
|
|
|
|
|
|
|||
|
h 0 |
|
|
2 0 RT |
|
|
2 |
|
|
|
|
2 |
|
mR |
|
||||
|
|
|
|
||||||
Таким образом, постоянную альфа-распада дей- ствительно можно представить в виде закона Гейгера-Неттола:
ln |
a |
b |
|
T |
|
|
|
|
