
ММС
.docx§ 9. Внутрифазные и межфазные взаимодействия в плотно упакованных зернистых, порошкообразных и пористых средах
Если
твердая фаза представляет плотную
упаковку дисперсных частиц, то в ней
может происходить перенос импульса за
счет непосредственного взаимодействия
между частицами, которое описывается
приведенным тензором напряжений
 .
Если пренебречь пульсационным переносом
импульса в фазах
.
Если пренебречь пульсационным переносом
импульса в фазах
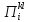 ,
что обычно можно делать в случае пористых
сред, то в соответствии с (1.3.25) тензор
напряжений в смеси и приведенные тензоры
напряжений в фазах
,
что обычно можно делать в случае пористых
сред, то в соответствии с (1.3.25) тензор
напряжений в смеси и приведенные тензоры
напряжений в фазах
 представляются в виде
представляются в виде
 =
= <
< +
+ <
< =
= +
+ ,
,

 =
=
 <
< +
+
 ,
,
 =
= <
< +
+ .
.
Тензор
напряжений в дисперсной фазе. Как и
ранее в § 4 для газовзвесей, можно считать,
что действие вязкости дисперсионной
(газовой или жидкой) фазы через межфазную
силу
Fμ
во много раз превышает действие вязкости
через тензоры напряжений
 <
< и
и
 в
виде слагаемого
в
виде слагаемого
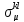 .
Поэтому примем
.
Поэтому примем
< =
—
=
—
 ,
,
 = —
= — =
—
=
—
 .
(1.9.2)
.
(1.9.2)
Выражение =
= соответствует случаю, когда межзеренные
контакты точечные, т. е. почти вся
поверхность зерен контактирует с газовой
или жидкой фазой. Таким образом, имеем
соответствует случаю, когда межзеренные
контакты точечные, т. е. почти вся
поверхность зерен контактирует с газовой
или жидкой фазой. Таким образом, имеем
 =
—
=
—
 +
+ ,
,
 <
< = —
= —
 +
+ .
(1.9.3)
.
(1.9.3)
Из
этих выражений следует, что приведенное
напряжение в дисперсной фазе
 определяется через непосредственно
измеряемые величины — полное напряжение
в смеси
определяется через непосредственно
измеряемые величины — полное напряжение
в смеси
 и
давление газа или жидкости в порах
и
давление газа или жидкости в порах
 .
Напряжение
.
Напряжение
 интерпретируется
как часть тензора напряжений <
интерпретируется
как часть тензора напряжений < в
твердой фазе или скелете, обусловленная
передачей усилий через контакты между
зернами. Если исключены контакты между
зернами, что имеет место в малоконцентрированных
(бесстолкновительных или бесконтактных)
дисперсных смесях, рассмотренных выше
в § 1—4, то
в
твердой фазе или скелете, обусловленная
передачей усилий через контакты между
зернами. Если исключены контакты между
зернами, что имеет место в малоконцентрированных
(бесстолкновительных или бесконтактных)
дисперсных смесях, рассмотренных выше
в § 1—4, то
 = 0. При наличии контактов между дисперсными
частицами (
= 0. При наличии контактов между дисперсными
частицами ( 0) дисперсную смесь будем называть
плотной, контактной или столкновительной.
(См. также В. Н. Николаевский и др., 1970.)
0) дисперсную смесь будем называть
плотной, контактной или столкновительной.
(См. также В. Н. Николаевский и др., 1970.)
Межфазная
сила.
Учитывая, что вся поверхность дисперсных
частиц (за исключением конечного числа
точек межзеренных контактов) контактирует
с газом, межфазную силу можно представить
так же, как и в бесконтактной дисперсной
смеси в виде (1.3.41), выделяя силу Архимеда
 и силу присоединенных масс
и силу присоединенных масс
 из-за
действия инерции и тяжести в несущей
фазе
из-за
действия инерции и тяжести в несущей
фазе
 =∇
=∇ +
+ +
+ +
+ ,
,
 =
= ,
,
 =
=
 ,
(1.9.4)
,
(1.9.4)
 =
= (
( —
—
 ),
),
где
 сила,
приходящаяся на одну частицу (зерно)
из-за вязкости дисперсионной фазы,
определяемая коэффициентом вязкого
взаимодействия
сила,
приходящаяся на одну частицу (зерно)
из-за вязкости дисперсионной фазы,
определяемая коэффициентом вязкого
взаимодействия
 ,
который задается аналогично (1.4.9);
,
который задается аналогично (1.4.9);
 —коэффициент,
учитывающий влияние неодиночности и
несферичности дисперсных частиц на
силу присоединенных масс
—коэффициент,
учитывающий влияние неодиночности и
несферичности дисперсных частиц на
силу присоединенных масс
(0 )-
Тогда аналогично (1.3.45) уравнения импульсов
фаз в контактной дисперсной смеси можно
записать в виде
)-
Тогда аналогично (1.3.45) уравнения импульсов
фаз в контактной дисперсной смеси можно
записать в виде
 (
( +
+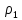 g,
g,
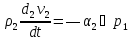 +
+ +
+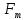 +
+ +
+ (
( +
+ g,
g,
(1.9.5)
 =
= ,
,
 =
=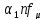 ,
—
,
— =
= =
nj.
=
nj.
Из этих уравнений нетрудно получить соответствующее выражение для удельной межфазной силы в дисперсной смеси
 =
= +
+ +
+
 (
( ,
(1.9.6)
,
(1.9.6)
 =
= ,
,
 =
= (
( ).
).
Рассмотрим
другую двухфазную структуру, состоящую
из пористой среды*), насыщенной жидкостью
или газовой фазой, которая занимает
поры в виде каналов. Такая структура
может рассматриваться как предельный
случай дисперсной структуры с наиболее
полными контактами между частицами
твердой фазы, когда площадь межзеренных
контактов сравнима с поверхностью
зерен. Эту предельную структуру с порами
в виде каналов будем называть «канальной
структурой». Для такой структуры тензоры
 ,
, сила f
и числовая концентрация частиц n
не имеют смысла, и выражения (1.9.1) и
(1.9.4) не могут быть использованы для
определения напряжений в фазах и силы
межфазного воздействия. Напряжение в
жидкой или газовой фазе зададим давлением
по тем же соображениям, что и в (1.9.2) и
аналогично (1.9.3) введем приведенный
тензор напряжений в твердой фазе
сила f
и числовая концентрация частиц n
не имеют смысла, и выражения (1.9.1) и
(1.9.4) не могут быть использованы для
определения напряжений в фазах и силы
межфазного воздействия. Напряжение в
жидкой или газовой фазе зададим давлением
по тем же соображениям, что и в (1.9.2) и
аналогично (1.9.3) введем приведенный
тензор напряжений в твердой фазе
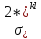 .
.
 =
—
=
— ,
,
 =
—
=
—
 ,
(1.9.7)
,
(1.9.7)
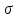 =
= +
+ =
—
=
—
 .
.
Видно,
что напряжения
 /
/ характеризуют отличие средних напряжений
характеризуют отличие средних напряжений
 в твердой фазе от давления в порах
в твердой фазе от давления в порах
 .
.
Если
каналы в пористой среде гладкие,
прямолинейные и ориентированы вдоль
относительного ускорения фаз, то в
межфазной силе
 нет составляющей за счет мелкомасштабных
пульсаций давления, возникающих в общем
случае из-за сил инерции в мелкомасштабном
движении, т. е.
нет составляющей за счет мелкомасштабных
пульсаций давления, возникающих в общем
случае из-за сил инерции в мелкомасштабном
движении, т. е.
 =
0 (см.( 1.2.46)).
=
0 (см.( 1.2.46)).
Тогда =
= +
+
 =
= =
=
 (
( ,
(1.9.8)
,
(1.9.8)
где
 — характерный радиус пор. В общем случае
— характерный радиус пор. В общем случае
 и межфазная сила определяется как
вязким, так и инерционным взаимодействием:
и межфазная сила определяется как
вязким, так и инерционным взаимодействием:
 =
=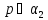 +
+ +
+ ,
,

 =
=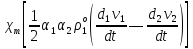 +
+ (
(
(0 )
, (1.9.9)
)
, (1.9.9)

 =
=
 (
( .
.
Это
выражение обобщает (1.9.6) и (1.9.8). Здесь
 и
и
 коэффициенты инерционного и вязкого
взаимодействия фаз, зависящие от
структуры среды, причем разреженной
дисперсной смеси с частицами радиусом
коэффициенты инерционного и вязкого
взаимодействия фаз, зависящие от
структуры среды, причем разреженной
дисперсной смеси с частицами радиусом
 соответствует
соответствует
 = 1 и
= 1 и
 =
= ,
а
пористой среде c прямолинейными
цилиндрическим каналами радиусом
,
а
пористой среде c прямолинейными
цилиндрическим каналами радиусом
 ,
ориентированными вдоль направления
относительного движения и ускорения
фаз, соответствует
,
ориентированными вдоль направления
относительного движения и ускорения
фаз, соответствует
 = О
= О
и
 = 8
= 8 .
.
В результате обобщения (1.9.5) на пористые и зернистые среды имеет вид
 =
—
=
— —
— —
— +
+
 (
( )
+
)
+
 g,
(1.9.10)
g,
(1.9.10)
 =
—
=
— —
— +
+ +
+ +
+ g
,
g
,
где
 и
и
 определяются
выражениями(1.9.9).
определяются
выражениями(1.9.9).
Сила
трения в зернистах средах определяется
так же, как и для газовзвесей (см. (1.3.42),
(1.4.9)) с помощью коэффициента трения
 .
Для этого коэффициента имеем следующие
эмпирические формулы:
.
Для этого коэффициента имеем следующие
эмпирические формулы:
 =
= ,
0.88
,
0.88 0.45,
0.45,
 =
=
 =
= +
+
 +
0.42 ,
+
0.42 ,
 0.08,
(1.9.11)
0.08,
(1.9.11)
 =
=
 =
=
 .
.
Здесь
 получено из обработки экспериментов
по стационарной продувке газов сквозь
насыпной слой (разной пористости)
неподвижных сферических частиц (S.
Ergun,
1952);
получено из обработки экспериментов
по стационарной продувке газов сквозь
насыпной слой (разной пористости)
неподвижных сферических частиц (S.
Ergun,
1952); соответствует одиночной частице или
газовзвеси, когда объемная концентрация
частиц
соответствует одиночной частице или
газовзвеси, когда объемная концентрация
частиц
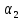 мала. В промежуточной области
мала. В промежуточной области
 здесь предлагается использовать линейную
интерполяцию с
здесь предлагается использовать линейную
интерполяцию с
 и
и
 .
.
Работа
поверхностных сил.
Уравнения
притока тепла.
Работа внешних поверхностных сил
 определяется
вектором c,
который, обобщая (1.1.58) и (1.3.37), зададим в
виде
определяется
вектором c,
который, обобщая (1.1.58) и (1.3.37), зададим в
виде
 =
=
 +
+
 = —
= — (
( +
+
 ) +
) +
 .
(1.9.12)
.
(1.9.12)
Аналогично(1.1.43) нетрудно показать, что в соответствии с уравнениями импульсов фаз (1.9.10) на изменение кинетической энергии идет работа,
— ( +
+
 )
) +
+
 , (1.9.13)
, (1.9.13)
а
остальная часть
 ,
равная
,
равная
—
 (
( +
+
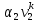 ) +
) +
 ,
(1.9.14)
,
(1.9.14)
идет на изменение внутренних энергий фаз в соответствии с уравнениями притока тепла фаз
 =
=
 + (
+ ( )(
)( )
+
)
+ (
( —
— )
+
)
+
 ,
,
 =
=
 +
+
 —
—
 (
( —
— )
+
)
+
 ,
(1.9.15)
,
(1.9.15)
 +
+ = —
= —
 (
( —
— )
.
)
.
При сопоставлении этих уравнений с (1.9.14) следует иметь в виду, что в соответствии с уравнениями сохранения масс фаз имеет место
 +
+
 —
— =
—
=
—
 (
(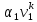 +
+
 ). (1.9.16)
). (1.9.16)
Деформация
(как сдвиговая, так и объемная) пористого
тела сопровождается эффектами вязкости,
упругости и пластичности, описание
которых связано с разделением уравнения
для внутренней энергии твердой фазы
(второе уравнение (1.9.15)) на два уравнения:
уравнение для упругой энергии и уравнение
для тепловой энергии. Это связано с тем,
что внутренняя энергия конденсированной
фазы складывается из упругой
 и тепловой и
и тепловой и составляющих (см. также § 1 гл. 3)
составляющих (см. также § 1 гл. 3)
 =
= +
+ ,
,
 =
=
 (
( ,
,
 ,
,
 ),
(1.9.17)
),
(1.9.17)
 (
( —
—
 +
+ ,
,
где
 ,
,
 —
второй и третий инварианты тензора
деформаций второй фазы*), определяемого
эволюцией поля скоростей
—
второй и третий инварианты тензора
деформаций второй фазы*), определяемого
эволюцией поля скоростей
 (t,
x).
(t,
x).
При
не очень высоких давлениях деформация
твердой фазы, описываемая полем скоростей
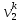 ,
происходит в основном за счет переупаковки
зерен и изменения объемов пор, ибо
сжимаемость и сдвиговые деформации
материала твердой фазы очень малы, в
частности можно считать
,
происходит в основном за счет переупаковки
зерен и изменения объемов пор, ибо
сжимаемость и сдвиговые деформации
материала твердой фазы очень малы, в
частности можно считать
 const.
В
этом случае упругая внутренняя энергия
не меняется, вся деформация твердой
фазы является необратимой и вся работа
соответствующих внутренних межгранулярных
сил
const.
В
этом случае упругая внутренняя энергия
не меняется, вся деформация твердой
фазы является необратимой и вся работа
соответствующих внутренних межгранулярных
сил
 =
=
 диссипируется в тепловую. Такой ситуации
соответствует используемая в механике
грунтов модель пластического газа (X.
А. Рахматулин и др., 1961), которая для
одномерного случая движения рассмотрена
в § 4 гл. 3.
диссипируется в тепловую. Такой ситуации
соответствует используемая в механике
грунтов модель пластического газа (X.
А. Рахматулин и др., 1961), которая для
одномерного случая движения рассмотрена
в § 4 гл. 3.
Как
и межфазное трение межфазный стационарный
теплообмен в насыпных слоях, определяемый
величиной
 =
=
 , описывается с помощью числа
, описывается с помощью числа
 ,
как и в газовзвесях (см. (1.3.56), (1.4.11)), для
которого имеются следующие эмпирические
формулы (А. Ф. Чудновский, 1954) :
,
как и в газовзвесях (см. (1.3.56), (1.4.11)), для
которого имеются следующие эмпирические
формулы (А. Ф. Чудновский, 1954) :
 =
=

§ 10. Уравнения механики двухфазной упругопластической
сплошной среды в односкоростном, однотемпературном
и с общим давлением фаз приближении
Рассмотрим движение двухфазной среды, когда можно пренебречь относительным движением фаз и несовпадением их температур, т. е. можно использовать так называемое односкоростное и однотемпературное приближение. Как уже указывалось, эффекты движения фаз с разными скоростями часто являются несущественными при интенсивных течениях пузырьковых газойли парожидкостных смесей. Кроме того, в смесях конденсированных фаз (композиционные материалы, двухфазные смеси, которые возникают из-за полиморфных превращений в твердых телах, инициируемых сильными ударными волнами (см. гл. 3)) часто силы межфазного взаимодействия и сцепления, а также интенсивности межфазного теплообмена на границах зерен, включений, волокон настолько велики, что средним смещением фаз друг относительно друга и несовпадением их средних температур можно пренебречь Далее, в отличие от предыдущих параграфов, дан вывод основных уравнений в лагранжевых переменных. Их использование позволяет проще реализовать численное решение одномерных задач о движении односкоростной среды с контактными границами.
Уравнения
сохранения двухфазной среды в
односкоростном приближении в лагранжевых
переменных.
Выведем дифференциальные уравнения
сохранения масс фаз, импульса и энергии
двухфазной смеси в лагранжевых декартовых
координатах
 (к
= 1, 2, 3), так что r
(
(к
= 1, 2, 3), так что r
( ,
,
 ,
,
 )
определяет положение частицы среды в
начальный момент времени. Текущее
положение частицы среды определяется
ее эйлеровыми координатами
)
определяет положение частицы среды в
начальный момент времени. Текущее
положение частицы среды определяется
ее эйлеровыми координатами
 или
концом вектора x(
или
концом вектора x( ,
,
 ,
,
 ),
для которых имеется уравнение перемещения
),
для которых имеется уравнение перемещения
 =
=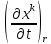 =
= (r, t). (1.10.1)
(r, t). (1.10.1)
Заметим,
что здесь частная производная по времени
 /
/ t
берется при фиксированных лагранжевых
координатах, т. е. вдоль траектории
материальной частицы, и поэтому здесь
t
берется при фиксированных лагранжевых
координатах, т. е. вдоль траектории
материальной частицы, и поэтому здесь
 /
/ t
— субстанциональная производная
t
— субстанциональная производная

 .
(1.10.2)
.
(1.10.2)
Пусть I (r, t ) —степень расширения среды, или якобиан преобразования от лагранжевых к эйлеровым координатам
I=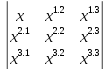
 (1.10.3)
(1.10.3)
определяющий отношение текущего элементарного объема dV выделенной
вокруг
точки частицы к ее объему
 в
начальный момент времени:
в
начальный момент времени:
I=
dV
/ ( 1.10.4)
( 1.10.4)
Пусть
 (r)
= р(0, r)—
плотность среды в начальный момент
времени t
= 0. Тогда закон сохранения массы смеси
имеет вид ρ
dV
=
(r)
= р(0, r)—
плотность среды в начальный момент
времени t
= 0. Тогда закон сохранения массы смеси
имеет вид ρ
dV
=
 dVo,
или
dVo,
или
ρI
=
 , (1.10.5)
, (1.10.5)
а
уравнения сохранения масс фаз с учетом
фазовых переходов, характеризуемых их
интенсивностью
 ,
отнесенной, в отличие от
,
отнесенной, в отличие от
 ,
к единице объема среды в начальный
момент времени, записываются в виде
,
к единице объема среды в начальный
момент времени, записываются в виде
 (
( dv)
= —
dv)
= — ,
,
 (
( dv)
=
dv)
=
 (
( ),
),
где
 —
интенсивность фазовых переходов,
отнесенная к единице текущего объема
среды. Разделив обе части этих уравнений
на
—
интенсивность фазовых переходов,
отнесенная к единице текущего объема
среды. Разделив обе части этих уравнений
на
 ,
получим
,
получим
 (
( I)
= —
I)
= —
 ,
,
 (
( I)
=
I)
=

 (1.10.6)
(1.10.6)
Запишем
уравнение сохранения импульса для массы
среды, находящейся в начальный момент
времени в объеме
 ,
ограниченном поверхностью δ
,
ограниченном поверхностью δ :
:
 (
(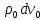 )
=
)
=
 =
= d
d +
+
 g,
g,
где
 =
=
 — тензор напряжений Лагранжа, который,
в отличие от до сих пор используемого
тензора напряжений Эйлера
— тензор напряжений Лагранжа, который,
в отличие от до сих пор используемого
тензора напряжений Эйлера
 ,
определяет интенсивность поверхностных
сил, отнесенных не к текущему, а к
начальному размеру и положению сечения
d
,
определяет интенсивность поверхностных
сил, отнесенных не к текущему, а к
начальному размеру и положению сечения
d с единичной нормалью
с единичной нормалью
 ;
g — интенсивность внешних массовых сил,
отнесенных к единице массы среды.
Используя теорему Гаусса — Остроградского,
получим
;
g — интенсивность внешних массовых сил,
отнесенных к единице массы среды.
Используя теорему Гаусса — Остроградского,
получим
 =
=
 +
+
 g
g . (1.10.7)
. (1.10.7)
Внутреннюю энергию смеси будем считать аддитивной по внутренним энергиям фаз, тем самым пренебрегая особыми свойствами слоев вещества, прилегающих к границам зерен или межфазных границ
