Раздел 1. Формальные грамматики
Лекция 2.
Тема лекции. Способы определения языковых процессоров. Формальные грамматики. Классификация грамматик.
Язык, порождаемый грамматикой. Левосторонний и правосторонний выводы. Дерево вывода.
-
Формальные грамматики.
В предыдущем разделе был определен язык, как множество строк, содержащих символы некоторого алфавита. Для практического использования такого языка кроме символов алфавита необходимо знать синтаксис и семантику языка. Под синтаксисом понимают синтаксические определения, которые точно устанавливают какие строки имеют смысл в данном языке. Эти определения дают правила построения допустимых в языке конструкций слов, групп слов и предложений, образуемых из символов алфавита. Под семантикой языка понимают правила интерпретации синтаксических определений, задающие смысл допустимым конструкциям языка. Для описания синтаксиса языков программирования используются формулы Бэкуса - Наура и синтаксические диаграммы. Универсальным способом описания являются формальные грамматики. Грамматика представляет собой математическую систему, порождающую язык. Строки языка строятся способом, точно определенным правилами грамматики.
Формальная
грамматика
- это четверка
где
- конечное множество нетерминальных
символов (нетерминалов);
- конечное, не пересекающееся с
,
множество терминальных
символов (терминалов),
;
- конечное множество правил-продукций
вида
,
где
- строка левой части продукции
,
- строка правой части продукции
,
другими словами
,
,
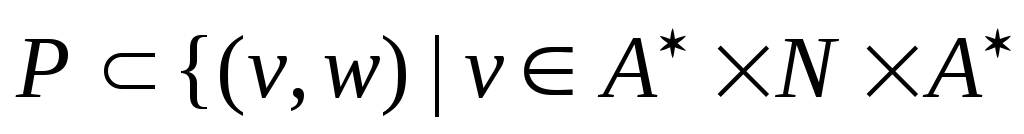где
;
- начальный символ грамматики
.
Символ
в продукции
означает возможность замены строки
на строку
.
В качестве примера рассмотрим следующую
грамматику
,
где множество
содержит следующие продукции
Для сокращения
записи множества продукций сгруппируем
продукции, имеющие совпадающие левые
части. Правые части этих продукций будем
записывать в одну строку, разделяя их
символом "|". При такой форме записи
множество продукций грамматики
будет выглядеть следующим образом
Грамматика
рекурсивным образом определяет
порождаемый язык, который содержит
множество выводимых из начального
символа строк. Определим формально
выводимую строку для грамматики
.
Строка
называется выводимой
строкой
грамматики
,
если
продукция из множества
и
строка терминальных и нетерминальных
символов длиной 1
[2]. Выводимая строка получается путем
замены строки
на строку
в строке
.
Такое преобразование строки записывают
в виде
Преобразование
можно рассматривать как отношение на
множестве
[1,4]. Это отношение является рефлексивным,
так как допустима замена строки
на самое себя. Однако оно определено не
для всех элементов
, нетранзитивно
и несимметрично.
Отношение
на множестве
задается как
,
если существует последовательность
для
и
.
В этом случае говорят, что строка
выводится из строки
за один более шагов. Отношение
рефлексивно
и транзитивно, но несимметрично. Если
строка
является выводимой из начального символа
строкой (
),
то ее называют сентенциальной
формой. Не
содержащая нетерминальных символов
сентенциальная форма называется
предложением
(или сентенцией).
Множество всех предложений грамматики
называют языком, порождаемым этой
грамматикой и обозначают
.
Таким образом
Может так случиться,
что две грамматики
и
порождают один и тот же язык
.
О таких грамматиках говорят, что они
эквивалентны.
В дальнейшем в тех примерах, где ясно о
какой грамматике идет речь , в обозначениях
вида
и
символ грамматики
будем опускать.
Рассмотрим примеры
предложений нескольких языков. Для
приведенной выше грамматики
в язык включены следующие предложения,
представляющие собой восьмеричные
числа.
2 вывод 
23 вывод 
(правило
)
(правило
)
(правило
)
(правило
)
637 вывод 
В предложенной
грамматике левые части всех продукций
содержали только по одному символу. В
следующей грамматике
продукции в левой части содержат строки,
состоящие более чем из одного символа.
В грамматике
из начального символа можно вывести
строку вида
.
Например, строку
(правило
)
(правило
)
(правило
)
(правило
)
(правило
)
(правило
)
2.2. Классификация грамматик.
По виду порождающих
правил, а точнее строк
и
в правой и левой частях продукций
множества
грамматики
последняя может относиться к одному из
четырех типов грамматик.
Грамматика
называется :
-
праволинейной или автоматной (тип 3), ес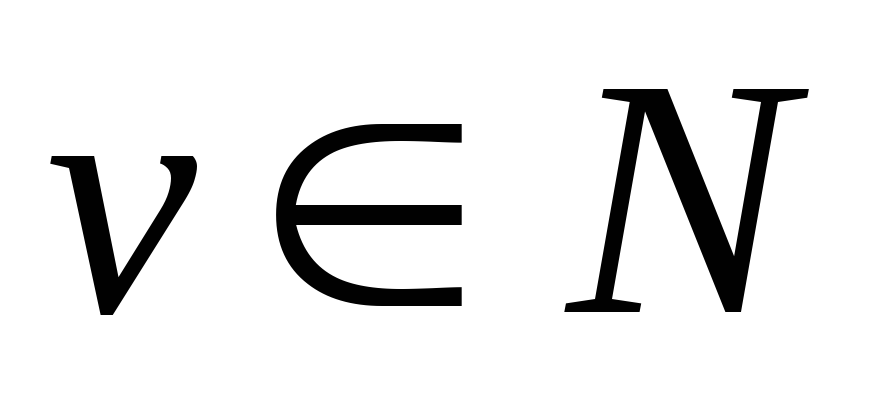ли
,
или
,
т.е. каждое правило из множества продукций
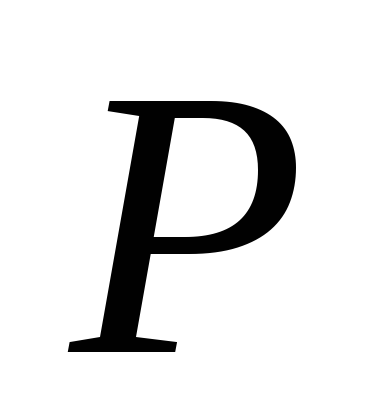имеют вид
,
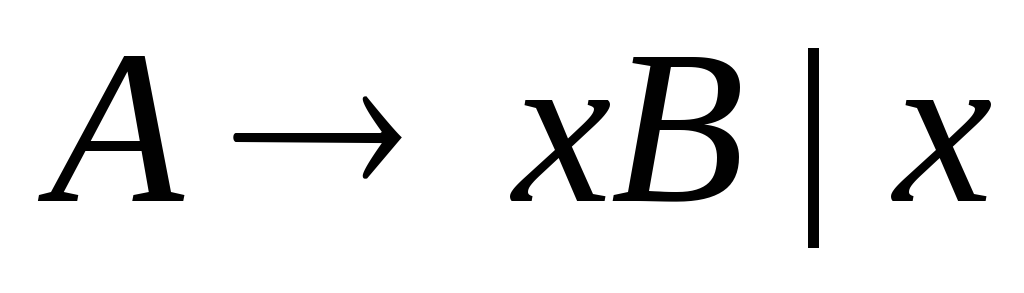где
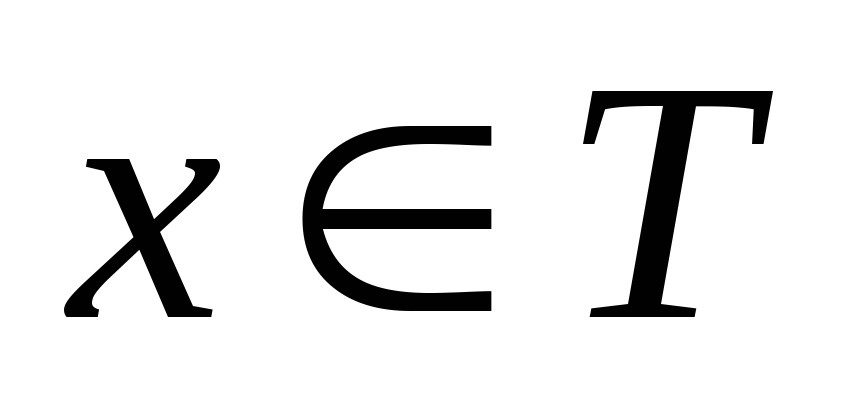и
-
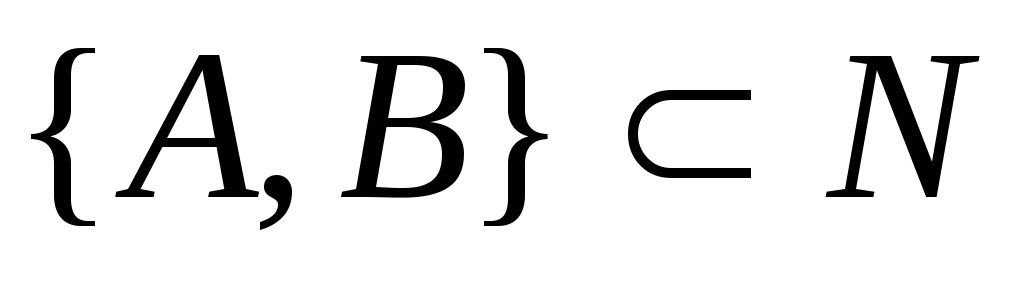
контекстно-свободной (тип 2), если
,
; -
контекстно-зависимой неукорачивающей (тип 1), если
,
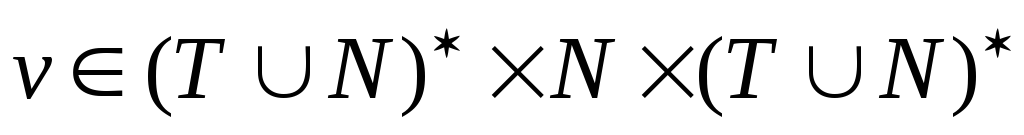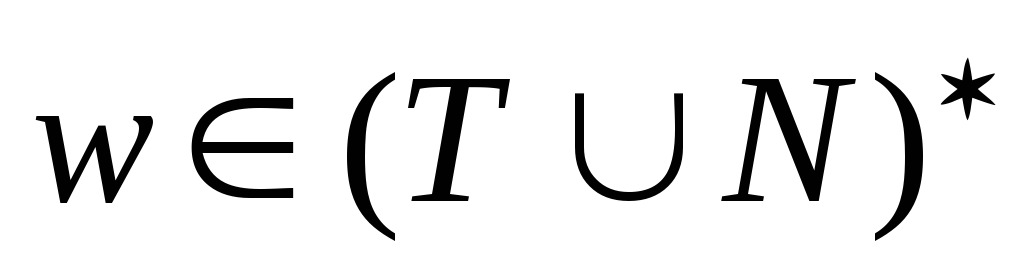и длина строки
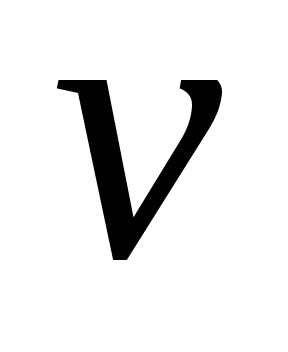не превышает длину строки
; -
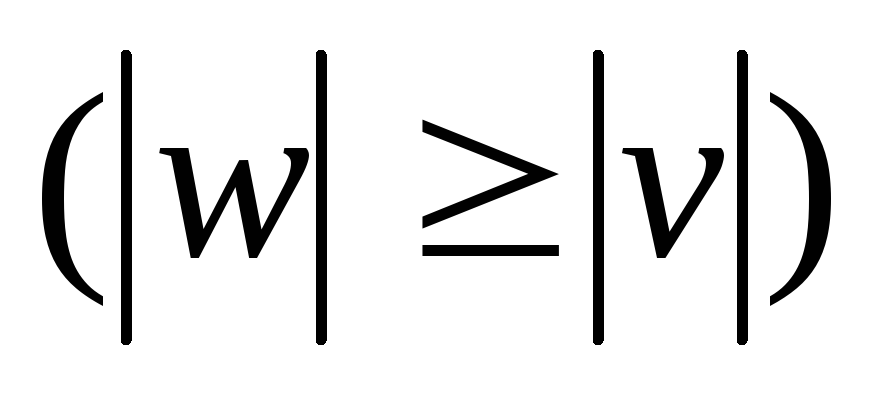контекстно-зависимой без ограничений (тип 0), если
,
.
Язык, порождаемый
грамматикой типа
,
называется языком типа
.
Таким образом язык
,
порождаемый приведенной выше грамматикой
,
является контекстно-свободным, а язык
-
контекстно-зависимым языком типа 1.
Рассмотрим в качестве примера еще две
грамматики, порождающие идентификаторы
языка программирования, состоящие из
первой буквы, за которой следует целое
число. Грамматика
является
праволинейной и содержит следующие
продукции:
Следующая грамматика определяет то же самое множество идентификаторов, но представляет собой контекстно-свободную грамматику с множеством продукций:
В эту грамматику
дополнительно включен нетерминальный
символ
для обозначения цифр. Язык, порождаемый
обоими грамматиками представляет собой
множество предложений
,
где
.
Определенные выше
четыре типа языков и грамматик называют
иерархией Хомского. В приведенном
определении контекстно-свободной
грамматики недопустимыми являются так
называемые
-
продукции, продукции вида
.
Однако многие авторы включают такие
продукции в число допустимых продукций
контекстно-свободных грамматик, а
контекстно-свободные грамматики без
-
продукций называют
-свободными
грамматиками[2]. Конечно при разработке
трансляторов более удобно использовать
именно такие грамматики без
-
продукций. Но и при наличии в грамматике
-
продукции ситуация не является
безнадежной, поскольку доказано, что
для любого контекстно-свободного языка
существует
-
свободная контекстно-свободная грамматика
,
такая, что
.
Построение такой грамматики несложно
[2].
С точки зрения приложений к языкам программирования наиболее подходящими являются контекстно-свободные грамматики. Это связано с тем, что с помощью этих грамматик удается достаточно полно описать синтаксис существующих языков программирования. С точки зрения трансляции наиболее важным вопросом, на который необходимо иметь ответ, является вопрос о наличии нескольких выводов из начального символа одного и того же предложения языка.
Для представления
вывода
,
где
обычно используется дерево вывода.
Вершины дерева помечены символами из
множества
.
Корнем дерева является вершина, помеченная
начальным символом
,
а листьями вершины с терминальными
символами. Все промежуточные вершины
дерева помечены нетерминалами множества
.
Рассмотрим
грамматику
,
которая описывает множество арифметических
выражений над переменными
и
.
Множество правил P включает в себя
следующие продукции:
Поскольку одна и
та же строка может получена в результате
нескольких выводов, их подразделяют на
два типа левосторонние и правосторонние.
Схема вывода предложения
называется левосторонней (правосторонней),
если подстановка очередного правила
осуществляется всегда на место самой
левой (правой) сентенциальной формы.
Два вывода строки
выглядят следующим образом
левосторонний
правосторонний
Построим дерево
для левостороннего вывода строки (рис.
1.5). Легко убедиться, что дерево для
правостороннего вывода будет точно
таким же. Контекстно-свободную грамматику,
в которой все возможные схемы выводов
строки
соответствуют одному и тому же дереву
вывода будем называть однозначной.
Примером неоднозначной грамматики
может служить грамматика
с продукциями
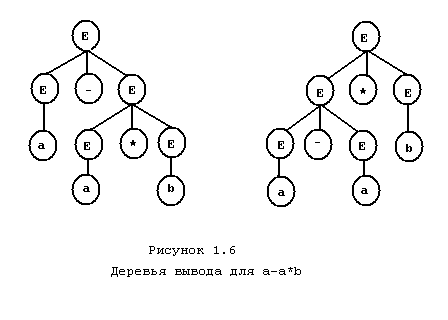
Для выражения
можно построить два разных дерева вывода
(рис. 1.6). В дальнейшем нас будут интересовать
в основном однозначные грамматики.
