Лекции / вар2 / Lecs3

Раздел 1. Формальные грамматики

Лекция 3.

Тема лекции. Основные типы контекстно-свободных грамматик. Методы разбора формальных языков.

3.1. Основные типы контекстно-свободных грамматик

Накладывая ограничения на правые части продукций контекстно-свободных (КС) грамматик можно выделить ряд их типов, которые нашли наиболее широкое практическое применение. Наиболее простой КС грамматикой является - грамматика [5]. Для того, чтобы КС грамматика была – грамматикой необходимо выполнение следующих двух условий:

• правая часть каждой продукции начинается терминальным символом,

• если две продукции имеют совпадающие левые части, то правые части этих продукций должны начинаться различными терминальными символами.

Примером - грамматики может служить грамматика , где множество содержит продукции

Рассмотрим еще одну грамматику [5], где содержит

Эта грамматика не является s - грамматикой из-за наличия продукции .

Для того, чтобы определить следующий тип более сложной КС грамматики, необходимо определить два множества: множество терминалов, следующих за данным нетерминалом, и множество выбора продукций. Первое множество обозначим через , второе - , где - продукция . Определим для КС грамматики с начальным символом , как множество терминальных символов, которые могут следовать непосредственно за нетерминалом в какой-либо сентенциальной форме, выводимой из . Другими словами , если и для каждого терминального символа существует вывод , где . Например, для приведенной выше грамматики .

Если продукция грамматики имеет вид , где , , то . Если продукция имеет вид , то. Теперь можно определить тип грамматики, пример которой приведен выше.

Контекстно-свободная грамматика называется - грамматикой, если выполняются два следующих условия:

• правая часть каждой продукции либо начинается с терминального символа, либо представляет собой ;

• множества выбора продукций с одной и той же левой частью не пересекаются.

Рассмотрим Множества выбора для грамматики .

Множества для продукций, содержащих в левой части символ , не пересекаются. Для второй пары продукций множества выбора будут выглядеть следующим образом.

Поскольку в правых частях продукций за символом может следовать , если на место в эти продукции поставить или , то окажется, что после символа могут следовать символы . Множества и не пересекаются. Оба условия для –грамматики выполняются. Поэтому можно сделать вывод что - –грамматика.

В рассмотренных простых КС грамматиках все правые части продукций представляли либо пустую строку, либо строку, в начале которой находился терминальный символ. Снимем эти ограничения и будем рассматривать грамматики, где правые части продукций начинаются и с терминальных и с нетерминальных символов. В связи с этим расширим понятие множества выбора, назовем его множеством направляющих символов и обозначим DR(p), где .

Множество 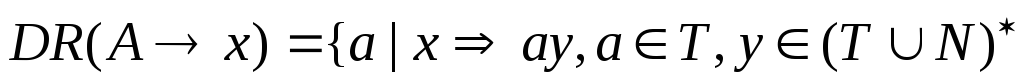или . Теперь мы готовы определить следующую грамматику. КС грамматика называется LL(1)-грамматикой тогда и только тогда, когда множества направляющих символов для правил с одинаковой левой частью не пересекаются. Приведем пример LL(1) грамматики , которая имеет следующие продукции

Приведённая выше грамматика не является –грамматикой, так как есть продукции, правая часть которых начинается не с терминального символа. Для тренировки найдём множества направляющих символов для всех правил грамматики .

Поскольку и .

, поскольку . Множества не пересекаются.

поскольку или . Множества не пересекаются.

Эти множества также не пересекаются. В целом получилось, что все условия для LL(1)-грамматики выполняются, то есть – LL(1)-грамматика.

Приведенный тип грамматики является частным случаем LL(k) грамматик при . Дадим определение LL(k) грамматики. Для этого введем функцию FIRST

, где

, если

, если

Тогда КС грамматика называется LL(k)-грамматикой для некоторого фиксированного k, если из существования двух левых выводов

,

для которых , вытекает, что [1]. Примером LL(2) грамматики может служить грамматика с продукциями

Действительно, рассмотрим два левосторонних вывода

Мы видим, что . Однако . Поэтому грамматика не является LL(1)-грамматикой.

Найдём подтверждения, что LL(2)-грамматика. Рассмотрим следующие левосторонние выводы:

Строка может быть пустой при выводе , или при выводе , или при выводе . Таким образом, видно, что различно для каждого правила, то есть по двум символам можно всегда выбрать только одно правило. По символам правило , по правило , по правило .

Аналогично рассмотрим правила с нетерминалом в левой части

(правило )

(правило )

Для второго правила могут быть следующие выводы.

Таким образом, правило можно выбрать однозначно по текущим символам , а правило по текущим символам , причём по символу , если последний в строке. Таким образом условия LL(2)-грамматики выполняются для .

Важным свойством LL(k) грамматик является то, что они однозначны [2]. Таким образом, если удается показать, что исследуемая грамматика - LL(k)- грамматика, то тем самым удается подтвердить ее однозначность. В основу приведенных выше определений LL(k) - грамматик положен левосторонний вывод. Однако более широкий класс языков определяется LR-грамматиками, которые опираются на правосторонний вывод.

Контекстно-свободная грамматика называется LR(0) грамматикой, если из условий:

• ни одна из ее продукций не содержит в правой части исходного символа

• существуют две правосторонние схемы вывода

,

,

где , вытекает, что [2].

Введем множество , где - правосторонняя схема вывода, . Используя это множество можно показать [2], что КС грамматика является LR(0)- грамматикой, если

1. ни одна из ее продукций ни содержит начального символа в своей правой части,

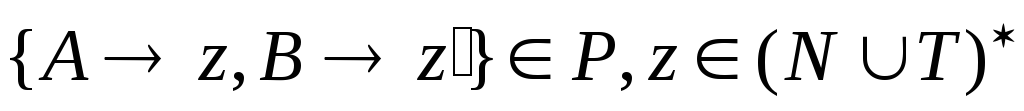2. из и , где и 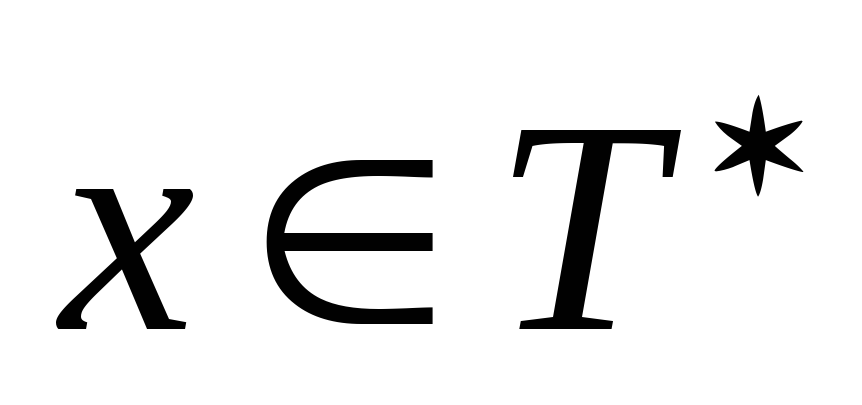, вытекает, что .

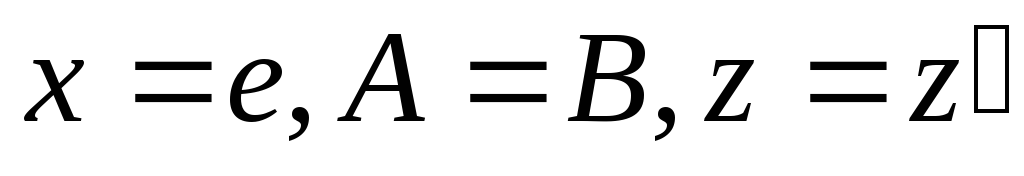Дальнейшим обобщением LR- грамматик являются LR(k)- грамматики. На основе грамматики введем пополненную грамматику , где . Тогда грамматику G будем называть LR(k)-грамматикой для , если из условий:

,

,

следует ( т.е. ).

Примером LR(2)- грамматики может служить грамматика ,

имеющая следующие продукции [6]

Важным свойством LR(k)- грамматик является то, что любой LR(k) язык является также LR(1) языком и даже LR(0) языком, если допустить, что за каждым его предложением следует знак окончания.

3.2. Методы разбора формальных языков

В предыдущем разделе был рассмотрен метод описания языков с помощью формальных грамматик. Второй основной метод описания языка базируется на использовании распознавателей. Распознаватель можно представить в виде алгоритма, определяющего некоторое множество предложений языка.

Распознаватель состоит из трех частей (рис. 1.7) входной ленты, управляющего устройства с конечной памятью и вспомогательной или рабочей памяти [1]. Потенциально неограниченная в обе стороны входная лента представляет собой последовательность ячеек, содержащих точно по одному символу некоторого конечного алфавита T. Крайние правую и левую ячейки входной ленты можно пометить специальными символами - концевыми маркерами.

Считывающая головка в каждый момент времени указывает на одну ячейку входной ленты. За один шаг работы распознавателя она может сдвинуться на одну ячейку вправо или влево по входной ленте. Отметим, что головка только "читает" текущий символ на ленте, не изменяя его. В дальнейшем основное внимание мы будем уделять односторонним распознавателям, считывающая головка которых двигается только слева направо.

Вспомогательная память предназначена для хранения дополнительной информации, непосредственно влияющей на процесс работы распознавателя. Как правило, она имеет сложную структуру и построена из символов некоторого алфавита (обозначим его M). В частности память можно представить в виде структуры, состоящей из строк множества . Для работы с памятью используются две функции: функция доступа к памяти и функция преобразования памяти. Первую функцию можно представить в виде отношения . Функция f каждому текущему состоянию памяти - структуре строк из ставит в соответствие один элемент структуры - строку из . Вторая функция может иметь вид , она преобразует структуру памяти в зависимости от помещаемой в память информации - строки из . В дальнейшем мы будем рассматривать распознаватели, у которых вспомогательная память реализована в виде магазина.

Управляющее устройство содержит конечное множество состояний (обозначим его через Q), среди которых выделены одно начальное состояние и подмножество конечных состояний. Управляющее устройство осуществляет перевод распознавателя из одной конфигурации в другую. Конфигурация представляет собой тройку , где - текущее состояние управляющего устройства, - неиспользованная часть входной ленты вместе с текущим символом , на который указывает считывающая головка, - текущее содержимое вспомогательной памяти. В начальной конфигурации управляющее устройство находится в начальном состоянии, считывающая головка указывает на самый левый символ строки во входной ленте, вспомогательная память имеет начальное содержимое. В заключительной конфигурации управляющее устройство находится в одном из конечных состояний, считывающая головка указывает на ячейку, следующую за последним символом строки на входной ленте, вспомогательная память имеет некоторую заранее оговоренную структуру.

Распознаватель работает по отдельным шагам, переходя из одной конфигурации в другую. На каждом шаге выполняется одна и та же последовательность действий:

• считывающая головка сдвигается на одну ячейку вправо,

• в зависимости от считанного символа на входной ленте и состояния памяти модифицируется ее содержимое,

• изменяется состояние управляющего устройства в соответствии с текущим состоянием входной ленты, текущим состоянием управляющего устройства, содержимым вспомогательной памяти.

Если на каждом шаге работы распознавателя существует не более одной допустимой конфигурации, куда он может перейти, распознаватель называют детерминированным, если несколько допустимых конфигураций - недетерминированным. Говорят, что распознаватель допускает строку, если, поместив ее на входную ленту, он переходит из начальной конфигурации в одну из заключительных. Множество допускаемых строк составляют язык, определяемый распознавателем.

В процессе своей работы распознаватель может устанавливать синтаксическую структуру предложения, заданную деревом разбора. Процесс построения дерева разбора исходного предложения называют разбором или

синтаксическим анализом. Можно пронумеровать продукции в грамматике и представлять разбор конкретного предложения в виде последовательности номеров продукций, применяемых при выводе этого предложения. Например, пронумеруем правила грамматики, приведенной в разделе 1.2.2

(1)

(2)

(3)

(4)

(5)

(6)

(7)

Тогда разбор строки можно представить в виде последовательностей 2,6,3,6,7 или 3,2,6,6,7 (рис. 1.6). Левым разбором строки x называется последовательность продукций, примененных при левом выводе строки x из начального символа S. В рассмотренном примере приведены два левых разбора. Правым разбором строки x называется обращение последовательности продукций, примененных при правом выводе строки x из начального символа S. Пример правого разбора строки выглядит следующим образом {6,6,7,3,2}.

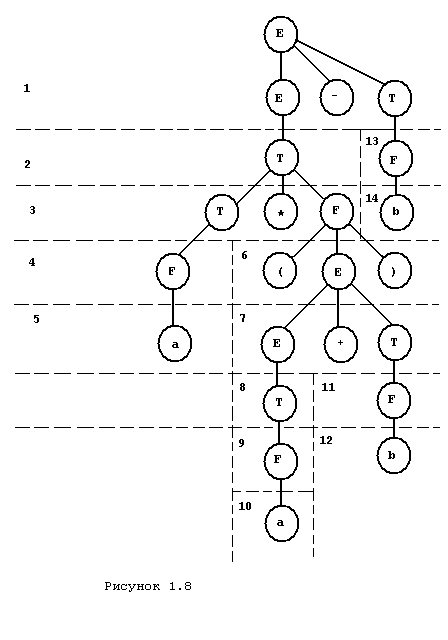
Большинство методов разбора сводится к двум основным вариантам сверху вниз и снизу вверх. Построение дерева методом сверху вниз или при нисходящем анализе начинается с корня дерева. Каждая внутренняя вершина раскрывается в том случае, если известны и построены все ее вершины предшественники. Решение о том, какую продукцию необходимо использовать для раскрытия внутренней вершины принимается на основе текущих символов на входной ленте и во вспомогательной памяти. Вариант построения дерева (рис. 1.5) методом сверху вниз показан на рисунке 1.8.

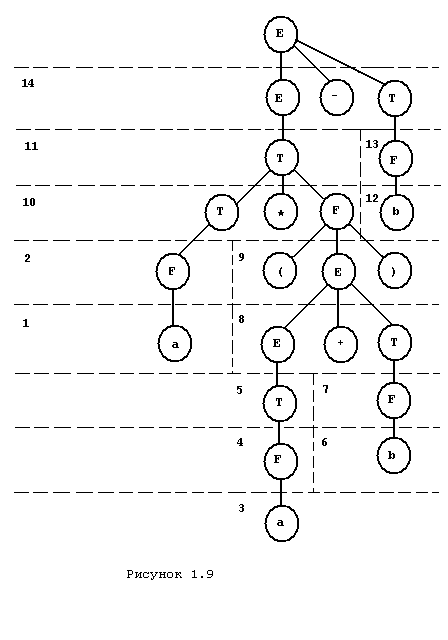
При использовании метода снизу вверх заполнение начинается с листьев дерева. Следующая по порядку вершина дерева строится в том случае, если все ее вершины преемники принадлежат построенной части дерева. Дерево, изображенное на рисунке 1.5 может быть построено снизу вверх, как показано на рис. 1.9. Приведенный метод разбора также называют восходящим методом. В последнее время появился ряд методов, которые впрямую не используют ни одну из предложенных двух стратегий разбора. Один из таких методов называют методом горизонтального разбора. Он характеризуется тем, что некоторая вершина рассматривается в том случае, если она висячая вершина и соответствует текущему символу входной ленты или она является предшественником рассматриваемой вершины [7].

Вариант построения дерева горизонтального разбора представлен на рис. 1.10.

11