1.3.2. Магазинные автоматы
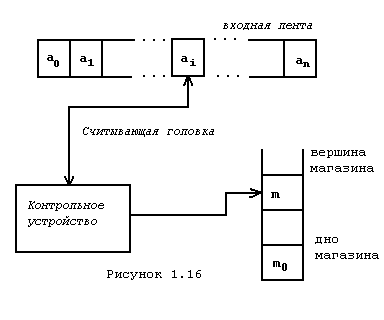
Если конечные автоматы дают возможность построить распознаватель для языка, порожденного праволинейной грамматикой, следующий вид автоматов нацелен на распознавание контекстно-свободных языков. С повышением сложности рассматриваемого языка повышается и сложность автомата. Магазинный автомат - это односторонний в общем случае недетерминированный распознаватель, у которого в качестве вспомогательной памяти используется магазин (рис.1.16). Магазин можно представить в виде строки символов, правый символ которой называют дном магазина, а левый вершиной магазина. Из строки можно считать в определенный момент времени только символ вершины магазина. Причем при считывании символа он удаляется из магазина и вершиной магазина становится следующий (правый) по порядку символ. При записи символов в магазин они помещается слева от вершины магазина и в дальнейшем последний из них рассматривается как новая вершина магазина.
Магазинный автомат или автомат с магазинной памятью (МП - автомат) - это семерка
,
где
Q - конечное множество состояний;
T - конечный входной алфавит;
M - конечный алфавит магазинных символов (стековый алфавит);
- начальное состояние автомата;
- начальный символ магазина;
- конечное множество заключительных
состояний;
t - функция переходов
отображает тройки, образованные
состоянием, текущим входным символом
на входной ленте или пустым символом
и вершиной магазина в множество
всех подмножеств
.
В начале работы на входной ленте записано
исходное предложение, ограниченное с
двух сторон концевыми маркерами,
считывающая головка установлена на
первый символ предложения, магазин пуст
и содержит начальный символ магазина,
магазинный автомат находится в начальном
состоянии. В процессе функционирования
строка на входной ленте просматривается
слева направо без возвратов. На каждом
шаге автомат переходит из одной
конфигурации в следующую.
Под конфигурацией магазинного автомата понимают тройку
-
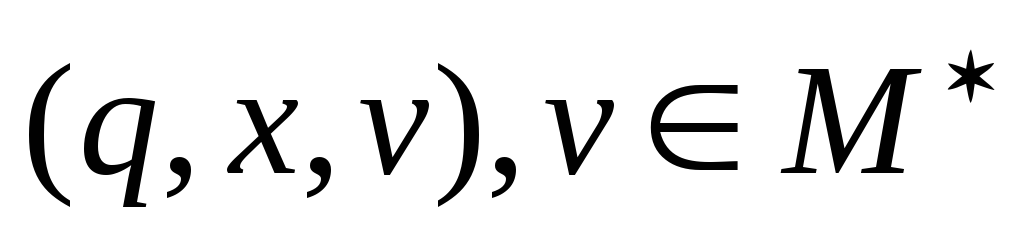- содержимое магазина,
-
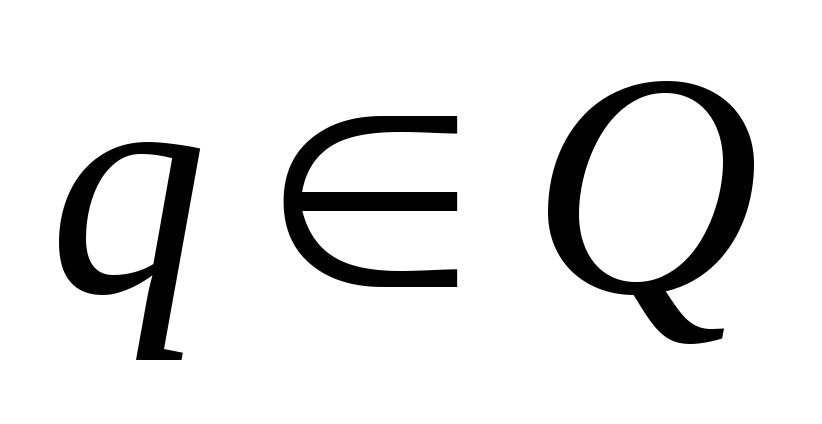- текущее состояние магазинного автомата,
-
- часть исходной строки на входной
ленте,
начинающаяся с текущего символа (на
который указывает считывающая головка)
и кончающаяся последним символом строки.
Конфигурацию можно также записать в
виде
или
,
или
,
где
- символ на вершине магазина. Начальная
конфигурация в этом случае записывается
в виде
,
заключительная конфигурация -
,
где
и
.
Для записи перехода автомата из одной
конфигурации в другую применяется
бинарное отношение ├, определенное на
конфигурациях автомата. Будем писать
├
,
где
если пара
и
.
Символ
считается допущенным, если автомат
читает его из входной строки и переходит
из конфигурации
в конфигурацию
.
При этом читающая головка перемещается
на один символ вправо и символ m в
вершине магазина заменяется строкой
магазинных символов b. Если
,
то происходит сокращение содержимого
магазина на символ m, при этом в
вершине магазина будет содержаться
следующий магазинный символ.
Строка символов
,
где
допускается магазинным автоматом, если
существует последовательность
конфигураций такая, что
├
,
где
.
Поскольку разработчиков компиляторов
мало интересуют пустые символы в строках,
уберем их из определения допускаемой
строки. Тогда строка
,
где
,
допускается автоматом A, если
существует аналогичная строка, допускаемая
автоматом A, в которой
.
Последовательность конфигураций,
которые принимает магазинный автомат
при распознавании строки x обозначается
├
,
где
.
Если конечное состояние магазина
совпадает с начальным
,
говорят, что строка
допускается автоматом A с опустошенным
магазином [4].
├
Если автомат имеет пустой начальный
символ магазина
,
то говорят, что он допускает строку x
с пустым магазином.
├
Язык T(A), допускаемый магазинным автоматом, представляет собой множество строк, определяемых формуло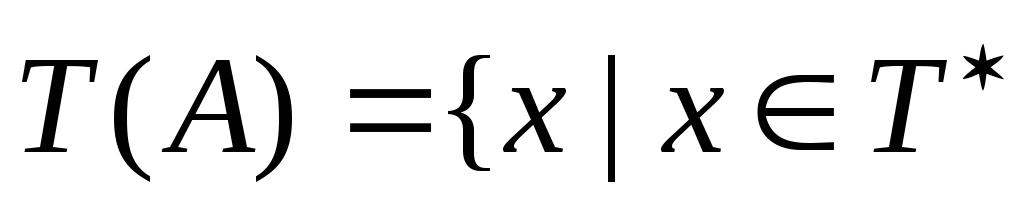й
и
├
Рассмотренный магазинный автомат
позволяет на каждом шаге, либо удалить
символ в вершине магазина, либо заменить
его строкой магазинных символов конечной
длины. Это ограничение снято при
определении расширенного магазинного
автомата [1], который позволяет заменять
строки конечной длины , прилегающие к
вершине магазина. Данный магазинный
автомат является недетерминированным,
поскольку
или
имеют множество значений (которое
может содержать и более одного элемента)
и в общем не существует правила для
выбора единственного значения из
множества. Множество может быть и пустым,
тогда автомат не может допускать
следующие входные символы.
Описанные выше магазинные автоматы
могут применяться в качестве
недетерминированных распознавателей
контекстно-свободных языков.
Доказано [1,4], что каждой КС грамматике
соответствует магазинный автомат A,
такой, что
.
Недетерминированный магазинный
автомат в виде нисходящего распознавателя
строится следующим образом. Определим
множества, описывающие автомат A.
- множество состояний;
T - входной алфавит состоит из терминальных символов;
- алфавит магазинных символов содержит
терминальные и нетерминальные символы;
- начальное состояние;
- начальный символ магазина;
- множество конечных состояний.
Функция перехода t определяется следующим образом:
-
если множество продукций P содержит правило
,
то
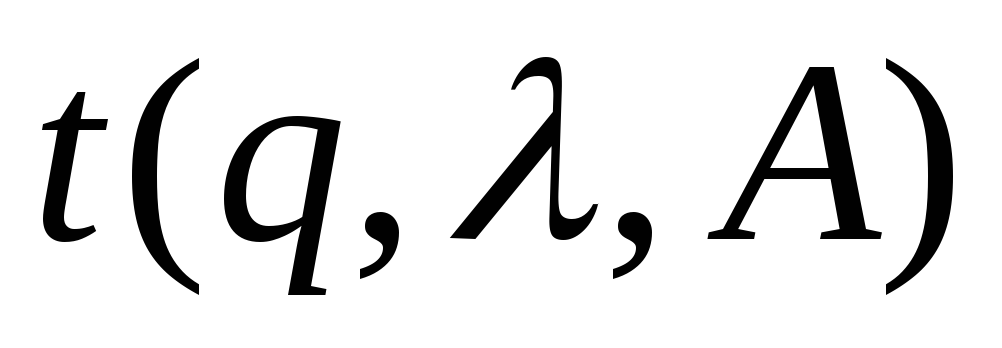содержит
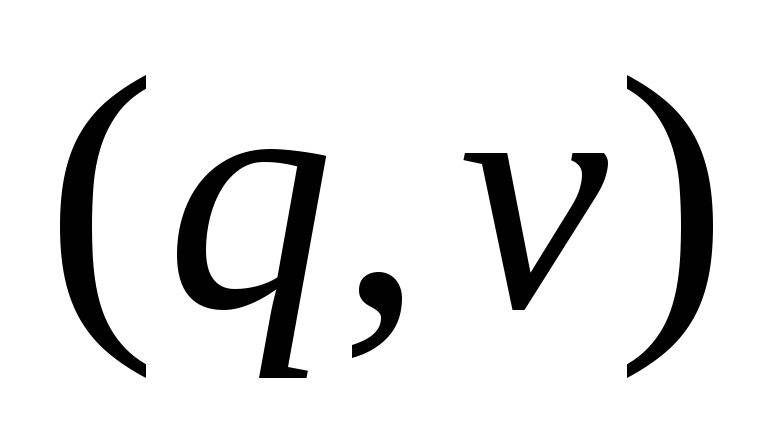для всех продукций с нетерминалом A
в левой части;
-
для
.
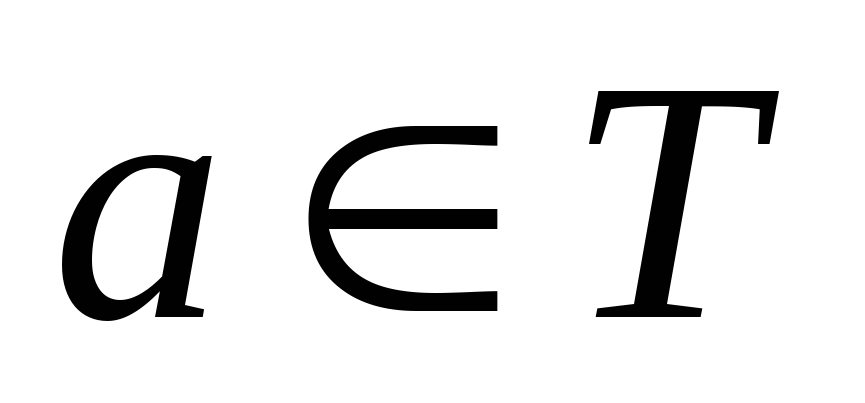Построим магазинный автомат для
приведенной в разделе 1.2.2 грамматики
с продукциями
Автомат будет представлять семерку
,
функция перехода которого имеет вид:
для всех
При распознавании строки
,
дерево вывода которой представлено на
рис. 1.5 автомат может пройти по следующей
последовательности конфигураций.
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
Изобразим в виде графа состояний
недетерминированный автомат, моделирующий
при распознавании левые выводы строк.
Множество V построим таким образом,
что каждой вершине соответствует
нетерминальный символ. Дополним это
множество специальной вершиной для
допуска входных символов строки,
обозначим ее g ( эта
вершина является конечной). Тогда
множество
.
Две вершины, помеченные нетерминальными
символами
,
соединяются ребром
,
если значение функции перехода
не пусто и
.
При переходе по такому ребру графа
автомат выполняет шаг
├
.
В случае
для шага автомата
├
на графе вводится ребро
.
Аналогично при
вводится ребро
для выполнения шага
├
.
Для значений функции
,
где
вводится ребро
для шага
├
.
Все вершины графа мы соединили ребрами
в соответствии с функцией перехода.
Однако вершина g не имеет выходящих
ребер. Не дополняя функцию перехода,
соединим вершину g со всеми остальными
вершинами. При переходе по такому ребру
конфигурация автомата не изменяется,
т.е. можно записать
├
для ребра
.
Смену конфигураций при проходе по ребру
будем записывать на нем в виде тройки
,
где a – допускаемый символ входной
строки, b - удаляемый из магазина
символ (для расширенного автомата строка
символов), c - помещаемая в магазин
строка символов. Разметка ребер для
приведенных шагов автомата будет
выглядеть следующим образом.
├
,A,Bw
или , A,Bw
├
,A,
,A,
├
,A,aw ,A,aw
├
a,a,
├
,A,A ,A,A
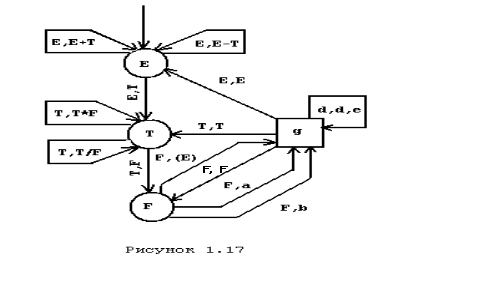
Для рассмотренного выше магазинного автомата граф состояний представлен на рис. 1.17.
Как отмечалось выше можно построить
расширенный МП автомат, моделирующий
правый вывод строки
.
Такой автомат строится следующим образом
[1]:
- множество состояний;
T - входной алфавит;
- алфавит магазинных символов;
q - начальное состояние автомата;
# - начальный символ магазина;
{r} - множество заключительных состояний.
Функция перехода t:
содержит
,
если в грамматике существует продукция
;
для всех
;
.
Для задания автомата определим граф
,
множество вершин которого
.
Для функции
в графе задается ребро
,
при переходе по которому выполняется
шаг
├
,
.
Здесь и далее при записи конфигураций
автомата строка в магазине записывается
в обратном порядке, т.е. дно магазина
расположено на левом крае строки, а
вершина на правом. Если
,
то задается ребро
с шагом автомата
├
.
Аналогично поступаем, если
.
Задаем ребро
с шагом
├
.
Перенос символов с входной ленты в
магазин будет производиться на ребре
с шагом
├
в соответствии с функцией
.
Для допуска начального символа грамматики
S вводится ребро
с шагом
├
для функции
.
Поскольку после каждой замены подстроки
в магазине на нетерминальный символ
возможен перенос символов с входной
ленты в магазин вводим ребра
,
не изменяющие конфигурацию автомата.
Построим автомат для рассмотренной
выше грамматики. Он определяется семеркой
.
Функция перехода автомата будет
следующей.
для всех
Граф состояний для данного автомата приведен на рис. 1.18.
Строка
может распознаваться автоматом в
следующем порядке.
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
├
Мы рассмотрели два типа магазинных автоматов. Между ними и контекстно-свободными грамматиками существует полное соответствие. Однако эти автоматы недетерминированные и использовать их для построения трансляторов с рекурсивных языков (Паскаль, Ада и др.) сложно. Недетерминированный разбор предусматривает возвраты, а в рекурсивных языках возвращаться назад приходится не только в текущей строке, но и во всей программе. При трансляции параллельно с синтаксическим анализом выполняется ряд семантических действий над программой. Возврат может вызвать отмену выполненных действий, что затруднительно, а иногда просто невозможно.
Детерминированность автомата, возможность его построения зависит от типа используемой контекстно-свободной грамматики. В теории выделены два типа грамматик LL(k) и LR(k), для которых можно построить детерминированные магазинные автоматы, работающие по принципам как сверху-вниз, так и снизу-вверх. Ограничения, которые наложены на КС-грамматики данных классов, рассматривались выше. Известны методы построения детерминированных автоматов LL(k) и LR(k) - грамматик. Они достаточно подробно рассмотрены в литературе [1,6,7] и останавливаться на них специально мы не будем. Однако эти грамматики и способ построения детерминированных автоматов будут внимательно изучены в свете предлагаемого в книге подхода.