
1396_49892_reshebnik / Задание / 8 Векторный анализ
.doc§ 8.1. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
-
Скалярное поле. Производная по направлению.
-
Градиент, его свойства. Инвариантное определение градиента.
-
Векторное поле. Поток векторного поля через поверхность, его физический смысл.
-
Формула Остроградского.
-
Дивергенция векторного поля, ее физический смысл. Инвариантное определение дивергенции. Свойства дивергенции.
-
Соленоидальное поле, его основные свойства.
-
Линейный интеграл в векторном поле, его свойства и физический смысл.
-
Циркуляция векторного поля, ее гидродинамический смысл.
-
Формула Стокса.
-
Ротор векторного поля, его свойства. Инвариантное определение ротора.
-
Условия независимости линейного интеграла от формы пути интегрирования.
-
Потенциальное поле. Условия потенциальности.
§ 8.2. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
-
Найти производную скалярного поля
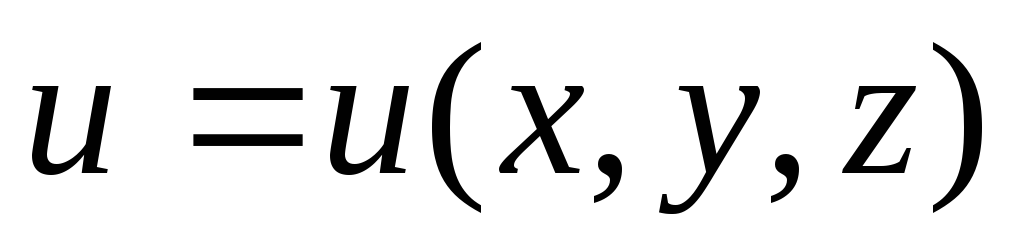 по
направлению градиента скалярного поля
по
направлению градиента скалярного поля

-
Найти градиент скалярного поля
 ,
где
,
где
 —
постоянный вектор, а
—
постоянный вектор, а
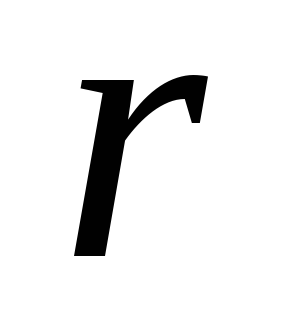 —
радиус-вектор. Каковы поверхности
уровня
этого поля и как они расположены по
отношению к вектору
—
радиус-вектор. Каковы поверхности
уровня
этого поля и как они расположены по
отношению к вектору
 ?
? -
Доказать, что если 5 — замкнутая кусочно-гладкая поверхность и
 —
ненулевой постоянный вектор, то
—
ненулевой постоянный вектор, то
![]()
где
![]() —вектор,
нормальный к поверхности
—вектор,
нормальный к поверхности
![]() .
.
-
Доказать формулу
![]()
где
![]() ;
;![]() —
поверхность, ограничивающая объем
—
поверхность, ограничивающая объем
![]() ;
;
![]() —
орт внешней нормали к поверхности
—
орт внешней нормали к поверхности
![]() .
Установить условия применимости формулы.
.
Установить условия применимости формулы.
-
Доказать, что если функция
 удовлетворяет
уравнению
Лапласа
удовлетворяет
уравнению
Лапласа
![]() то
то
![]()
где
![]() — производная по направлению нормали
к кусочно-гладкой замкнутой поверхности
— производная по направлению нормали
к кусочно-гладкой замкнутой поверхности
![]() .
.
-
Доказать, что если функция
 является
многочленом второй степени и
является
многочленом второй степени и
 —
кусочно-гладкая замкнутая поверхность,
то интеграл
—
кусочно-гладкая замкнутая поверхность,
то интеграл
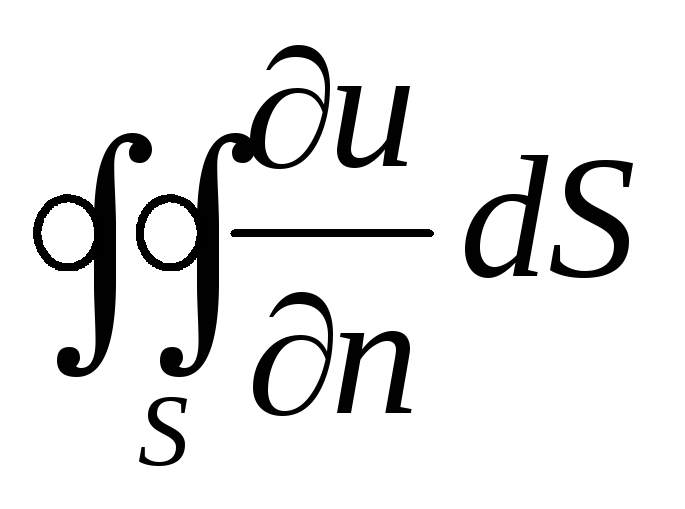 пропорционален объему, ограниченному
поверхностью
пропорционален объему, ограниченному
поверхностью
 .
. -
Пусть
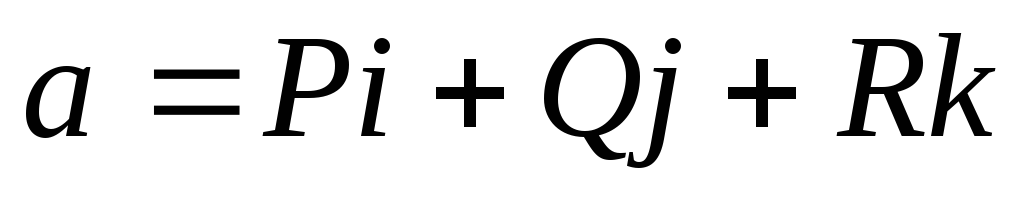 ,
где
,
где
 —
линейные
функции от
—
линейные
функции от
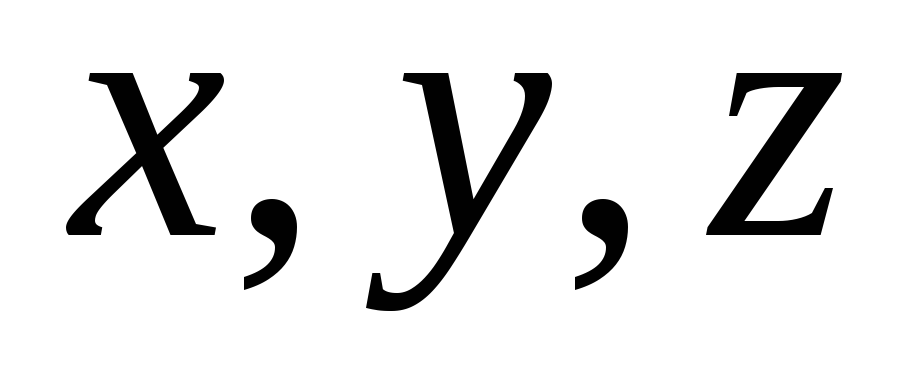 ,
и
пусть
,
и
пусть
 —
замкнутая кусочно-гладкая кривая,
расположенная в некоторой плоскости.
Доказать, что если циркуляция
—
замкнутая кусочно-гладкая кривая,
расположенная в некоторой плоскости.
Доказать, что если циркуляция
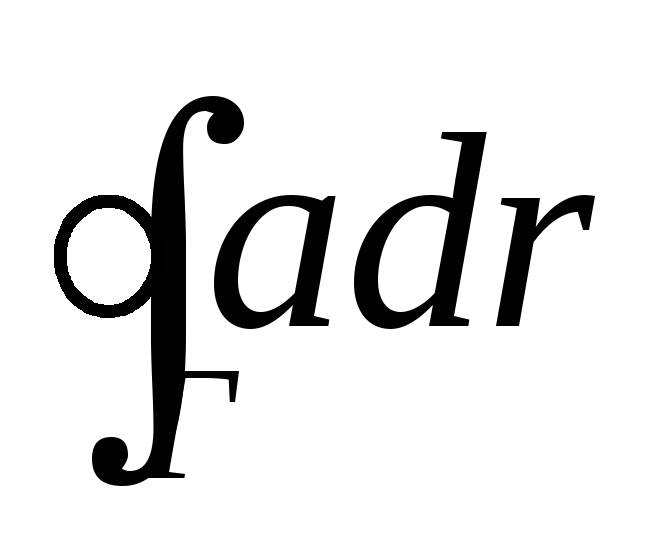 отлична от нуля,
то
она пропорциональна площади фигуры,
ограниченной контуром
отлична от нуля,
то
она пропорциональна площади фигуры,
ограниченной контуром
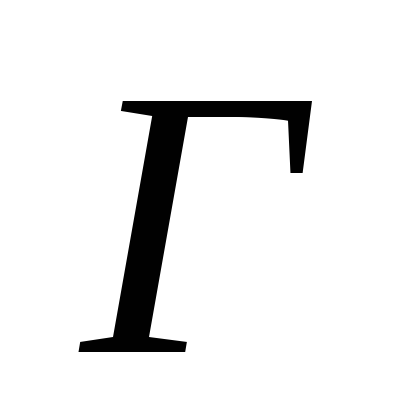 .
. -
Твердое тело вращается с постоянной угловой скоростью вокруг неподвижной оси, проходящей через начало координат. Вектор угловой скорости
 .
Определить ротор и дивергенцию поля
линейных скоростей
.
Определить ротор и дивергенцию поля
линейных скоростей
 точек тела (здесь
точек тела (здесь
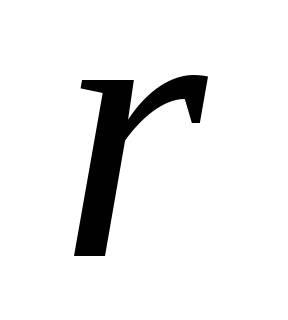 —
радиус-вектор).
—
радиус-вектор).
§ 8.3. РАСЧЕТНЫЕ ЗАДАНИЯ
Задача
1. Найти
производную скалярного поля
![]() в
точке
в
точке
![]() по направлению проходящей через эту
точку нормали к поверхности
по направлению проходящей через эту
точку нормали к поверхности
![]() ,
образующей острый угол с положительным
направлением оси
,
образующей острый угол с положительным
направлением оси
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
Найти
производную скалярного поля
![]() в
точке
в
точке
![]() по
направлению вектора
по
направлению вектора
![]() .
.
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача
2. Найти
угол между градиентами скалярных полей
![]() и
и
![]() в
точке
в
точке
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача
3.
Найти векторные линии в векторном поле
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача
4. Найти
поток векторного поля
![]() через
часть поверхности
через
часть поверхности
![]() ,
вырезаемую плоскостями
,
вырезаемую плоскостями
![]() (нормаль
внешняя к замкнутой поверхности,
образуемой данными поверхностями).
(нормаль
внешняя к замкнутой поверхности,
образуемой данными поверхностями).
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
Найти
поток векторного поля
![]() через
поверхности
через
поверхности
![]() ,
вырезаемую плоскостью
,
вырезаемую плоскостью
![]() (нормаль
внешняя к замкнутой поверхности,
образуемой данными поверхностями).
(нормаль
внешняя к замкнутой поверхности,
образуемой данными поверхностями).
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 5. Найти поток векторного
поля a через часть плоскости
![]() ,
расположенную в первом октанте (нормаль
образует острый угол с осью
,
расположенную в первом октанте (нормаль
образует острый угол с осью
![]() .
.
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 6. Найти поток векторного
поля
![]() через
часть плоскости
через
часть плоскости
![]() ,
расположенную в 1 октанте (нормаль
образует острый угол с осью
,
расположенную в 1 октанте (нормаль
образует острый угол с осью
![]()
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26.
![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]()
31.
![]()
Задача 7. Найти поток векторного
поля
![]() через
замкнутую поверхность
через
замкнутую поверхность
![]() (нормаль
внешняя).
(нормаль
внешняя).
1.
![]()
2.
![]()
3.
![]()
4.
![]()
5.
![]()
6.
![]()
7.
![]()
8.
![]()
9.
![]()
10.
![]()
11.
![]()
12.
![]()
13.
![]()
14.
![]()
15.
![]()
16.
![]()
17.
![]()
18.
![]()
19.
![]()
20.
![]()
21.
![]()
22.
![]()
23.
![]()
24.
![]()
25.
![]()
26![]()
27.
![]()
28.
![]()
29.
![]()
30.
![]() .
.
31.
![]()
Задача 8. Найти поток векторного
поля
![]() через
замкнутую поверхность
через
замкнутую поверхность
![]() (нормаль
внешняя).
(нормаль
внешняя).
1.
![]()

2.
![]()
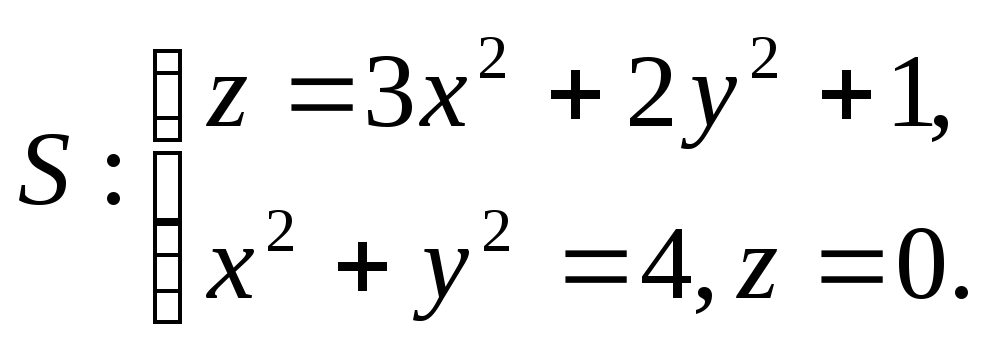
3.
![]()

4.
![]()

5.
![]()
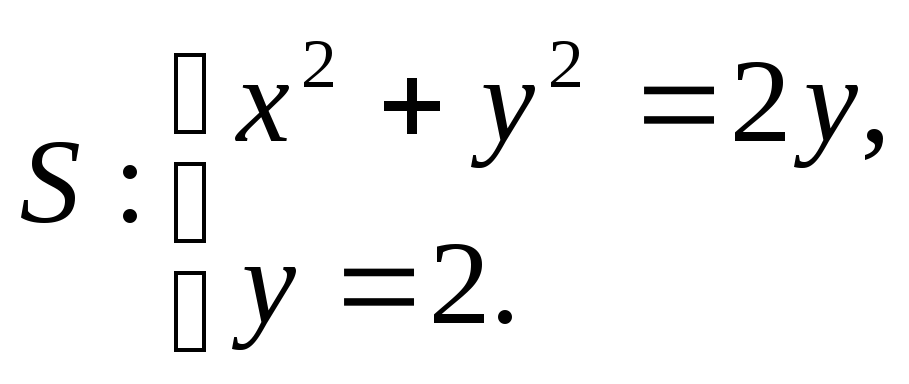
6.
![]()
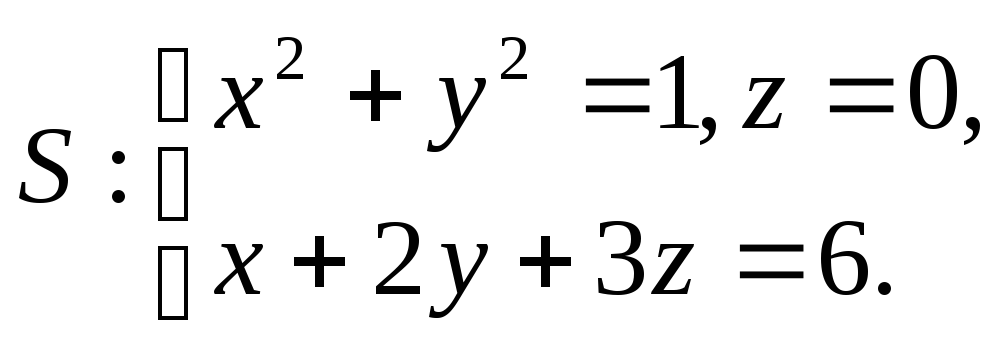
7.
![]()
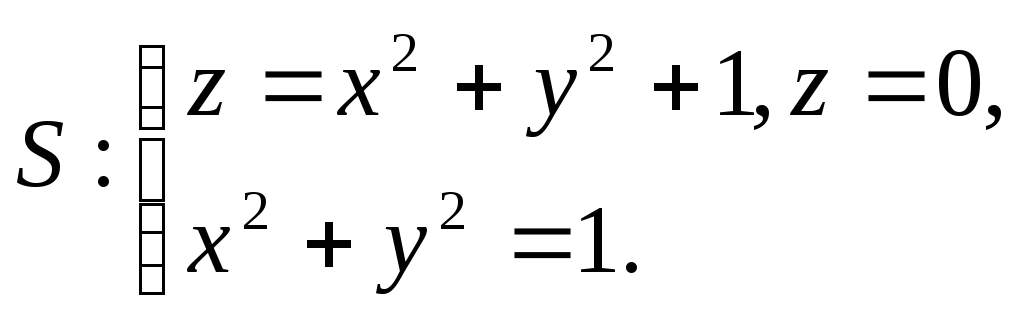
8.
![]()

9.
![]()

10.
![]()

11.
![]()
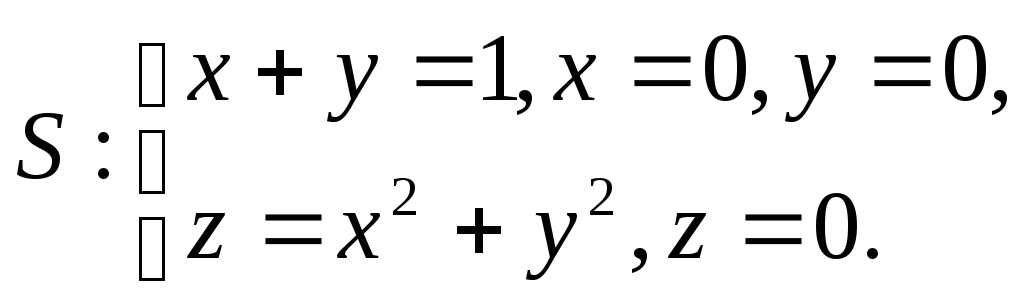
12.
![]()

13.
![]()
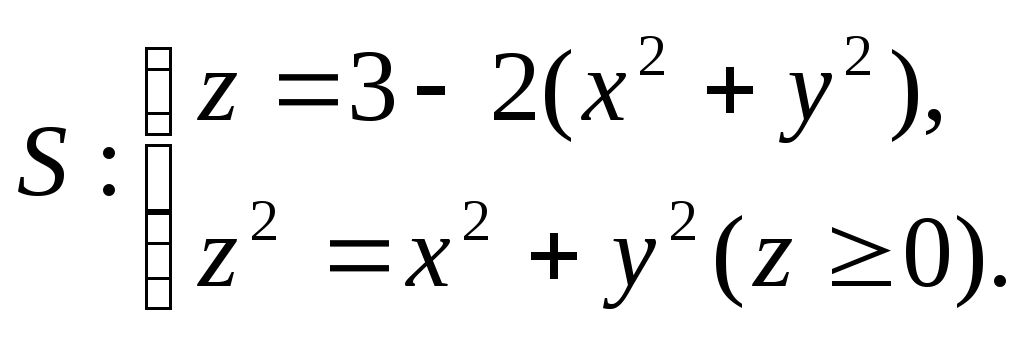
14.
![]()

15.
![]()

16.
![]()

17.
![]()
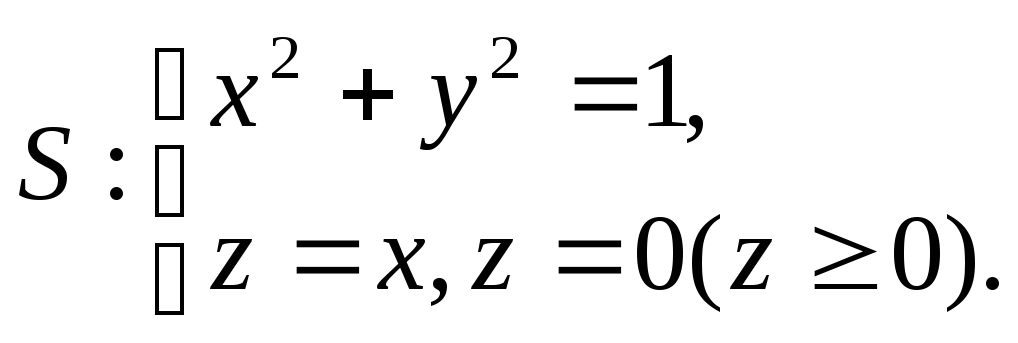
18.
![]()
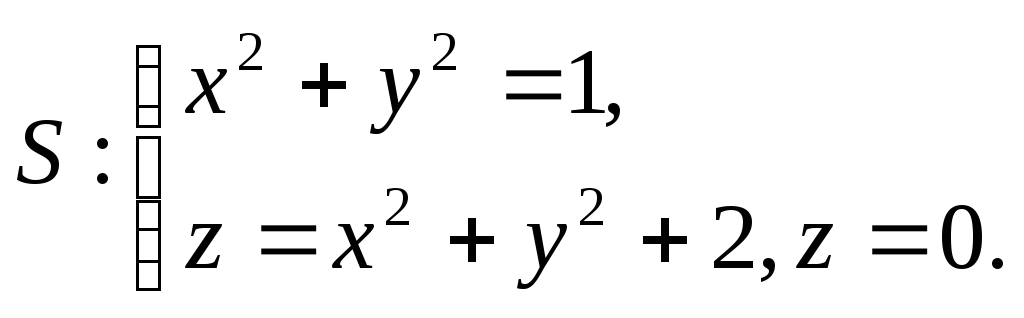
19.
![]()
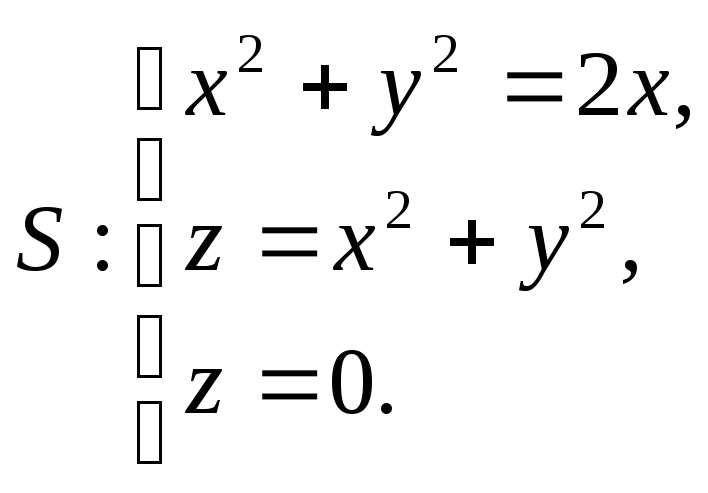
20.
![]()

21.
![]()
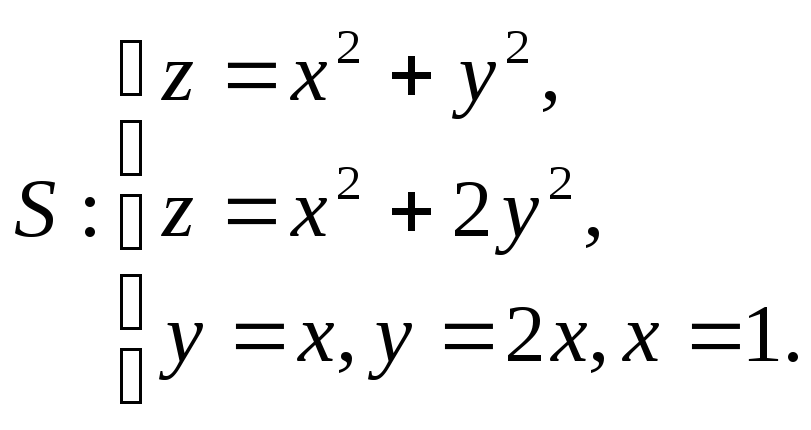
22.
![]()
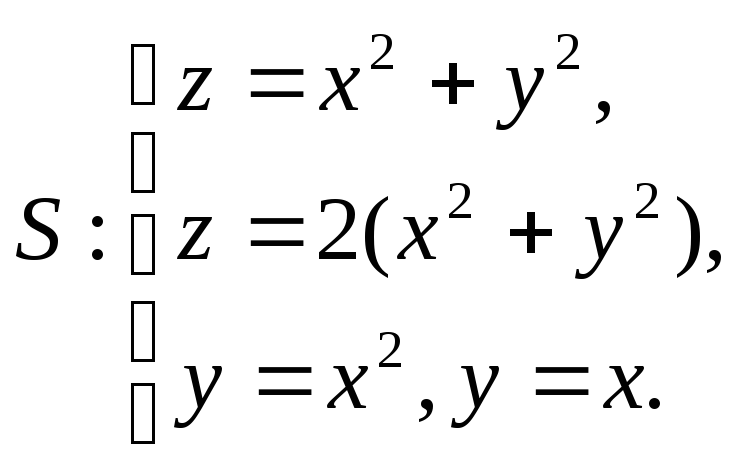
23.![]()
