1396_49892_reshebnik / Задание / 9 Аналитическая геометрия
.docПри необходимости более детального просмотра увеличьте масштаб документа!
www.otlichka.ru
§ 9.1. ТЕОРЕТИЧЕСКИЕ ВОПРОСЫ
-
Векторы. Линейные операции над векторами.
-
Скалярное произведение, его свойства. Длина вектора. Угол между двумя векторами.
-
Определители, их свойства.
-
Векторное произведение. Свойства. Геометрический смысл.
-
Смешанное произведение, его свойства. Геометрический смысл. Необходимое и достаточное условие компланарности трех векторов.
-
Плоскость. Уравнение плоскости.
-
Расстояние от точки до плоскости.
-
Уравнения прямой в пространстве. Нахождение точки пересечения прямой и плоскости.
§ 9.2. ТЕОРЕТИЧЕСКИЕ УПРАЖНЕНИЯ
-
Пусть векторы
и
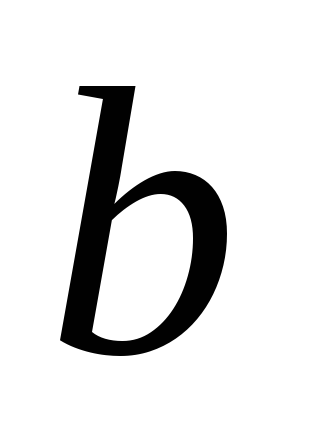не коллинеарны и
Найти
и
и доказать коллинеарность векторов
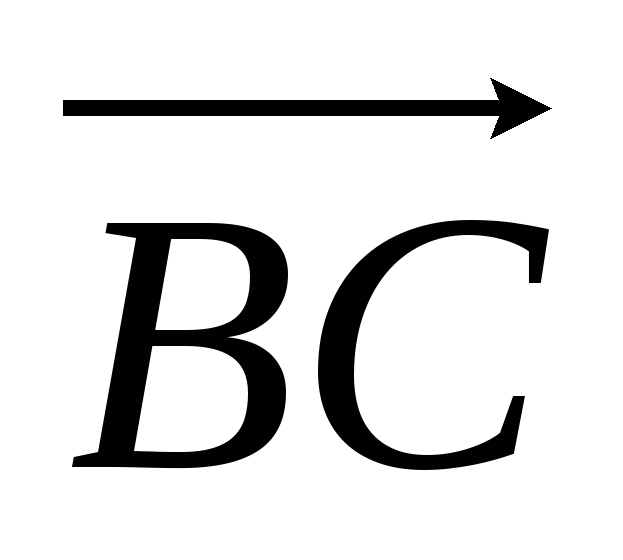и
. -
Разложить вектор
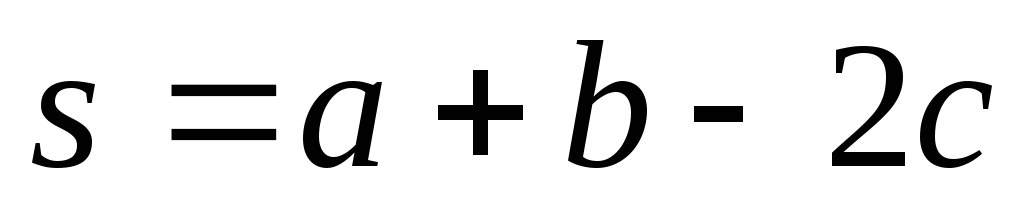по трем некомпланарным векторам
.
-
Найти угол между единичными векторам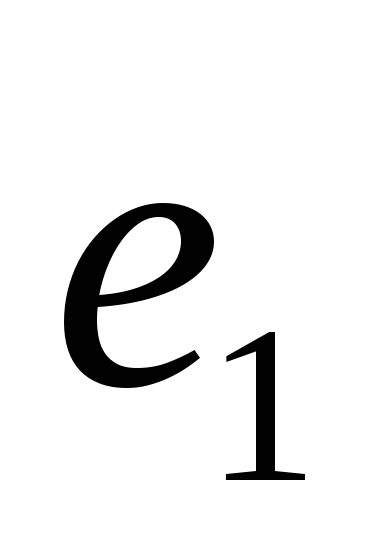и
и
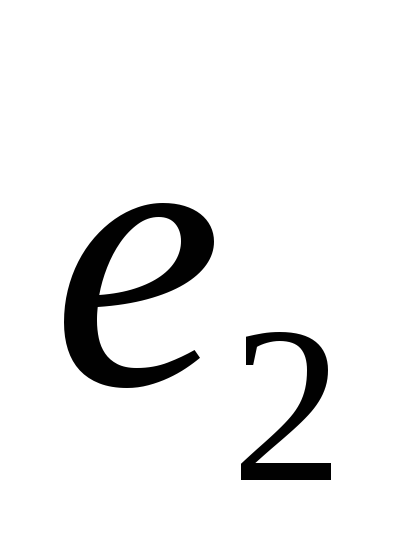если
известно,
что векторы
и
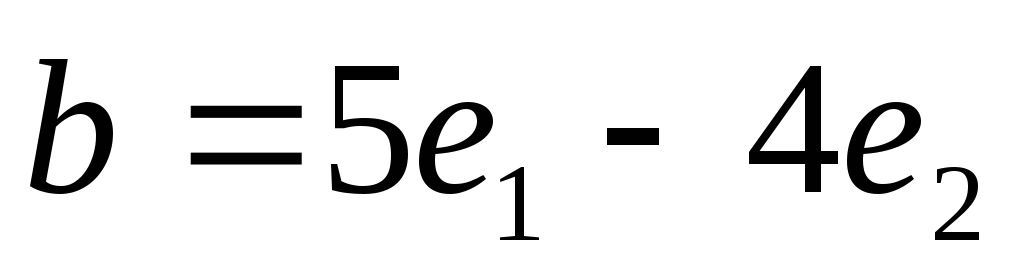взаимно
перпендикулярны. -
Доказать компланарность векторов
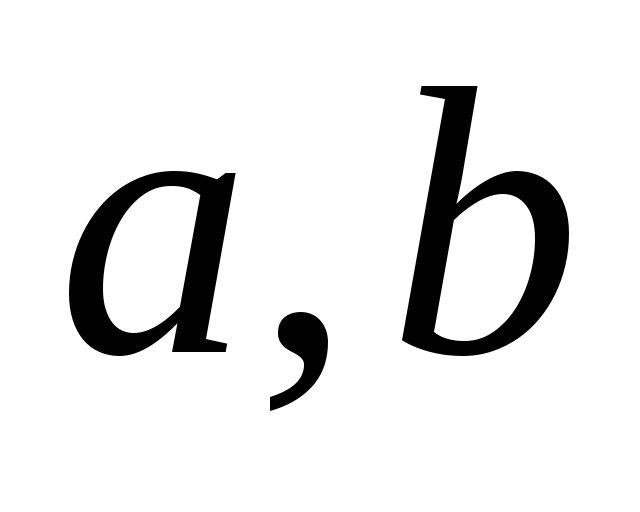и
,
зная, что
.
5) Доказать,
что уравнение плоскости, проходящей
через точки
и
перпендикулярно
плоскости
,
можно записать в виде
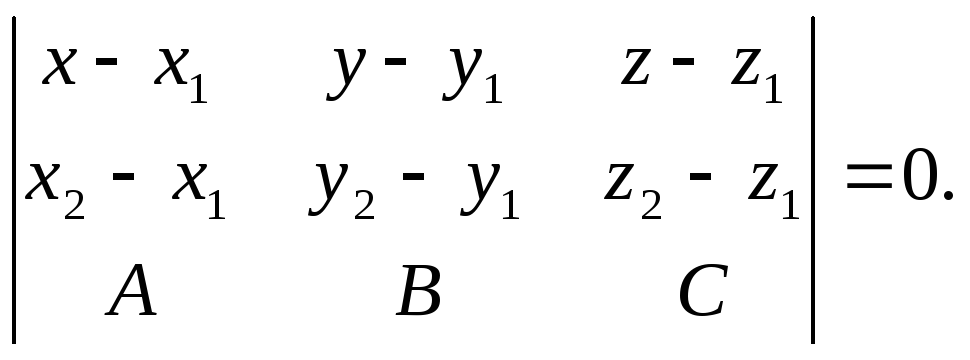
6)
Доказать, что уравнение плоскости,
проходящей через пересекающиеся
прямые
и
,
можно записать в виде
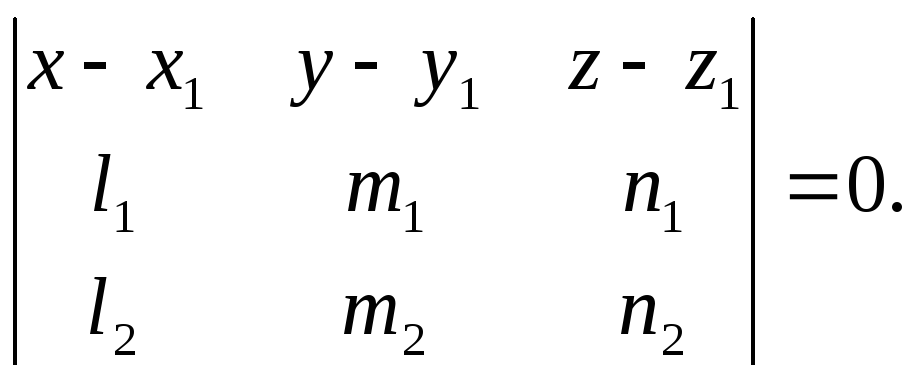
7)
Доказать, что уравнения прямой, проходящей
через точку
параллельно
плоскостям
и
,
можно записать в виде
-
Доказать, что необходимым и достаточным условием принадлежности двух прямых
и
,
одной плоскости является выполнение равенства
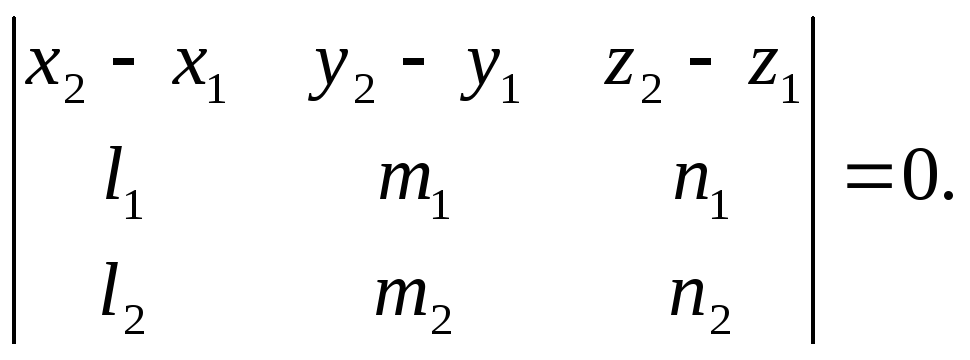
9)
Доказать, что расстояние от точки
до прямой, проходящей через точку
и имеющей направляющий вектор
,
определяется
формулой
10)
Даны две скрещивающиеся прямые,
проходящие соответственно через
точки
и
.
Их
направляющие векторы
и
известны. Доказать, что расстояние
между ними
определяется формулой
.
§ 9.3. РАСЧЕТНЫЕ ЗАДАНИЯ
Задача
1. Написать
разложение вектора
по
векторам
1.
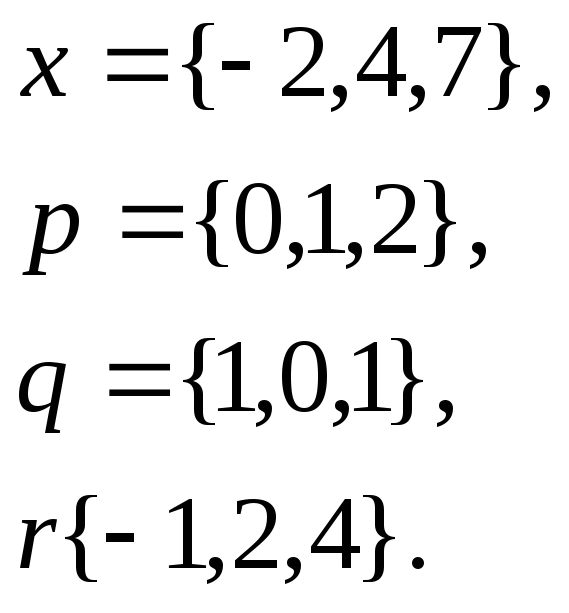
2.
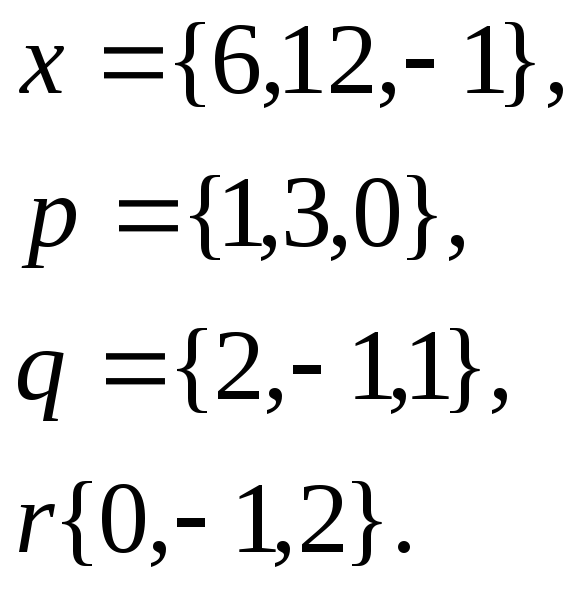
3.
4.
5.
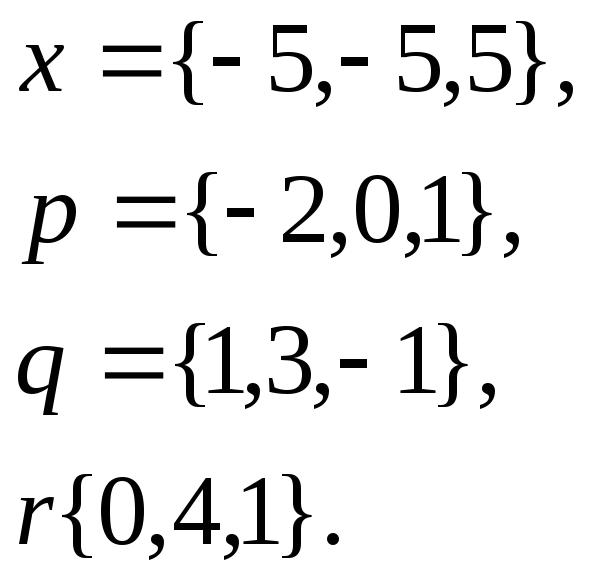
6.
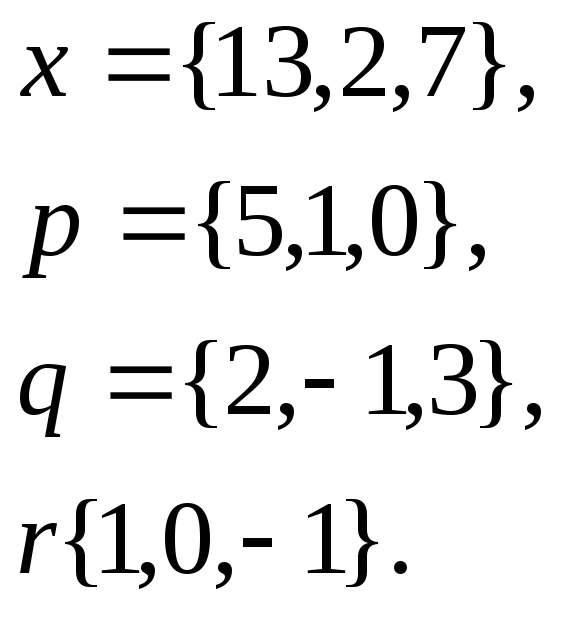
7.
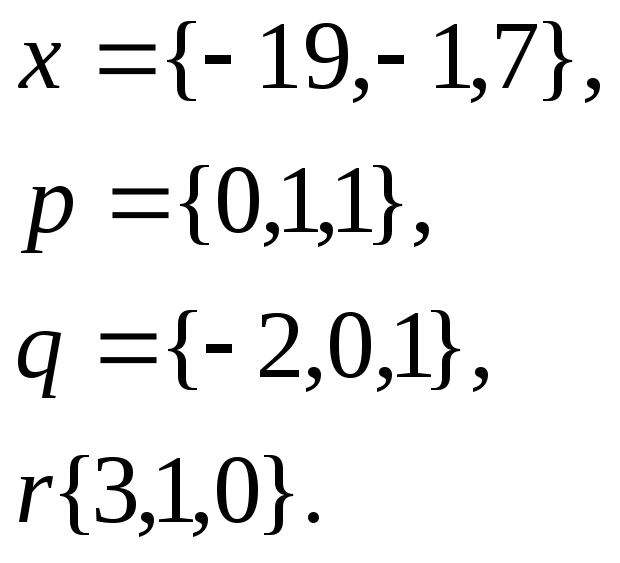
8.
9.
10.
11.
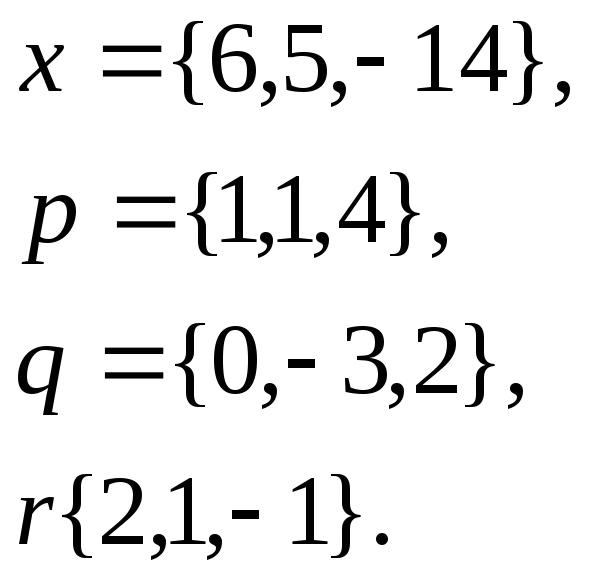
12.
13.
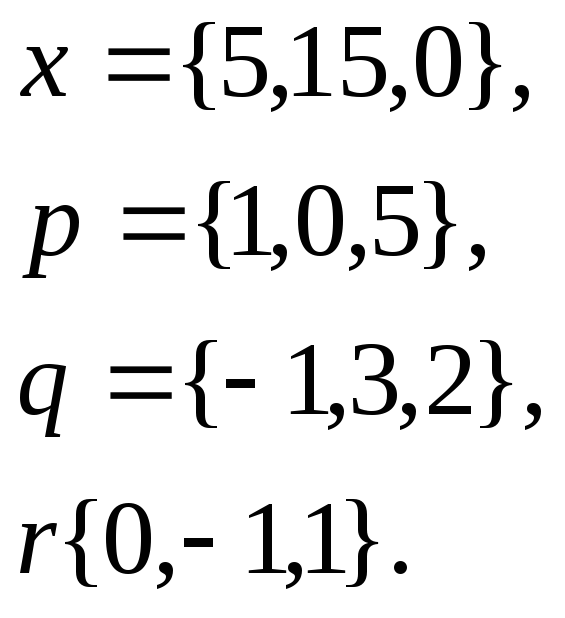
14.
15.
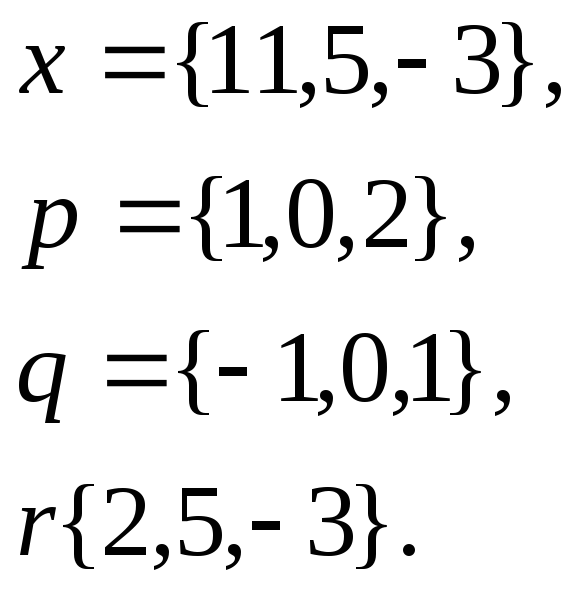
16.
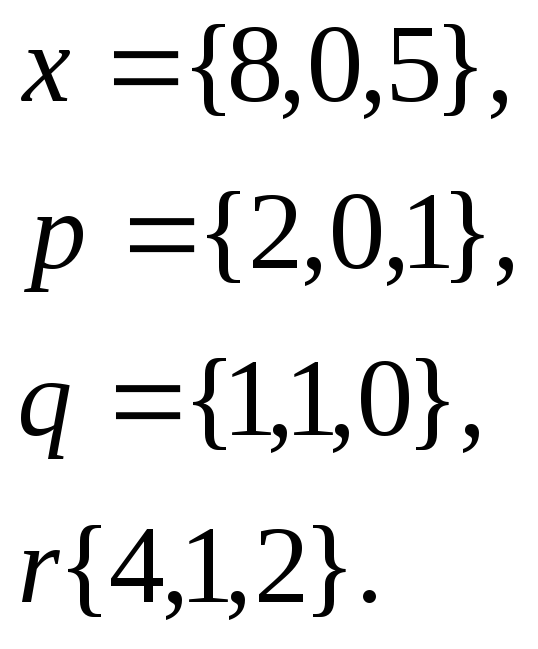
17.
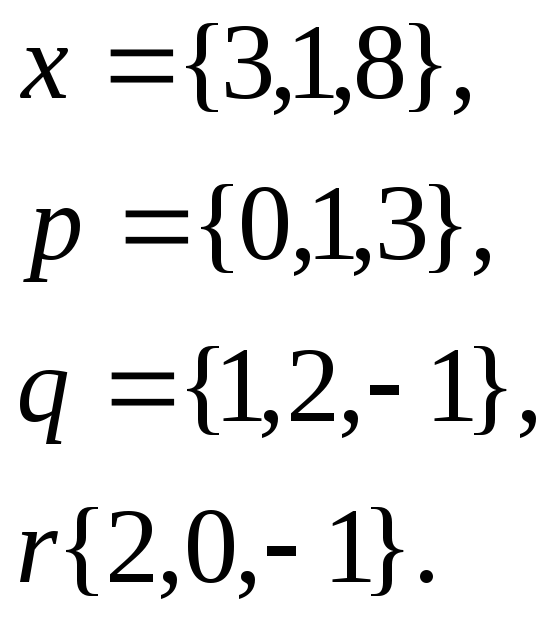
18.
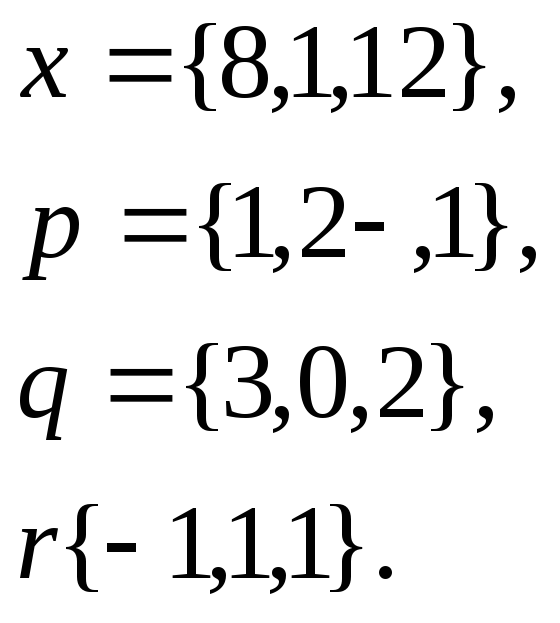
19.
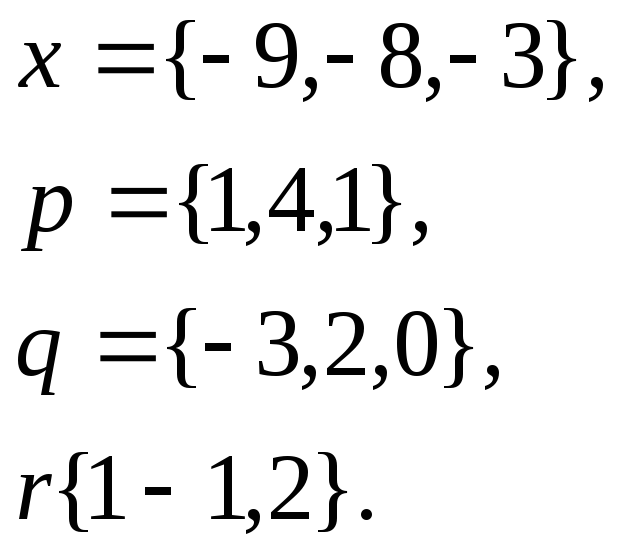
20.
21.
22.
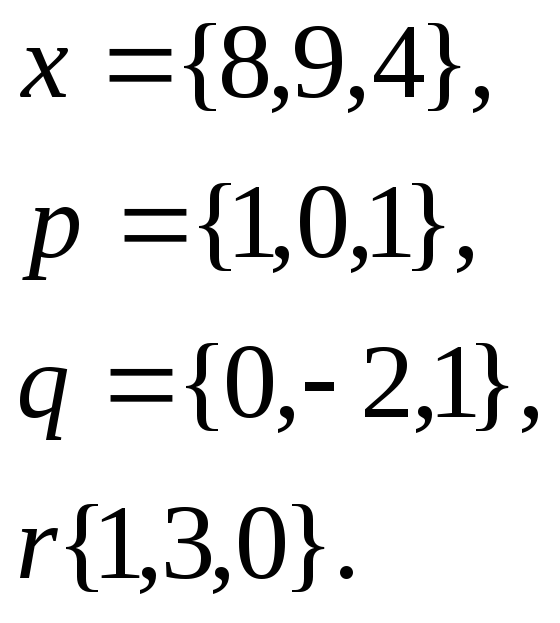
23.
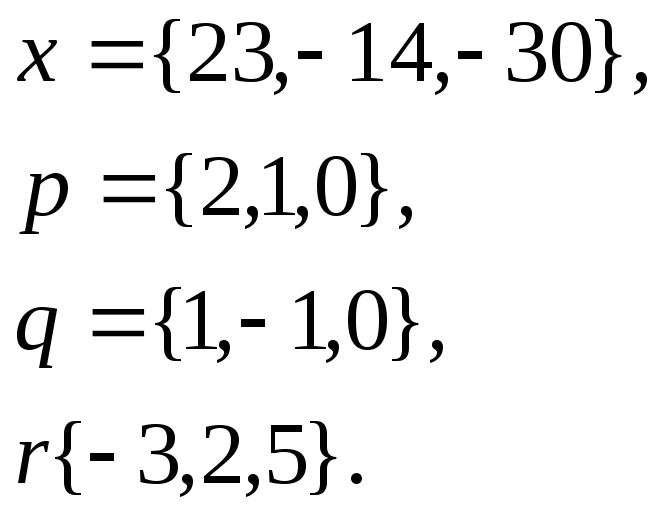
24.
25.
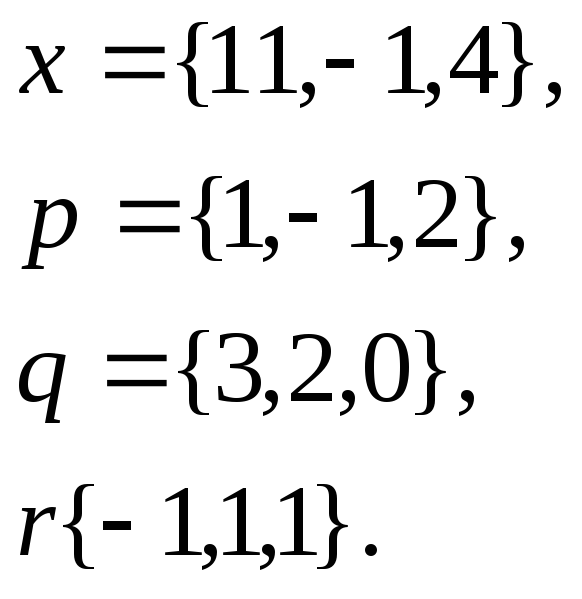
26.
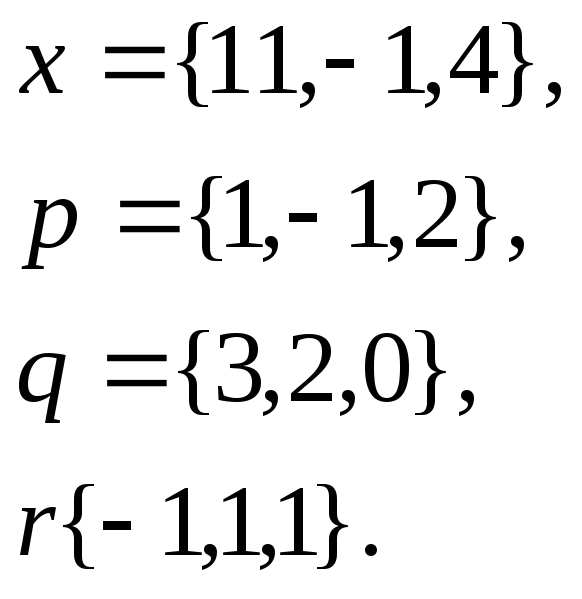
27.
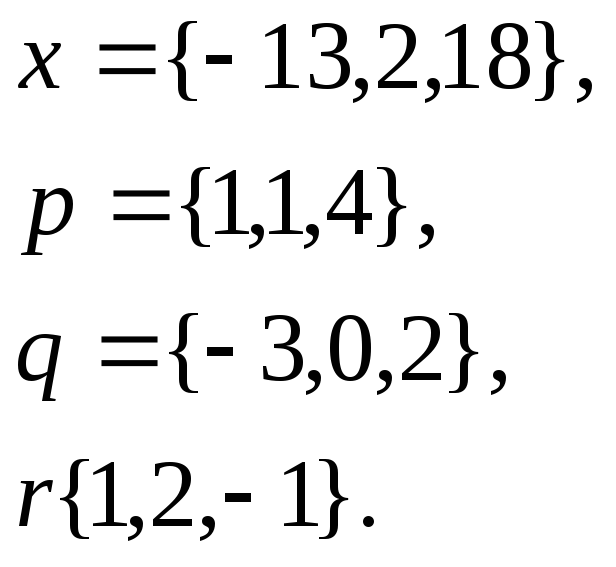
28.
29.
30.
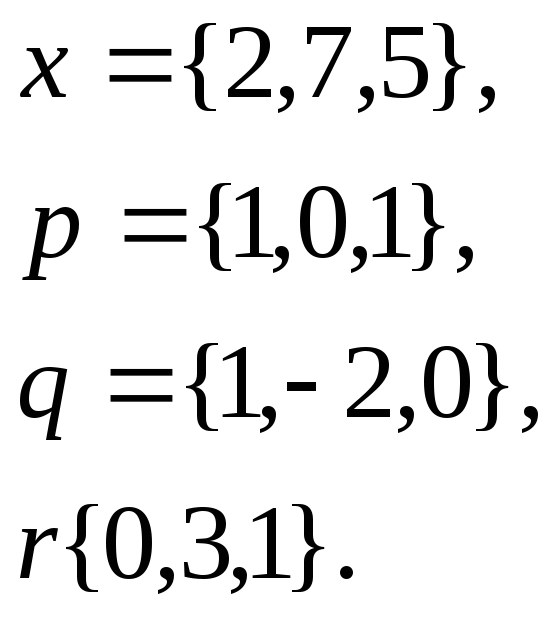
31.
Задача
2.
Коллинеарны ли векторы
и
,
построенные по векторам
и
?
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
Задача
3.
Найти косинус угла между векторами
и
.
1.
2.
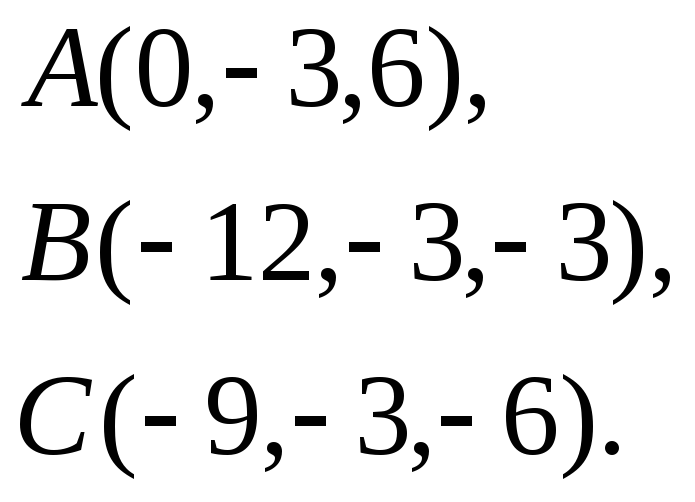
3.
4.
5.
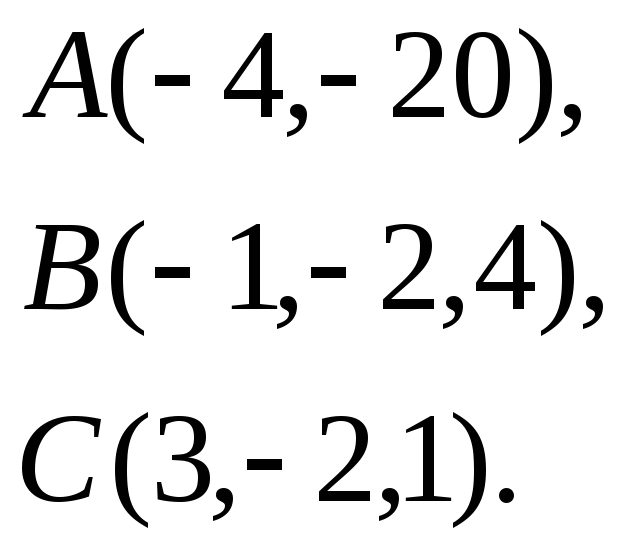
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
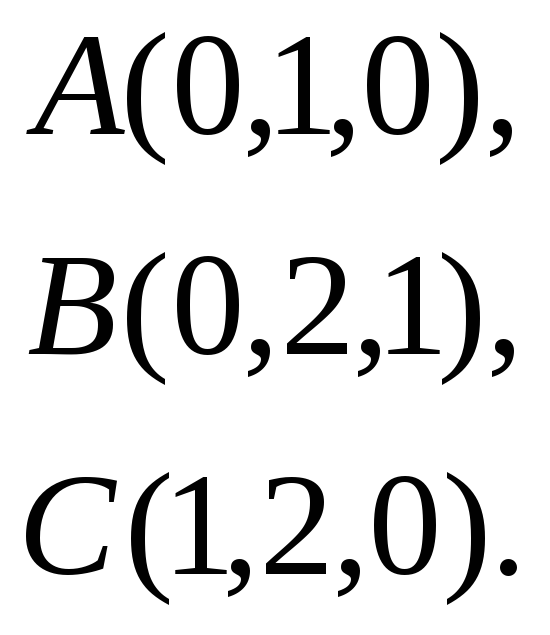
30.
31.
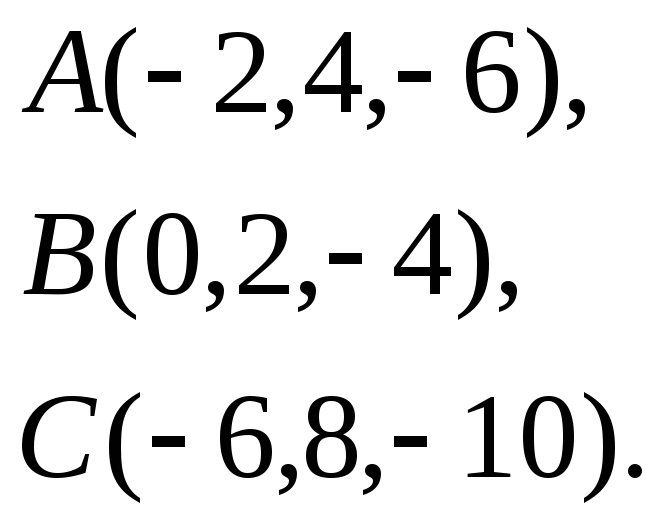
Задача
4. Вычислить
площадь параллелограмма, построенного
на векторах
и
.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
Задача
5. Компланарны
ли векторы
,
и
.
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
31.
Задача
6.
Вычислить объем тетраэдра с вершинами
в точках
и его высоту, опущенную из вершины
на грань
.
1.
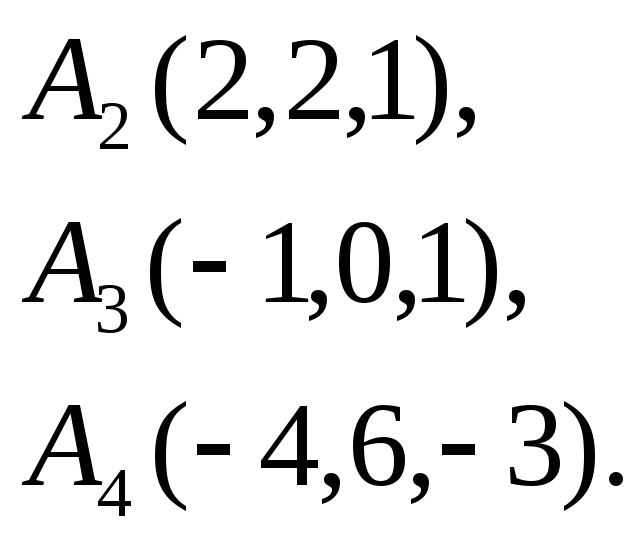
2.
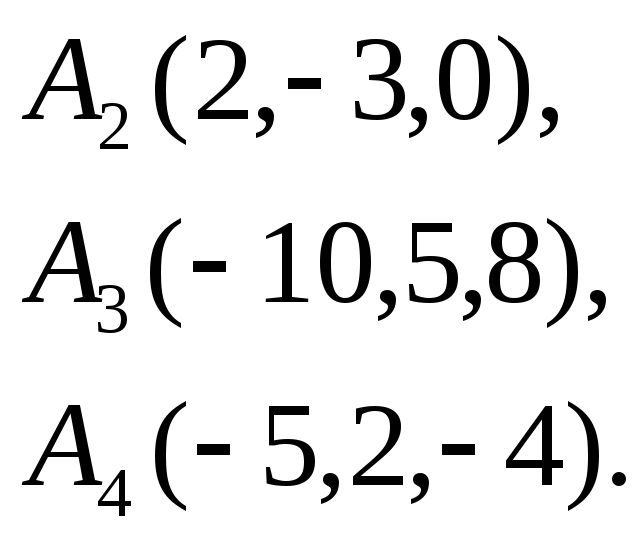
3.
4.
5.
6.
7.
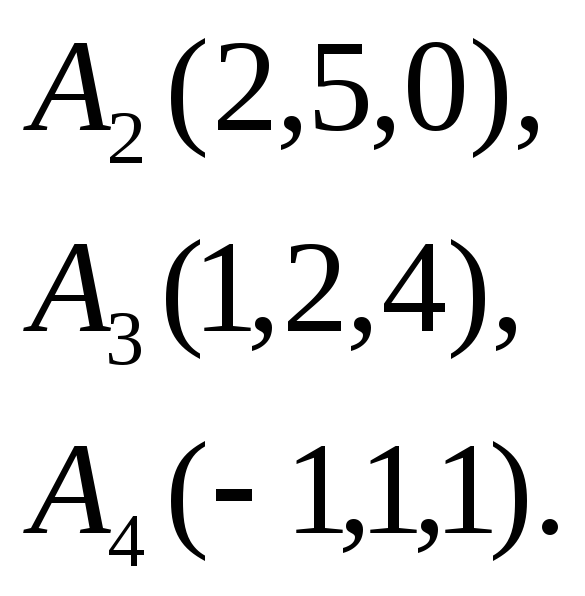
8.
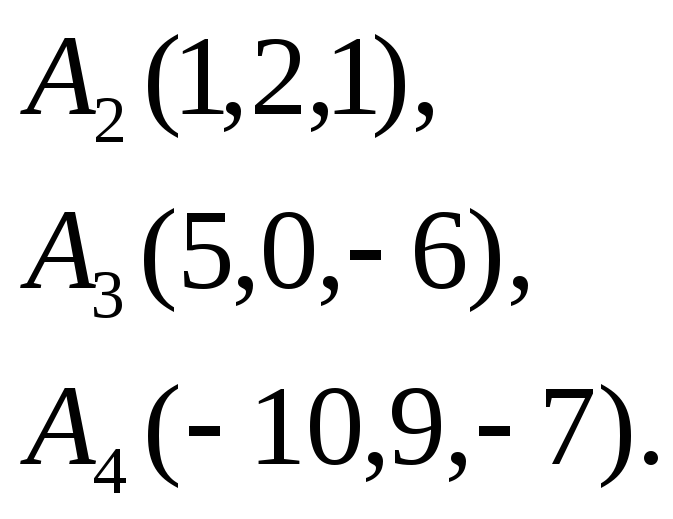
9.
10.
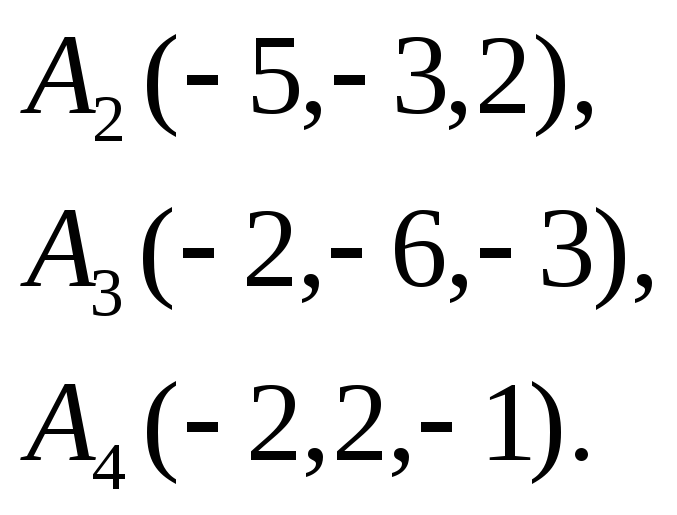
11.
12.
13.
14.
15.
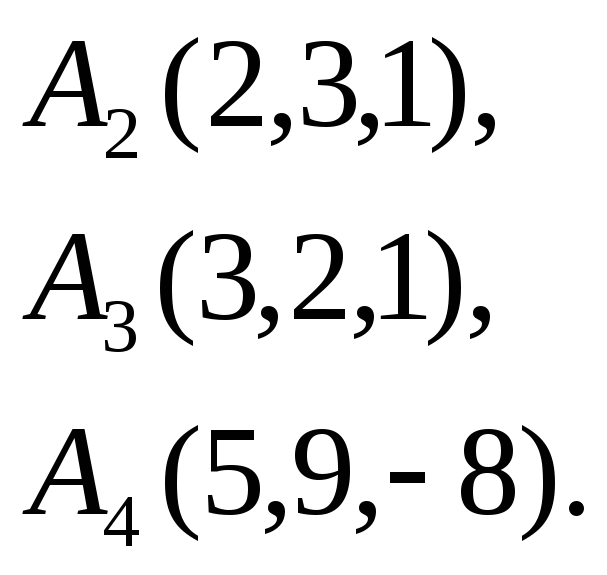
16.
17.
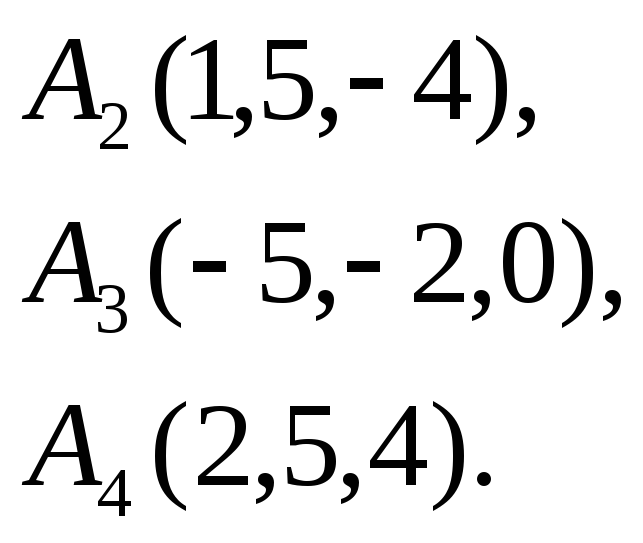
18.
19.
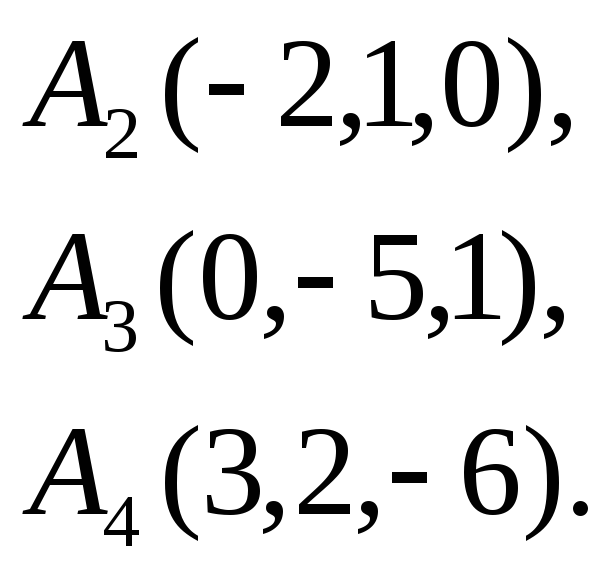
20.
21.
22.
23.
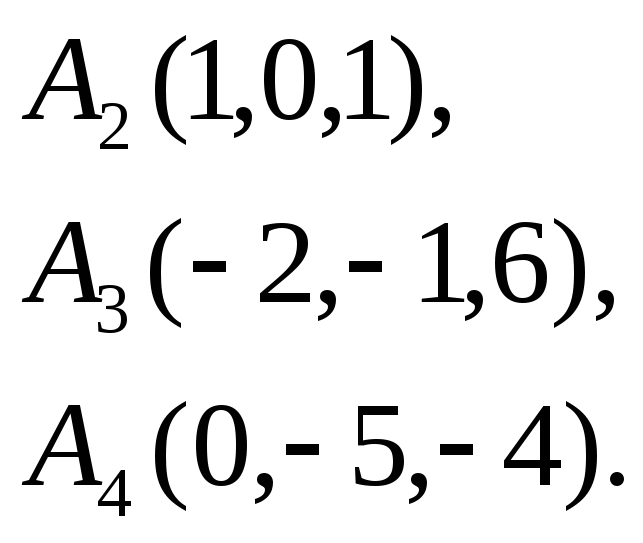
24.
25.
26.
27.
28.
29.
30.
31.
Задача
7. Найти
расстояние от точки
до
плоскости, проходящей через точки
.
1.
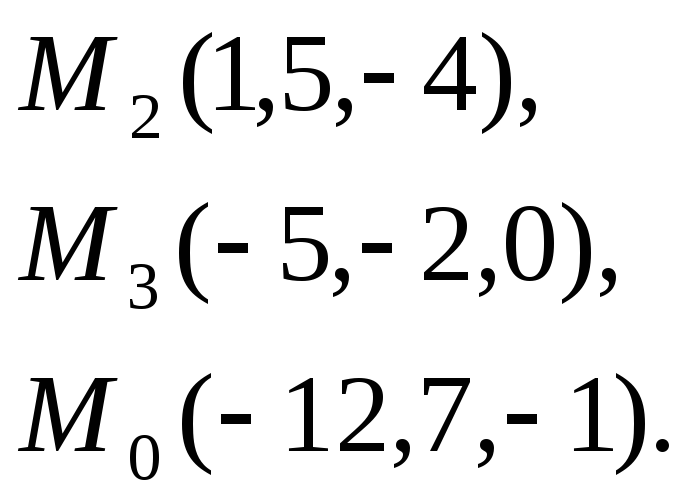
2.
3.
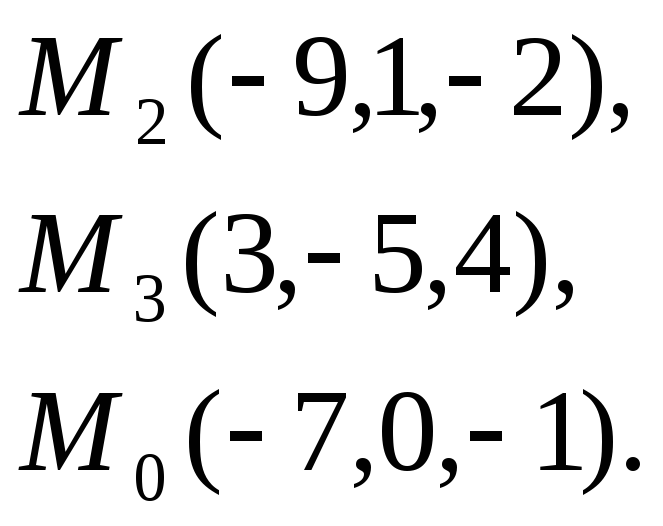
4.
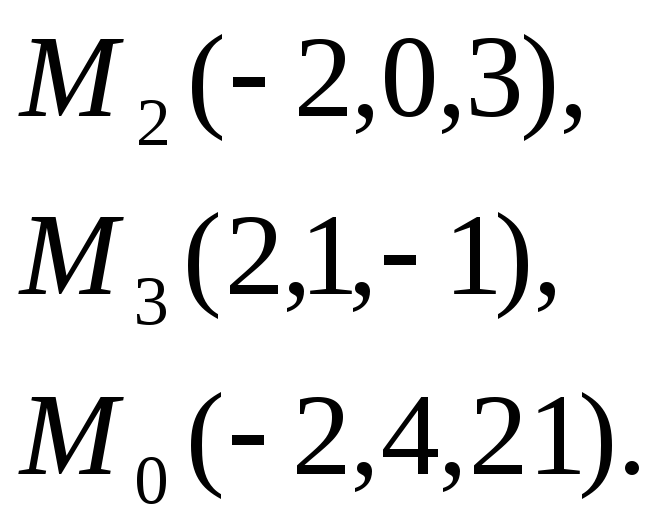
5.
6.
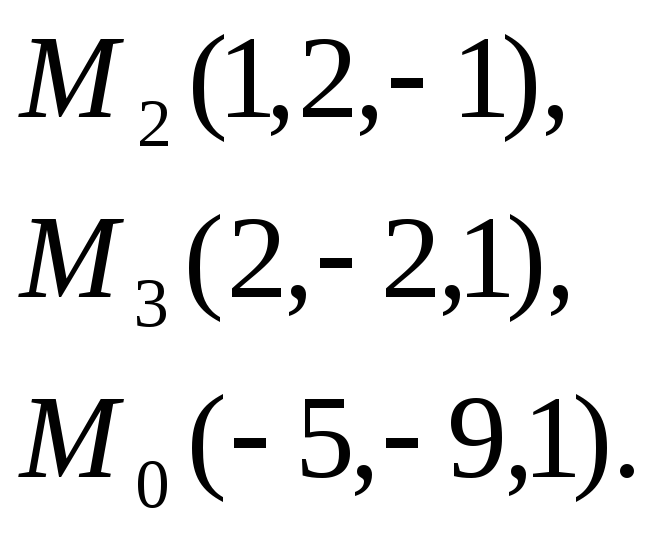
7.
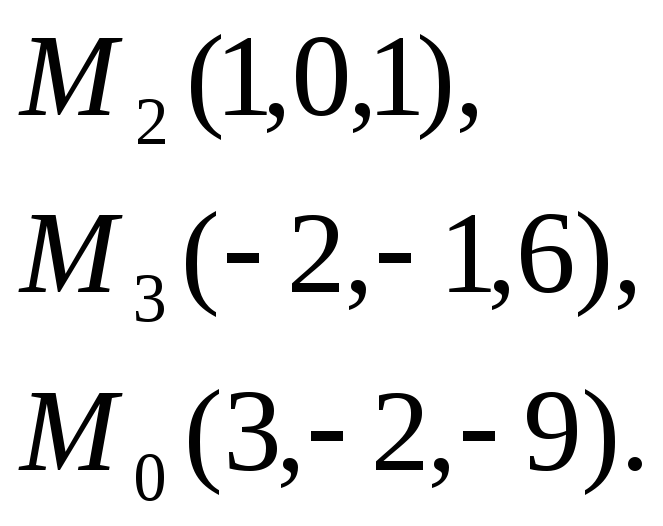
8.
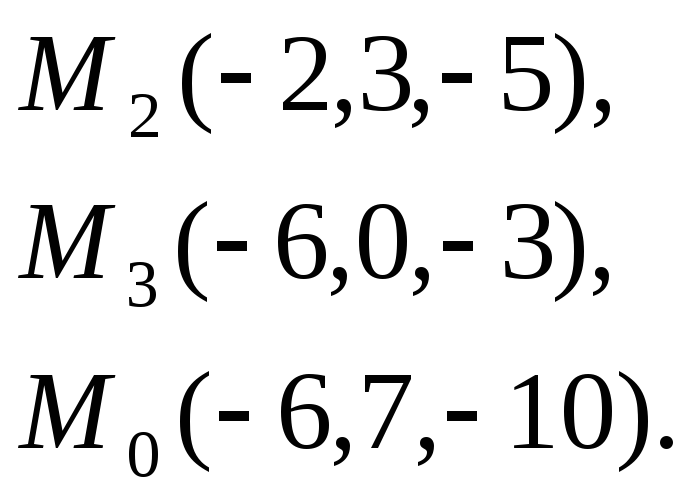
9.
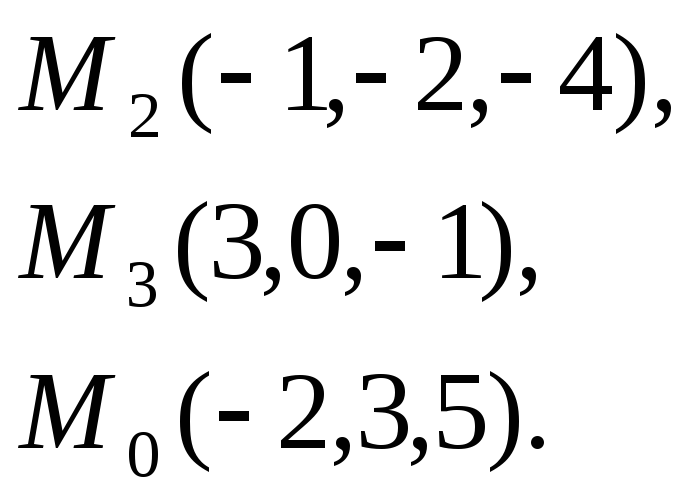
10.
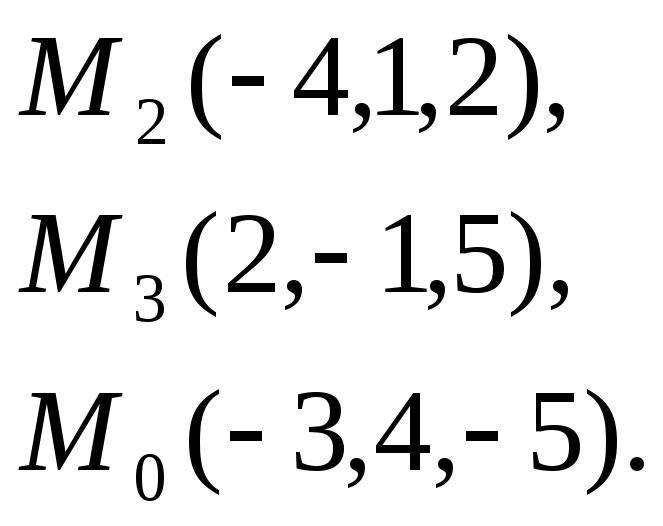
11.
12.
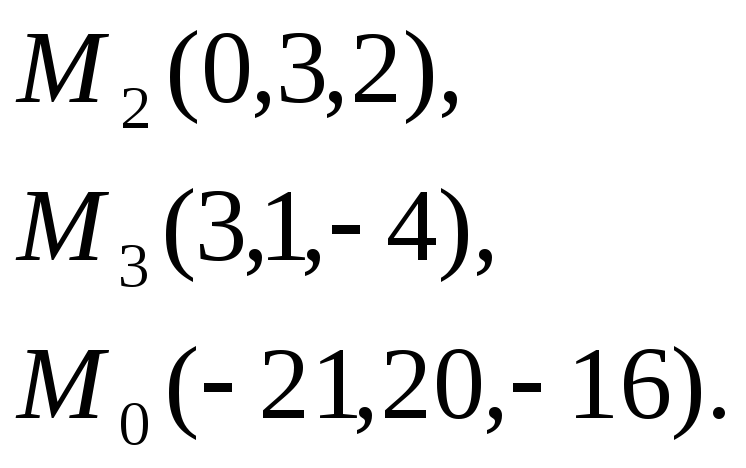
13.
14.
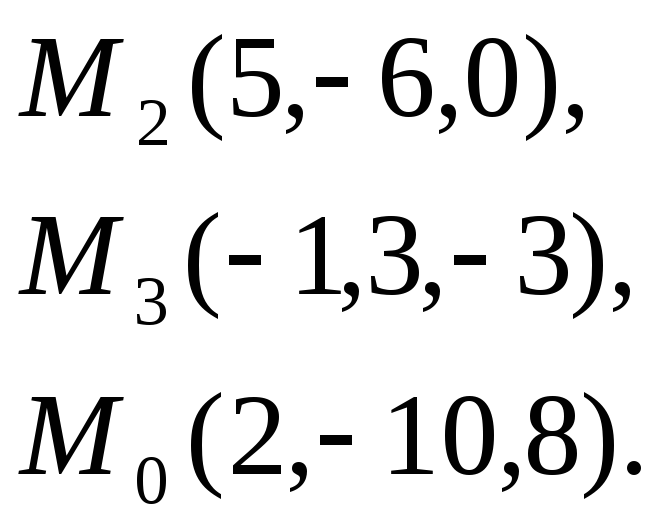
15.
