Определенный интеграл.Определение и свойства

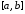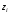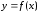Определение. Если существует конечный предел интегральной суммы (1) и он не зависит ни от способа разбиения отрезка на частичные отрезки, ни от выбора точек в них, то этот предел называется определенным интегралом от функции на отрезке 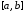и обозначается .

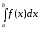Таким образом, .

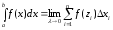Свойства

1. Значение определенного интеграла не зависит от обозначения переменной интегрирования: .

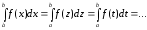2. Определенный интеграл с одинаковыми пределами интегрирования равен нулю:

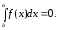
3. Если 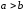, то, по определению, полагаем

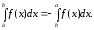
4. Постоянный множитель можно выносить за знак определенного интеграла:

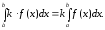
5. Определенный интеграл от алгебраической суммы двух функций равен алгебраической сумме определенных интегралов от этих функций:

.

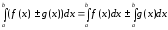3. Если функция 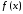интегрируема на 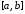и , то

.

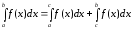3. (теорема о среднем). Если функция 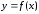непрерывна на отрезке 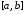, то на этом отрезке существует точка 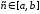, такая, что .

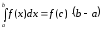Интеграл с переменным верхним пределом и его свойства.

Пусть на отрезке [ a, b ] задана непрерывная функция  f ( x ), тогда для любого x [ a, b ] существует функция:

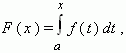
задаваемая  интегралом с переменным верхним пределом, стоящим в правой части равенства.

 

На интеграл с переменным верхним пределом распространяются все правила и свойства определённого интеграла. ( Лара свойства выше) :DD

Производная интеграла.Формула Ньютона-Лейбница.

Имеет место теорема: производная интеграла с переменным верхним пределом от непрерывной функции равна подынтегральной функции, в которой переменная интегрирования заменена верхним пределом:

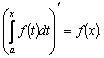
Формула Ньютона–Лейбница

Теорема. Если – какая–либо первообразная для непрерывной функции , то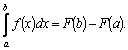

Замена переменной в определенном интеграле

При вычислении определенных интегралов с использованием формулы Ньютона-Лейбница предпочтительно жестко не разграничивать этапы решения задачи (нахождение первообразной подынтегральной функции, нахождение приращения первообразной). Такой подход, использующий, в частности, формулы замены переменной и интегрирования по частям для определенного интеграла, обычно позволяет упростить запись решения.

ТЕОРЕМА. Пусть функция φ(t) имеет непрерывную производную на отрезке [α,β], а=φ(α), в=φ(β) и функция f(х) непрерывна в каждой точке х вида х=φ(t), где t[α,β].

Тогда справедливо следующее равенство:

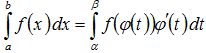
Эта формула носит название формулы замены переменной в определенном интеграле.

Интегрирование по частям

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

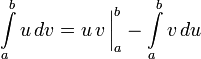
Определение и вычисление длины кривой

определение

Длина кривой (или, что то же, длина дуги кривой) в метрическом пространстве — числовая характеристика протяжённости этой кривой^]. Исторически вычисление длины кривой называлось спрямлением кривой (от лат. rectificatio, спрямление). Если длина кривой существует и конечна, то говорят, что кривая спрямляемая, в противном случае — неспрямляемая.

Вычисление

В математическом анализе выводится формула для вычисления длины s отрезка кривой, заданной уравнениями (1), при условии, что все три функции непрерывно дифференцируемы:

(2)

Дифференциал длины дуги

Дифференциал длины дуги

     В декартовых координатах:

     В полярных координатах:

Несобственные интегралы с бесконечными пределами и от неограниченных функций.

Пусть функция f(x) непрерывна при a ≤ x < +∞. Тогда по определению полагают

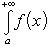
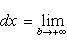
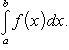     (2)

Если предел (2) существует, то несобственный интеграл с бесконечным пределом интегрирования, стоящий в левой части равенства (2), назвается сходящимся и его значение определяется формулой (2); в противном случае равенство (2) теряет смысл, несобственный интеграл, стоящий слева, называется расходящимся и ему не приписывается никакого числового значения.

     Интеграл определяется аналогично:

     (3)

а интеграл

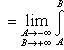
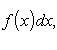     (4)

при этом

     (5)

где a - любое число.

Абсолютная и условная сходимость несобственных интегралов.

Сходящийся ряд называется сходящимся абсолютно, если сходится ряд из модулей , иначе — сходящимся условно.

Аналогично, если несобственный интеграл от функции сходится, то он называется сходящимся абсолютно или условно в зависимости от того, сходится или нет интеграл от ее модуля .

Условная сходимость

Интеграл 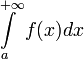называется условно сходящимся, если 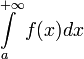сходится, а 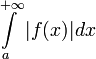расходится.

Определение ф н.порядка.Область определения.

ОПРЕДЕЛЕНИЕ. Пусть 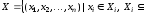ℝ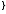. Функция, заданная на множестве 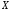и имеющая областью значений множество 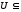ℝ, называется функцией переменных.

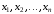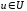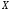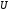При этом называются независимыми переменными (аргументами), переменная называется зависимой переменной или функцией, множество – областью определения функции, множество – областью значений функции.

Предел,непрерывность,частные производные.

предел.

Пусть функция такова, что её область определения содержит целиком некоторое окончание базы . Число называется пределом функции по базе , если для любого, сколь угодно малого, числа найдётся такое окончание базы , что при всех выполняется неравенство . Число обозначается тогда

 Непрерывность.   

Функция u = f(x) называется непрерывной в точке a, если

lim x → a f(x) = f(a).

Частные производные

Определение Если существует , то он называется частной производной функции u=f(x₁, ..., x_m) в т. М(x₁, ..., x_m) по аргументу x_k и обозначается одним из символов: . Таким образом, .

Полный дифференциал,его связь с частными производными.

Полный дифференциал, функции f (x, у, z,...) нескольких независимых переменных — выражение , в случае, когда оно отличается от полного приращения Df = f (x + Dx, y + Dy, z + Dz,…) - f (x, y, z, …) на величину, бесконечно малую по сравнению с

В выражении дифференциала d z = A·Δ x + B·Δ y величины А и В равны частным производным функции по соответствующим переменным:

  и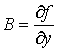  

Достаточное условие дифференцируемости

Если функция u = f(x1, x2,  … , xn) дифференцируема в точке a , то в этой точке существуют частные производные по каждому аргументу x1,  … , xn , причем

∂u ∂xk  (a) = Ak,

где Ak — числа в определении (1).

Достаточное условие дифференцируемости:

Теорема . Если функция u = f(x) имеет в окрестности точки a частные производные, непрерывные в этой точке, то f(x) дифференцируема в точке a .

Сложные функции и их производные????????

Инвариативность формы первого дифференциала.

Рассмотрим сложную функцию y=f(u(x)). Пусть функции y=f(u), u=u(x) дифференцируемы, тогда Таким образом, если аргументом функции является функция другого аргумента, то форма дифференциала совпадает с формой дифференциала , когда аргументом функции является независимая переменная. Это свойство называется инвариантностью формы дифференциала

Неявная функция.Теорема существования

Неявные функции-это функции, заданные соотношениями между независимыми переменными, не разрешенными относительно последних; эти соотношения являются одним из способов задания функции.

Теорема существования

Неявные функции в её простейшей формулировке утверждает, что если функция F (x, y) обращается в нуль при паре значений х = x₀, у = y₀ [F (x₀, y₀) ¹ 0] и дифференцируема в окрестности точки (x₀, y₀), причём F’_x (х, у) и F’_y (х, у) непрерывны в этой окрестности и F’_y (x₀, y₀) ¹ 0, то в достаточно малой окрестности точки x₀ существует одна и только одна однозначная непрерывная функция у = у (х), удовлетворяющая соотношению F (x, y) = 0 и обращающаяся в y₀ при x = x₀; при этом y"(x) = —F’_x (x, y)/F’_y (x, у).   Для приближённого вычисления значений Неявные функции вблизи точки x₀, где её значение y₀ уже известно, широко применяются степенные ряды. Так, если F (x, у) — аналитическая функция [т. е. может быть разложена в окрестности точки (x₀, y₀) в сходящийся двойной степенной ряд] и F’_y (x₀, y₀) ¹ 0, то Неявные функции, заданная соотношением F (x, y) = 0, может быть получена в виде степенного ряда