Экстремум функции.Необходимые и достаточные условия существования экстремума

Точка x_о называется точкой локального максимума (минимума) функции f(x), если существует окрестность точки x_о, для всех точек которой верно неравенство f(x)  f(x_о) (f(x) ³ f(x_о)). Точки максимума и минимума называются точками экстремума, а значения функции в этих точках - ее экстремумами. Необходимые условия экстремума.

Первое достаточное условие. Пусть x_о - критическая точка. Если f  (x) при переходе через точку x_о меняет знак плюс на минус, то в точке x_о функция имеет максимум, в противном случае - минимум. Если при переходе через критическую точку производная не меняет знак, то в точке x_о экстремума нет. Второе достаточное условие. Пусть функция f(x) имеет производную f ¢ (x) в окрестности точки x_о и вторую производную  в самой точке x_о. Если f (x_о) = 0, >0 (<0), то точка x_о является точкой локального минимума (максимума) функции f(x). Если же =0, то нужно либо пользоваться первым достаточным условием, либо привлекать высшие производные. На отрезке [a,b] функция y = f(x) может достигать наименьшего или наибольшего значения либо в критических точках, либо на концах отрезка [a,b].

Выпуклая функция

В математике функция называется выпуклой (или выпуклой вниз) на некотором интервале (в общем случае на выпуклом подмножестве некоторого векторного пространства), если для любых двух точек x, y из этого интервала и для любого числа t, принадлежащего отрезку [0,1], выполняется неравенство

Если это неравенство является строгим для всех t из интервала (0,1), функция называется строго выпуклой; если выполняется обратное неравенство, функция называется вогнутой, или выпуклой вверх

Достаточное условие выпуклости

Точки перегиба.Необходимое и достаточное условие точки перегиба

Точка, в которой функция определена и в которой функция меняет направление выпуклости, называется точкой перегиба.    

Необходимое условие

Теорема. Пусть функция y = f (x) дважды непрерывно дифференцируема на интервале (a, b). Для того, чтобы точка М(x₀, f(x₀)) была точкой перегиба графика функции y = f (x) необходимо, чтобы f " (x₀) = 0.    Достаточное условие

Теорема. Пусть функция y = f (x) имеет вторую производную f "(x) в некоторой достаточно малой окрестности точки x₀ интервала (a, b), за исключением, быть может самой точки х₀, а график функции имеет касательную в точке С = (х₀, f (x₀)). Если при переходе через точку х₀ вторая производная f "(x) меняет знак, то точка С является точкой перегиба графика функции y = f (x).    

Асимптоты графика функции

  Вертикальной асимптотой графика функции называется вертикальная прямая , если или при каком-либо из условий: , , .

Первообразная

Первообра́зной или примити́вной функцией (иногда называют также антипроизводной) данной функции f называют такую F, производная которой (на всей области определения) равна f, то есть F ′ = f. Вычисление первообразной заключается в нахождении неопределённого интеграла, а сам процесс называется интегрированием.

Так, например, функция является первообразной . Так как производная константы равна нулю, будет иметь бесконечное количество первообразных;

Неопределенный интеграл и его свойства

Множество первообразных функции f(x) называется неопределённым интегралом от этой функции и обозначается символом .

Свойства неопределённого интеграла,:

1. .

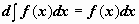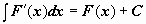2. (или ).

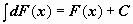Таблица основных интегралов

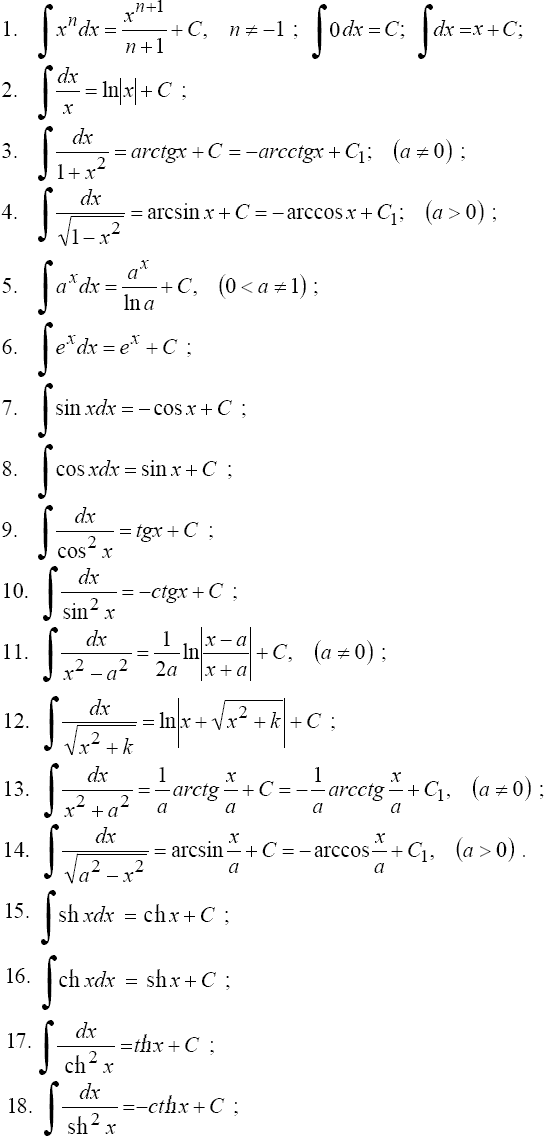
Простейшие приемы интегрирования:непосредственное интегрирование,замена переменной(подведение под знак дифференциала и подстановка),интегрирование по частям.

Непосредственное интегрирование

Метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам, называется непосредственным интегрированием.

замена переменной(подведение под знак дифференциала и подстановка)

Метод интегрирования подстановкой заключается во введении новой переменной интегрирования (то есть подстановки). При этом заданный интеграл приводится к новому интегралу, который является табличным или к нему сводящимся. Общих методов подбора подстановок не существует. Умение правильно определить подстановку приобретается практикой.

интегрирование по частям

Интегри́рование по частя́м — один из способов нахождения интеграла. Суть метода в следующем: если подынтегральная функция может быть представлена в виде произведения двух непрерывных и гладких функций (каждая из которых может быть как элементарной функцией, так и композицией), то справедливы следующие формулы

для неопределённого интеграла:

для определённого:

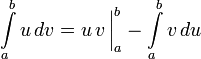
Разложение рациональной функции на простейшие дроби

Пусть знаменатель правильной рациональной дроби может быть представлен в виде (множителей вида может быть несколько), где — заданные числа

трехчленне имеет действительных корней.

Тогдапредставляется в виде суммы простейших дробей

1—3 типов:

где— неизвестные коэффициенты, которые находятся путем приведения суммы справа к общему знаменателю и последующего приравнивания полученного числителя к

Интегрирование рациональной функции

Для интегрирования рациональной функции , где P(x) и Q(x) - полиномы, используется следующая последовательность шагов:

1. Если дробь неправильная (т.е. степень P(x) больше степени Q(x)), преобразовать ее в правильную, выделив целое выражение;

2. Разложить знаменатель Q(x) на произведение одночленов и/или несократимых квадратичных выражений;

3. Разложить рациональную дробь на простейшие дроби, используя метод неопределенных коэффициентов;

4. Вычислить интегралы от простейших дробей.

Интегрирование тригонометрических и иррациональных функций

Интегрирование ирррациональных функций

Для интегрирования иррациональной функции, содержащей используется подстановка . Чтобы проинтегрировать иррациональную функцию, содержащую несколько рациональных степеней x, применяется подстановка в форме , где n полагается равным наименьшему общему кратному знаменателей всех дробных степеней, входящих в данную функцию..

Интегрирование тригонометрических функций

Интегралы вида  вычисляются с помощью замены  . Интегралы вида  вычисляются с помощью замены  . Интегралы вида  , если , то есть четная рациональная функция своих аргументов вычисляются с помощью замены    .

Интегралы вида  вычисляются с помощью формул понижения степени  .
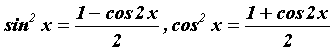