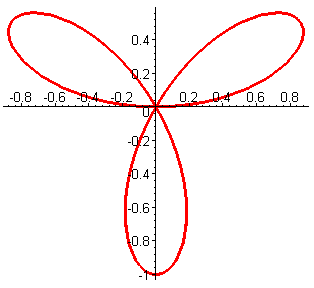11.5. Полярные координаты.

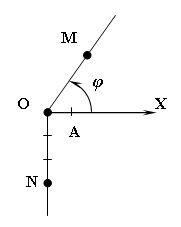
Возьмём на плоскости (рис. 11.8) произвольную точку О (полюс) и проведём луч ОХ (полярная ось). Примем какой-либо отрезок ОА за единицу длины и радиан за единицу измерения углов. Тогда положение любой точки М на плоскости можно задать двумя числами: положительным числом , выражающим длину отрезка ОМ (полярный радиус) и числом , выражающим величину угла ХОМ (полярный угол). Числа иназываютсяполярными координатами точки М.

На рис. 11.8 полярные координаты определяют точкуN, полярные координаты – ту же точкуN. Полярные координаты ,(также,и т.д.) определяют точкуA. Каждой паре значений отвечает только одна точкаM, но одной и той же точке M отвечает бесчисленное множество значений полярного угла, отличающихся друг от друга на число, кратное . Если же точкаM совпадает с полюсом, то значение полярного угла остаётся произвольным.

Рис. 11.8.

Условно выделяется главное значение полярного угла . Точкесоответствует главное значение полярного угла. При введении главных значений каждой точке (кроме полюса) отвечает одна пара полярных координат. Для полюса,остаётся произвольным.

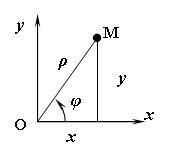
Связь между полярными и прямоугольными координатами определяется следующими формулами (рис. 11.9): , . (11.1) И обратно: , ,. (11.2)
	Рис. 11.9.

 Пример 11.5. 1) Дана точка . Найдём её полярные координаты:

, ,.

Таким образом, угол и в полярной системе координат точка.

2) Представим уравнение окружности , заданное в прямоугольной системехОy, в полярной системе координат. Используя формулы (11.1), получаем или.

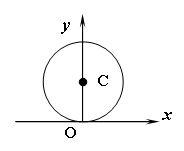
3) Определим, какую линию представляет уравнение .

Переходя к прямоугольным координатам по формулам (11.2), находим , то есть или. Получили уравнение окружности радиуса а, проходящей через полюс О и касающейся полярной оси ОХ (рис. 11.10). 
	Рис. 11.10.

 Пример 11.6. Рассмотрим несколько кривых, которые описываются функциями, заданными в полярной системе координат.

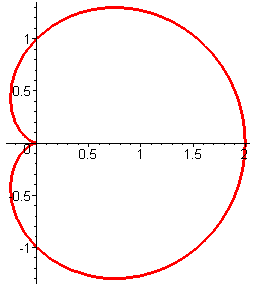
Трёхлепестковая роза описывается уравнением .	Кардиоида описывается уравнением .
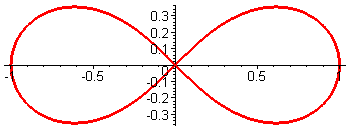
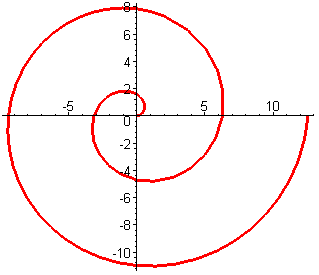
Лемниската Бернулли: .	Спираль Архимеда. Её уравнение: .



53