11.4. Классификация функций.

Определение 11.10. Функция называется явной, если она задана формулой, в которой правая часть не содержит зависимой переменной. Например .

Функция у аргумента х называется неявной, если она задана уравнением , неразрешённым относительно зависимой переменной. Например, функция у, заданная уравнением.

Определение 11.11. Пусть есть функция от независимой переменной х, определённой на промежутке Х с областью значенийY. Поставим в соответствие каждому единственное значение, при котором. Тогда полученная функция, определённая на промежуткеY с областью значений Х, называется обратной функцией. Так как традиционно независимую переменную обозначают через х, а функцию через у, то функция, обратная к функции , примет вид. Обратную функциюобозначают также в виде.

Для любой строго монотонной функции существует обратная функция. Графики взаимно обратных функций симметричны относительно биссектрисы первого и третьего координатных углов.

Определение 11.12. Пусть функция есть функция от переменнойu, определённой на множестве U с областью значений Y, а переменная u в свою очередь является функцией от переменной х, определённой на множестве Х с областью значенийU. Тогда заданная на множестве Х функция называетсясложной функцией (или композицией функций).

Из основных функций новые функции могут быть получены при помощи алгебраических действий и операций образования сложной функции.

Определение 11.13. Функции, построенные из основных функций с помощью конечного числа алгебраических действий и конечного числа операций образования сложной функции, называются элементарными функциями.

Например, функция является элементарной, так как здесь число операций алгебраических действий и образования сложной функции конечно.

Примерами неэлементарных функций являются функции ,, функция Дирихле.

Определение 11.14. Функция называется алгебраической, если над аргументом проводится конечное число алгебраических действий. К числу алгебраических функций относятся целая рациональная функция (многочлен) ;дробно-рациональная функция – отношение двух многочленов; иррациональная функция – в составе операций над аргументом имеется извлечение корня.

Всякая неалгебраическая функция называется трансцендентной. К числу трансцендентных относятся функции: показательная, логарифмическая, тригонометрические, обратные тригонометрические, функция Дирихле и т.п.

Определение 11.15. Если на некотором множестве заданы две функциии, то множество всех точек на плоскости хОy с координатами , где , называется кривой, заданной параметрически. Кривая, заданная параметрически, является графиком функции, заданной параметрически.

 Пример 11.4. 1) Рассмотрим астроиду. Данная кривая является графиком функции 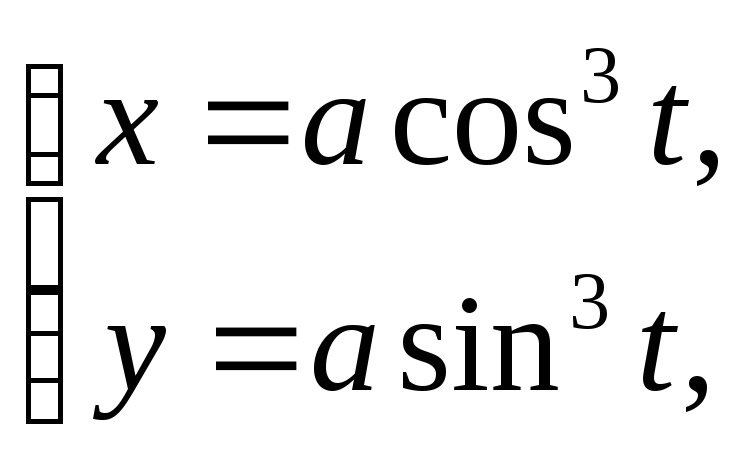заданной параметрически (рис. 11.6).

Рис. 11.6.

2) Рассмотрим циклоиду, она является графиком параметрически заданной функции 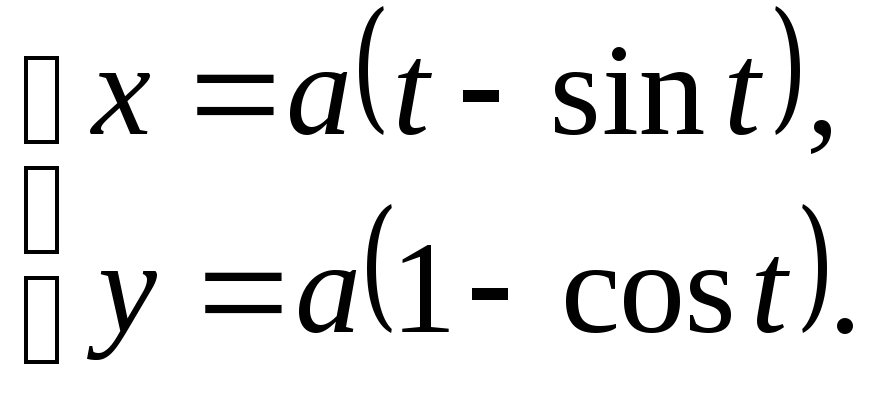Эта функция описывает траекторию точки на окружности, катящейся без скольжения по прямой линии (рис. 11.7).

Рис. 11.7.

