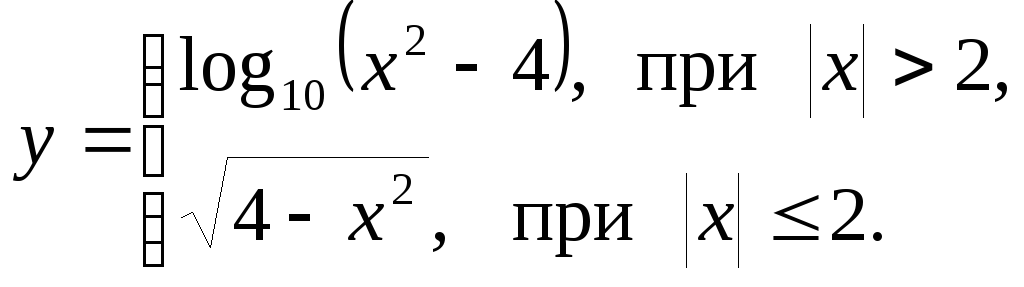Лекция 11. Функция одной переменной.

11.1. Понятие функции (отображения).

Определение 11.1. Пусть дано множество и. Если указан некоторый способf каждому элементу поставить в соответствие элемент, тогда соответствие(или) называетсяфункцией с областью определения X и областью значений Y.

x – независимая переменная, аргумент;

y – зависимая переменная, значение функции.

☼ Замечание 11.1. Определение 11.1 не требует, чтобы каждый был значением при некотороми чтобы разнымx соответствовали разные y. В этом случае имеем взаимно однозначное соответствие, функция однозначна. ☼

Определение 11.2. Если область значений Y функции есть числовая осьR (расширенная числовая ось ), тоназываютчисловой функцией или функцией вещественного переменного. Если Y есть векторное пространство , то функцияназываетсявекторной функцией. Если X есть множество натуральных чисел N, то функция , обозначаемаяилиf_n, называется последовательностью точек множества Y.

☼ Замечание 11.2. Последовательность точек множества не сводится к понятию подмножества: в последовательности точки могут повторяться, а в подмножестве нет.

Так, например, если ,с – подмножество, состоящее из одного элемента, а последовательность имеет бесконечно много элементов. ☼

Определение 11.3. Прямым произведением множеств X и Y назовём множество всех пар, где первый элемент взят изX, второй - из Y.

.

Подмножество при фиксированномy₀ называется слоем в , отвечающим элементу y₀. .

–множество всех отображений :.

Определение 11.4. Графиком функции с областью определенияX и областью значений Y назовем подмножество прямого произведения , состоящее из тех пар, для которых, то есть.

При иимеем обычное определение графика вещественной функции числового аргумента.

11.2. Способы задания функций.

Существует несколько способов задания функции: аналитический, графический, табличный, словесный.

Аналитический способ описывает функцию формулой. Например:

а) ,
б) ,
в) ,
г)

Не следует смешивать функцию с её аналитическим выражением. В данном примере одна функция имеет два аналитических выражения: приипри. На рис. 11.1 изображён график этой функции.

Рис. 11.1.

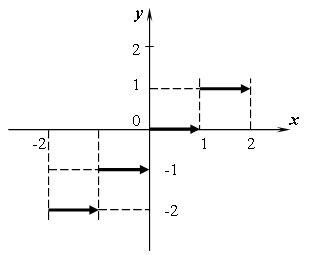
Словесным способом задаются специальные функции. Например, функция Дирихле функция сигнум (знакх) Эту функциюможно описать играфическим способом (рис. 11.2).

Рис. 11.2.

Графический способ состоит в изображении графика функции – множества точек плоскости, абсциссы которых есть значения аргумента х, а ординаты – соответствующие им значения функции .

Функция «целая часть х» задается особой формулой: , где– антье (от фр.entire – целый), и графическим способом (рис. 11.3).

Рис. 11.3.

Табличный способ задаёт функцию таблицей, содержащей значения аргумента х и соответствующие значения функции , например, таблица логарифмов.

11.3. Основные характеристики функции.

Определение 11.5. Пусть функция определена на множестве Х и длятакже принадлежит множеству Х. Тогда функцияназываетсячётной, если выполняется условие инечётной, если . График чётной функции симметричен относительно оси ординат, график нечётной функции симметричен относительно начала координат.

 Пример 11.1. а) ,– чётные функции; б),– нечётные функции; в)– ни чётная, ни нечётная функция. 

Определение 11.6. Функция называетсявозрастающей (убывающей) на промежутке Х, если большему значению аргумента из этого промежутка соответствует большее (меньшее) значение функции.

Пусть и . Тогда функция возрастает на промежутке Х, если и убывает, если.

Если , то функция называетсянеубывающей, если –невозрастающей.

Все названные функции называются монотонными функциями.

Возрастающие и убывающие функции называются строго монотонными функциями.

Определение 11.7. Функция , определённая на множестве Х, называетсяограниченной на этом множестве, если существует положительное число С такое, что для любого справедливо неравенство.

 Пример 11.2. Функция ограничена на R, т.к.

. 

Геометрически ограниченность функции означает, что её график находится внутри некоторой горизонтальной полосы (рис. 11.4).

Рис. 11.4.

Определение 11.8. Функция называется периодической с периодом , если для любых х из области определения функции.

Определение 11.9. Точка называетсяточкой локального максимума функции ,, если существует интервал,, содержащийся в Х и такой, что для каждого х из этого интервала имеет место неравенство.

Точка называетсяточкой локального минимума функции ,, если существует интервал,, содержащийся в Х и такой, что для каждого х из этого интервала имеет место неравенство.

Точки локального минимума и локального максимума называются точками локального экстремума функции.

 Пример 11.3. Рассмотрим функцию .

Имеем: 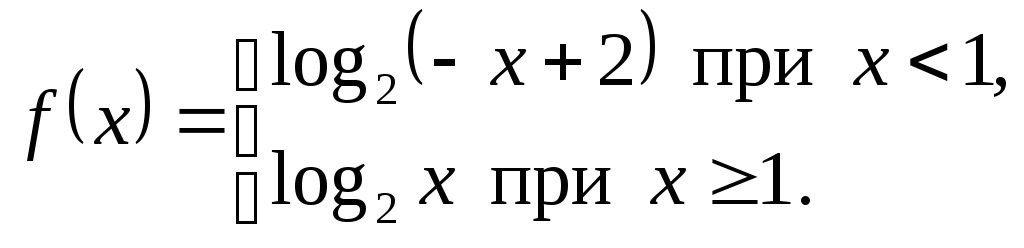Построим график (рис. 11.5).

Рис. 11.5.

Функция убывает наи возрастает на. В точкефункцияимеет локальный минимум.