

Атом водорода
Атом водорода — связанное состояние протона и электрона.
Vкулон =−e2
r
Спин протона |
s =12 |
Спин электрона |
sep =12 |
Энергии электрона атома водорода |
|
En = −13.6 |
n =1, 2, 3,... |
n2 |
|
Низший уровень n=1 соответствует основному состоянию. Чем больше n, тем дальше от ядра находится электрон и тем выше энергия уровня. Энергия состояния n=1, взятая с обратным знаком, представляет собой энергию ионизации – энергию, необходимую для отрыва от ядра электрона, находящегося в основном состоянии.
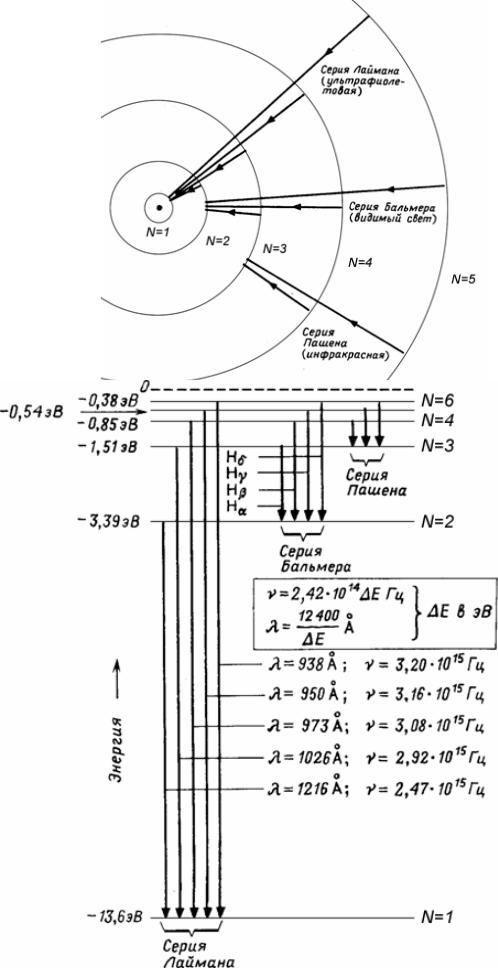
Атомводорода
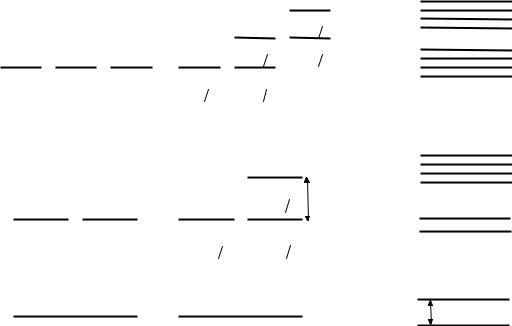
Схемауровнейатомаводорода
|
|
|
3d5 2 |
|
N =3 |
1,51 eV |
3p3 2 3d3 2 |
||
3s |
3p 3d |
3s1 2 3p1 2 |
||
|
||||
N = 2 |
3,4 eV |
|
2 p3 2 |
4,5 10−5 eV |
2s |
2 p |
2s1 2 2 p1 2 |
|
|
|
|
|||
|
13,6 eV |
|
0,6 10−5 eV |
|
N =1 |
|
λ = 21см |
||
1s |
|
1s1/ 2 |
||
|
|
в |
||
|
а |
|
б |
|
а– без учёта спина электрона и спина ядра,
б– тонкое расщепление уровней,
возникающее при учёте спина электрона, лембовское смещение уровней
2s1/2 – 2p1/2 составляет около 4*10-6 эВ,
а б в
в - сверхтонкое расщепление уровней, возникающее при учёте спина протона
Положения уровней и величины их расщеплений даны не в масштабе.
Атом водорода
Квантовые числа n (или N), l и m полностью характеризуют состояние электрона в атоме водорода, в рассмотренной нами упрощенной модели. Состояние с N
= 1 называется основным
состоянием атома водорода, так как в этом состоянии система обладает наименьшей энергией, и пребывает бòльшую часть времени. В атоме водорода энергия основного состояния E1 = −13.6 эВ. Состояния с N = 2, 3, … называются
возбужденными состояниями.
Энергия возбуждения Eвозб − это
энергия, которую необходимо сообщить системе, чтобы она перешла из начального состояния Ni в конечное состояние N f ,
определяется из соотношения
|
|
1 |
|
1 |
|
|
|
1 |
|
1 |
|
|
|
E = 2π |
сR |
− |
|
=13.6 |
|
− |
|
эВ |
|||||
2 |
2 |
2 |
2 |
||||||||||
возб |
|
|
|
|
|
|
|
|
|||||
|
Ni |
|
N f |
|
Ni |
|
N f |
|
|
||||
|
|
|
|
|
|||||||||
Пример.
Определить величину J полного момента количества движения электрона в состоянии 2p (N = 2, l = 1).
2p− электрон имеет
•Орбитальный момент l = 1. Величина орбитального момента
L = l(l +1) =  2
2
•Спиновый момент s = 1/2. Величина
спинового момента
S = |
1 |
|
1 |
|
= |
3 |
|
|
|
|
+1 |
|
|||
2 |
2 |
2 |
|||||
|
|
|
|
•Полный момент j = l + s = 1+ 1/2 = 3/2
или j = l − s = 1− 1/2 = 1/2.
Величина полного момента:
J = |
3 |
( |
3 |
+1) |
= |
15 |
|
2 |
2 |
2 |
|||||
|
|
|
|
или
J = |
1 |
( |
1 |
+1) = |
3 |
|
2 |
2 |
2 |
||||
|
|
|
Пример.
Рассчитать энергию перехода E между уровнями N=2 и N=3 (серия Бальмера) в атоме водорода.
|
1 |
|
1 |
|
|
|
E = −13.6 эВ |
|
− |
|
|
|
=1.9 эВ |
2 |
2 |
2 |
||||
|
3 |
|
|
|
|
|
Пример.
Рассчитать величину тонкого расщепления уровней 3p1/2, 3p3/2.
Величину тонкого расщепления уровней Е получим из соотношения:
E = 2π |
cR |
α2 |
1 |
||
|
|
|
|
||
N |
3 |
|
( j +1 / 2)( j + 3 / 2) |
||
|
|
|
|||
Для уровней 3p1/2, 3p3/2 ,N=3, J=1/2
Е = 1.3 10−5 эВ.
