
Угловое распределение вероятности
Для s-состояний угловая компонента волновой функции обладает сферической симметрией.
Для p-состояний (l=1) и
d-состояний (l=2) значения волновой функции в разных направлениях различны и зависят от абсолютного значения квантового числа m.
Частица в поле с центральной симметрией
2 |
|
d 2 |
|
|
2l(l +1) |
|
|
|||
− |
|
|
|
|
[rRnl |
(r)]+ U(r) + |
|
|
|
[rRnl (r)]= E[rRnl (r)] |
2M dr |
2 |
2Mr |
2 |
|||||||
|
|
|
|
|
|
|
||||
ψ(r,θ,ϕ) = Rnl (r)Ylm(θ,ϕ)
|
2 |
|
1 ∂ |
2 |
∂ψ |
|
1 ∂ |
|
∂ψ |
|
1 ∂2ψ |
|
|
||||||
− |
|
|
|
|
|
r |
|
|
+ |
|
|
|
(sinθ |
|
) + |
|
|
|
+U (r)ψ = Eψ. |
|
|
|
|
r2 sinθ ∂θ |
∂θ |
r2 sin2θ ∂ϕ2 |
|||||||||||||
|
2M r2 ∂r |
|
∂r |
|
|
|
|
|
|||||||||||
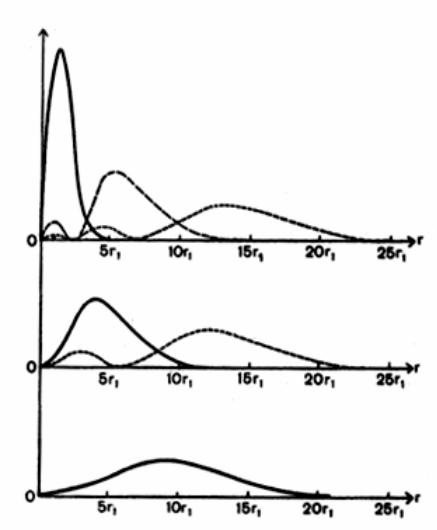
|Rnl(r)|2=r2dr
1s s-состояния
2s 3s
2p |
p-состояния |
|
3p |
3d d-состояниe
Радиальное распределение вероятности
r1 − радиус Бора (0.53Å)
Радиальноеквантовоечисло n
ψ(r,θ,ϕ) =Rnl (r)Ylm(θ,ϕ)
Радиальное квантовое число n описывает
поведение радиальной волновой функции Rnl (r) , определяющей энергию частицы в
заданном потенциале. Характер радиальной функции в первую очередь зависит от числа ее узлов, т. е. числа прохождения через нуль в интервале r от
нуля до бесконечности. Rnl (r) в случае
связанных (пространственно ограниченных) состояний асимптотически обращается в нуль на бесконечности. Обычно n считают равным числу узлов
функции Rnl (r) , в области r > 0, т. е.
исключают при их подсчете узел в начале координат, но при этом учитывают обязательный узел на бесконечности. Число n в формуле, описывающей
состояния частицы в прямоугольной яме, имеет тот же смысл.
|
|
Частица в поле |
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
с центральной симметрией |
||||||||||||||||||||||||||||
R (r) = e−nr rl L (r) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
nl |
|
nl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L (r) = A + A r + A r |
2 +...+ A |
|
−l−1 |
rn−l−1 |
|||||||||||||||||||||||||
nl |
0 |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
n |
|
|
|
|
||||||||
Lnl (r) −присоединённые полиномы Лагерра |
|||||||||||||||||||||||||||||
|
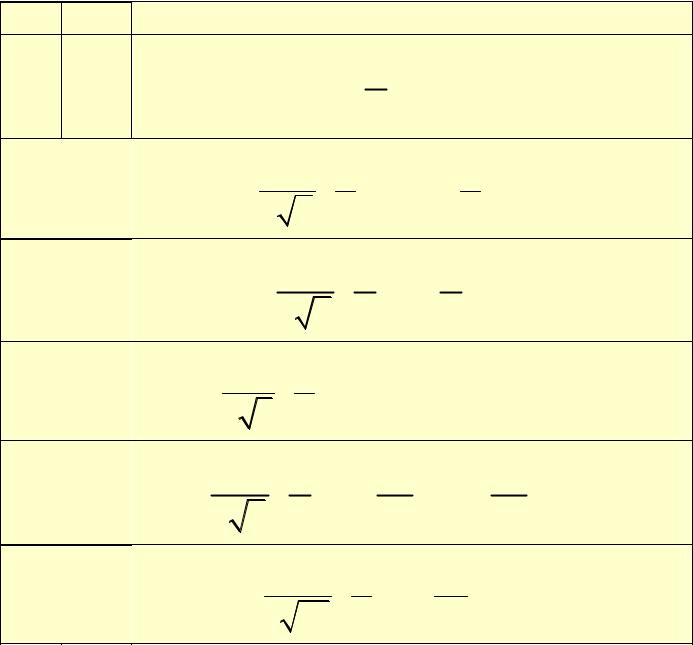
Первые нормированные радиальные функции Rnl |
||||||||||||||||||||||||||||
n |
l |
|
|
|
|
|
|
|
|
|
|
Rnl |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1 |
0 |
|
|
|
|
|
1 |
|
3/ 2 |
|
|
−r / r1 |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
2 |
0 |
|
1 |
|
1 |
|
3/ 2 |
|
|
2 |
− |
r |
|
|
|
|
−r / 2r1 |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|||||||||||
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
r1 |
|
|
|
|
|
||||||||||
2 |
1 |
|
|
1 |
|
|
|
1 |
|
3/ 2 |
r |
|
|
|
|
|
−r / 2r1 |
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
e |
|
|
|
|
|
|
|||||
|
|
|
|
6 r1 |
|
|
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||||
3 |
0 |
1 |
|
1 |
|
3/ 2 |
|
6 − |
|
4r |
|
+ |
4r2 |
−r / 3r1 |
|||||||||||||||
|
|
|
|
|
|||||||||||||||||||||||||
|
|
9 3 |
|
|
|
|
|
|
r1 |
|
|
|
|
|
|
|
e |
|
|
||||||||||
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
9r1 |
|
|
||||||||||||||
3 |
1 |
1 |
1 |
|
3/ 2 |
|
2r |
|
|
|
|
|
|
|
2r |
|
−r / 3r1 |
||||||||||||
|
|
|
|
4 |
− |
|
|||||||||||||||||||||||
|
|
9 6 |
|
|
|
|
|
|
3r1 |
|
|
|
|
|
e |
|
|||||||||||||
|
|
r1 |
|
|
|
|
|
|
|
|
3r1 |
|
|
||||||||||||||||
3 |
2 |
|
1 |
|
|
1 |
|
|
3/ 2 |
|
|
2r |
|
2 |
|
e |
−r / 3r1 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
9 30 |
|
|
|
|
|
|
|
|
|
3r1 |
|
|
|
|
|
|
|
||||||||||
|
|
r1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
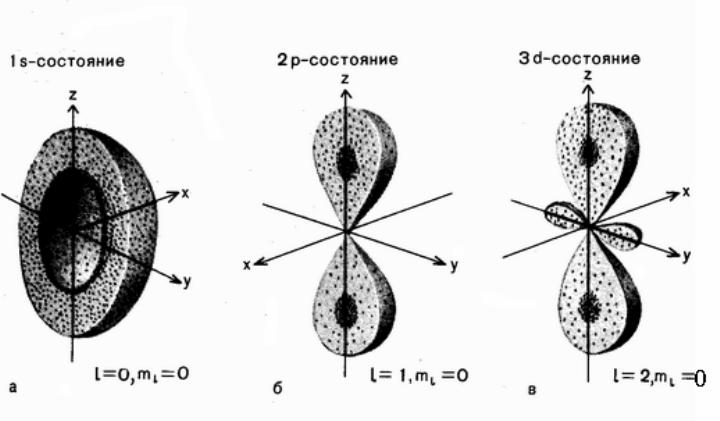
Распределение полной вероятности
Распределение полной вероятности
|Rnl (r) Ylm (θ,ϕ) |2r2drdΩ нахождения электрона в
атоме водорода, определяемое угловой и радиальной плотностью вероятности.
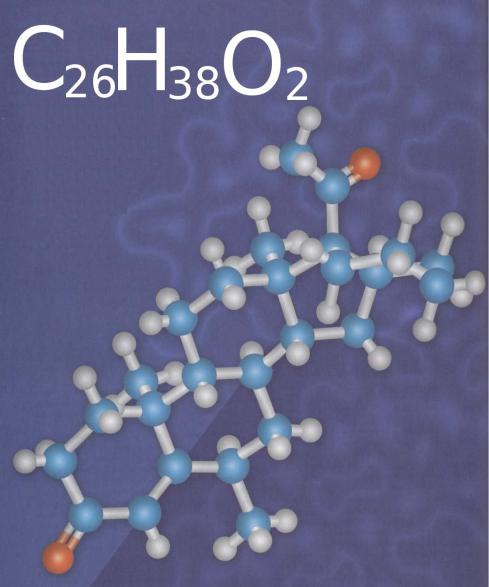
При переходе от атомов к молекулам квантовые свойства образующихся структур сохраняются. Химические и физические свойства молекул определяются относительно слабо связанными внешними электронами атомов, образующих молекулы. Равновесная пространственная конфигурация молекулы определяется минимумом потенциальной энергии взаимодействующих атомов. Равновесная конфигурация молекулы может обладать определённой симметрией, характеризуемой, например, наличием центра симметрии, плоскостей симметрии, осей симметрии и других типов симметрии.
Частицывполе
сцентральнойсимметрией
ψ(r,θ,ϕ) = Rnl (r)Ylm (θ,ϕ)
Вполе с центральной симметрией сохраняются:
E – энергия,
2l(l +1) - квадрат орбитального момента
m - проекция орбитального момента
E, l, m.
Состояние частицы, находящейся в сферически симметричном поле, полностью описывается тремя квантовыми числами: n, l и m При этом предполагается, что частица не имеет внутреннего углового момента, то есть спин S частицы равен 0.
n =1,2,3...
l = 0,1,2,3...
m = 0,±1,±2... ±l

Спиновой
моментчастицы
Спин — собственный момент количества движения частицы. Спин был первоначально введен для того, чтобы объяснить тот экспериментально наблюдаемый факт, что многие спектральные линии в атомных спектрах состоят из двух близко расположенных линий.
Спин имеет квантовую природу и не связан с какими-либо перемещениями частицы в пространстве. Спин измеряется в единицах постоянной Планка и равен s — характерное для каждой частицы полуцелое или целое (включая
нуль) положительное число
S 2 = 2s(s +1)
Спин частиц может иметь только дискретный набор значений. Это одна из характерных особенностей квантовой физики.
Спин
Спиновое квантовое число s может быть как целым (включая нуль), так и полуцелым, т. е. 0, 1/2, 1, 3/2, 2, 5/2, … , но при этом для каждой элементарной частицы он может принимать единственное присущее этому типу частиц значение. Так, спины π-мезона и К-мезона равны 0.
Спины электрона, протона, нейтрино, кварков и их античастиц равны 1/2. Спин фотона равен 1. Спин частицы невозможно изменить, также как её заряд или массу. Это её неизменная квантовая
характеристика. Проекция sz вектора спина S на
любое фиксированное направление в пространстве (например, на ось z) может принимать 2s + 1 значение:
sz |
= ±s , ±(s −1) , |
|
± (s − 2) , ..., ±1 / 2 (или 0) . |
Число |
sz − это квантовое число проекции спина. |
Максимальная величина sz совпадает с s. Так как
спин электрона равен 1/2, то проекция спина
может принимать лишь два значения sz = ±1/2. Если проекция +1/2, то говорят, что спин направлен вверх, если проекция −1/2, то говорят, что спин
направлен вниз.
Полныймомент количествадвижения (1)
В классической физике полный момент количества движения частицы или системы частиц является непрерывной величиной. Полный момент количества движения является вектором, и должен быть задан тремя его проекциями Jx, Jy, Jz. Полный момент количества движения частицы складывается из его орбитального момента
L =r ×p и спинового момента S :
J =L+S |
(*) |
|
Вквантовой теории ситуация аналогичная. Полный момент количества движения также описывается соотношением, аналогичным (*), в котором величины J, L и S заменены на операторы полного момента Jˆ , орбитального момента Lˆ и спинового момента Sˆ .
Всоответствии с общими правилами для квантовых векторов проекция полного момента на выделенную ось (z) может
+1 значение:принимать 2j
jz = ± j , ±( j −1) , ±( j − 2) , ..., ±1 / 2 (или 0)
Квантовые вектора (соответствующие им квантовые числа l, s и j) не могут принимать непрерывный ряд значений, а всегда обязаны быть либо целыми (возможен и нуль), либо полуцелыми числами.
Полныймомент количествадвижения (1)
Следствием этого является правило сложения квантовых векторов
|l − s| ≤ j ≤ l + s,
Левая часть этого неравенства соответствует минимальному значению вектора , когда вектора l и s направлены в противоположные стороны.
Правая часть неравенства отвечает максимальному , когда l и s направлены в одну
сторону. С учетом требований пространственного квантования все возможные j заключены в интервале от |l − s| до l + s и изменяются в пределах
этого интервала с шагом 1.
Для проекций jz ,lz , sz существует простое |
|
алгебраическое соотношение |
. |
jz =lz + sz |
(**) |
Из соотношения (**) вытекает очевидное следствие: если спин частицы целый (или нуль), то полный момент j также целый (или нуль); если же спин полуцелый, то полный момент обязательно полуцелый.
Пример
Сложениеспиновогои
орбитальногомоментов
J = l + s
l = 2 |
s = |
1 |
||
|
|
|
|
2 |
J = l + s = |
3 |
, |
5 . |
|
|
2 |
|
2 |
|
Пример
Сложениемоментов
J = J1 + J2
J1 + J2 ≥ J ≥| J1 − J2 |
J1 = 2 J2 = 3
J =1, 2,3, 4,5.
Квантовые состояния
ψ(x, y, z) = Rnl (r)Ylm (θ,ϕ)
| nlj >
n - номер состояния с данным l l - орбитальный момент
j - полный момент j = l + s s - спин
1 d5/2 |
E, Jp |
|
|
Связанные состояния в |
n |
|
центрально-симметричном поле |
|
l |
описываются определённым |
|
набором квантовых чисел. |
|
|
|
jn определяет уровни энергии связанных состояний частицы.
АтомБора… Квантоваятеория
В 1913 году Н. Бор предложил квантовую теорию орбит. Согласно этой теории электрон может вращаться вокруг ядра неопределенно долго, не излучая энергию, если на его орбите укладывается целое число длин волн де Бройля. Таким образом, устойчивые орбиты в атоме это орбиты,
радиусы |
которых |
rn |
определяются |
||
соотношением |
|
|
|||
|
|
|
r = n2 2 / Zm e2 |
|
|
|
|
|
n |
e |
|
что |
соответствует |
|
определенным |
||
энергетическим уровням атома. |
|||||
|
E |
n |
= −Z 2e4 m / 2n2 2 |
||
|
|
|
e |
|
|
Атом может перейти из одного состояния в другое, испустив квант энергии — фотон
ω = Ei − Ek
где Ei и Ek – энергии уровней, между которыми происходит переход.
Модель Бора не объясняла, почему, находясь на устойчивой орбите, электрон не излучает энергию? Почему переходы происходят именно между этими дискретными уровнями? И на ряд других вопросов.
