
Пример
Рассчитать расстояние между уровнями 1s, 2s и 3s ядра 90Zr для прямоугольной потенциальной ямы бесконечной глубины и ямы гармонического осциллятора.
В прямоугольной яме энергии уровней с l = 0
определяются соотношением En = (2nmRπ)22 ,
n — главное квантовое число, m — масса нуклона и R — радиус ядра (ширина ямы). Величина
расстояний между уровнями 1s, 2s и 3s будет
|
E |
|
= 3 |
(π |
)2 |
|
= 3 |
|
(π |
c)2 |
|
≈ |
|||||||||
|
|
2mR2 |
2mc2 |
(r A1/3 )2 |
|
||||||||||||||||
|
|
1s→2s |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
≈ |
|
|
3× |
(3,14×200)2 |
МэВ2 Фм2 |
|
|
= |
|||||||||||||
2 |
|
|
|
|
|
|
|
|
|
|
1/ 3 |
) |
2 |
Фм |
2 |
||||||
|
×931,5 МэВ×(1,2×90 |
|
|
|
|
|
|||||||||||||||
= 3×7,3 МэВ= 22 МэВ; |
|
|
|
|
|
|
|
|
|||||||||||||
|
|
E |
|
= |
5 |
(π |
)2 |
= 5 |
(π c)2 |
|
|
|
≈ |
||||||||
|
|
|
2mR2 |
2mc2 |
(r A1/3 )2 |
|
|||||||||||||||
|
|
|
2s→3s |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
≈5×7,3 МэВ= 36,5 МэВ.
Вяме гармонического осциллятора выражение для
энергии |
уровней |
с |
l = 0 |
определяется |
соотношением En = |
ω(2n +3/ 2), |
|
||
ω = 41A1/ 3 = 41×901/ 3 = 9,1 МэВ для 90Zr. Расстояние будет E1s→2s = E2s→3s = 2 ω =18,2 МэВ.
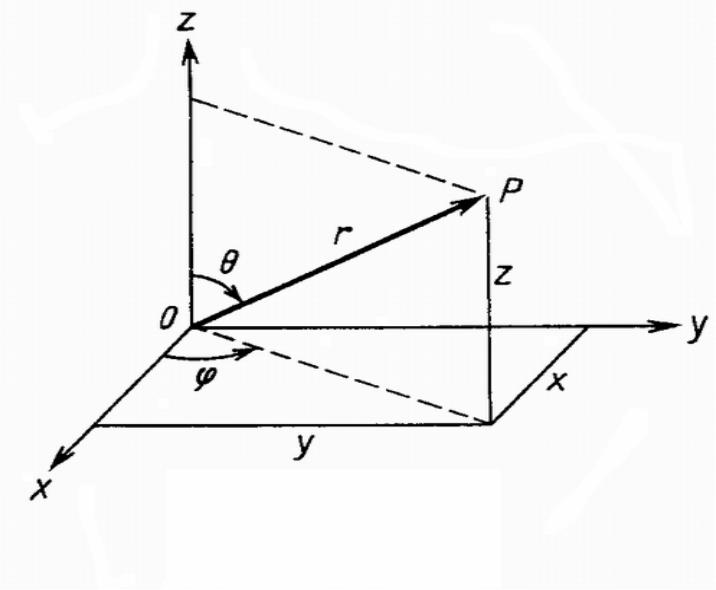
Прямоугольная и сферическая системы координат
x= r sinθ cosϕ,
y= r sinθ sinϕ,
z= r cosϕ.
Частицавполе
сцентральнойсимметрией
Стационарное уравнение Шредингера частицы в сферически симметричном потенциальном поле U(r)
|
2 |
|
1 ∂ |
∂ψ |
|
1 ∂ |
|
∂ψ |
|
1 ∂2ψ |
|
|
||||||
− |
|
|
|
|
|
r2 |
|
+ |
|
|
|
(sinθ |
|
) + |
|
|
|
+ |
|
|
|
r2 sinθ ∂θ |
∂θ |
r2 sin2θ ∂ϕ2 |
|||||||||||||
|
2M r2 ∂r |
∂r |
|
|
|
|
|
|||||||||||
+U(r)ψ =Eψ.
Волновая функция ψ(r,θ,ϕ) может быть представлена как произведение радиальной функции Rnl (r) и угловой
функции Ylm (θ,ϕ)
ψ(r,θ,ϕ) = Rnl (r)Ylm (θ,ϕ)
Уравнения для нахождения собственных значений и собственных функций угловой и радиальной функций.
|
2 |
1 |
|
∂ |
∂ |
|
1 ∂2 |
|
|
|
2l(l +1)Y (θ,ϕ) |
||||
− |
|
|
|
sinθ |
|
|
+ |
|
|
|
Y |
(θ,ϕ) = |
|||
|
|
|
sinθ ∂ϕ2 |
||||||||||||
|
|
sinθ |
∂θ |
∂θ |
|
|
lm |
|
lm |
||||||
2 |
|
d2 |
|
|
2l(l +1) |
|
|
|||
− |
|
|
|
|
[rRnl |
(r)]+ U(r) + |
|
|
|
[rRnl (r)]= E[rRnl (r)] |
2M dr |
2 |
2Mr |
2 |
|||||||
|
|
|
|
|
|
|
||||

Орбитальныймомент L Проекцияорбитальногомомента Lz
|
|
|
|
|
|
|
|
|
l = 0 |
|
s−состояние |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p−состояние |
|
|||||||
|
|
|
|
|
|
|
|
|
l = 1 |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
l = 2 |
|
d−состояние |
|
||||||||
|
|
|
|
|
|
|
|
|
l = 3 |
|
f−состояние |
|
||||||||
|
|
|
|
|
|
|
|
|
l = 4 |
|
g−состояние |
|
||||||||
|
|
|
|
|
|
|
|
|
l = 5 |
|
h−состояние |
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
и. т. д. |
|
|
|
|
|
|
|||
|
|
|
|
Оператор квадрата углового момента |
||||||||||||||||
2 |
|
2 |
|
1 ∂ |
|
|
|
∂ |
|
|
1 |
|
|
∂2 |
|
|||||
L |
= − |
|
|
|
|
|
|
|
(sin θ |
|
) + |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
∂θ |
sin |
2 |
θ |
|
∂ϕ |
2 |
||||||||
|
|
|
sin θ ∂θ |
|
|
|
|
|
|
|
|
|
||||||||
Уравнение для нахождения собственных значений и |
|
|
|
|||||||||||||||||
собственных функций оператора квадрата углового |
|
|
|
|||||||||||||||||
момента |
|
L2Y (θ,ϕ) |
= L2Y (θ,ϕ) |
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
lm |
|
|
lm |
|
|
|
|
|
|
|
|
|
|
|
||
Собственные значения оператора квадрата углового |
|
|
|
|||||||||||||||||
момента |
L2 = |
|
2l(l +1) |
|
|
l = 0, 1, 2, 3, …, |
|
|
|
|||||||||||
Уравнение для нахождения собственных значений и |
|
|
|
|||||||||||||||||
собственных функций оператора проекции углового |
|
|
|
|||||||||||||||||
момента |
|
Lz |
Ylm(θ,ϕ) |
= LzYlm(θ,ϕ) |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||
Собственные значения оператора проекции углового |
|
|
|
|||||||||||||||||
момента |
|
Lz |
= |
m |
|
|
m = 0, ±1, ±2... ±l |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||

Орбитальный момент количества
|
движения (1) |
ˆ |
||
|
|
|
ˆ2 |
|
Собственные значения операторов L |
и Lz |
|||
являются |
решением |
операторных |
||
уравнений |
|
|
|
|
ˆ2 |
2 |
Ylm |
(θ ,ϕ ) |
|
L Ylm |
(θ ,ϕ ) = L |
|
||
ˆ |
(θ,ϕ) = LzYlm(θ,ϕ) |
LzYlm |
Они имеют следующие дискретные значения
L2 |
= 2l(l +1) , где l = 0, 1, 2, 3,..., |
Lz = |
m , где m = 0, ±1, ± 2, ± 3,…, ± l . |
Сферические функции (их называют также сферическими гармониками) Ylm (θ ,ϕ)
являются |
собственными |
функциями |
||
операторов |
ˆ2 |
ˆ |
описывают |
|
L |
и Lz , т. е. |
|||
состояния с определенными l |
и m , а значит |
|||
и |
определенными |
значениями |
||
орбитального момента и его проекции на ось z . Сферические функции Ylm (θ ,ϕ) имеют
вид
Y (θ,ϕ) = (−1)m 2l +1 |
(l − |
|
m |
|
)! |
eimϕ Pm (cosθ ) |
, |
||
|
|
||||||||
|
|
||||||||
|
|
|
|
|
|||||
lm |
4π |
(l + |
m |
)! |
l |
||||
|
|
|
|||||||
Pl m (cosθ ) − функция Лежандра.

Орбитальный момент количества движения (2)
Для частицы, находящейся в сферически симметричном потенциале, величина орбитального момента количества движения L дается соотношением
L = l(l +1) .
Обычно, для упрощения, когда говорят о величине орбитального момента количества движения, называют этой величиной число l, имея в виду, что между l и L имеется однозначная связь
L = l(l +1) .
Так как величина l может принимать только целочисленные значения 0, 1, 2, 3,…, то и орбитальный момент количества движения квантуется. Например, для частицы с l = 2 момент количества
движения
L = 2(2 +1) = 6.58 10−22 6 МэВ с ≈ 2.6 10−34 Дж с.

Сферические функции
Сферические функции Ylm (θ , ϕ) удовлетворяют
уравнению
L2Y (θ,ϕ) = |
|
2l(l +1)Y (θ,ϕ), |
|
|
|
(*) |
|||||||||
|
lm |
1 |
|
∂ |
|
lm |
1 |
|
|
∂2 |
|
||||
|
|
|
|
∂ |
|
|
|||||||||
L2 |
=− 2 |
|
|
|
(sinθ |
|
)+ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
sinθ |
∂θ |
∂θ |
sin |
2 |
θ ∂ϕ |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|||||
l = 0, 1, 2, …; m = l, l−1, …, −l.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2l +1 (l − |
|
|
|
m |
|
|
)! |
ϕ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
Y (θ,ϕ) =(−1)m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
eim |
Pm |
(cosθ) |
|
|||||||||||||||||
|
|
|
4π |
|
|
(l + |
|
|
m |
|
|
|
|
|||||||||||||||||||||||||
|
lm |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
)! |
|
|
l |
|
|
|
|
|
|
||||||||||
Симметрия: |
|
|
|
|
Y |
(θ,ϕ)= (−1)mY |
(θ,ϕ). |
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
Ортогональность: |
lm |
|
|
|
|
|
|
|
|
|
|
|
|
l,−m |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
π |
|
|
|
|
|
2π |
Y |
(θ,ϕ)Y ′ ′(θ,ϕ)dϕ |
|
|
|
|
|
′δ |
|
|
||||||||||||||||||||||
∫ |
sinθdθ |
∫ |
=δ |
ll |
′ |
|
||||||||||||||||||||||||||||||||
0 |
|
|
|
|
|
|
0 |
|
lm |
|
|
|
|
|
|
|
l m |
|
|
|
|
|
mm |
|
||||||||||||||
Y |
= |
|
1 |
|
, |
Y |
|
= |
|
|
9 |
|
cosθ , Y |
=− |
|
3 |
|
|
sinθ eiϕ, |
|
||||||||||||||||||
4π |
|
|
|
4π |
|
8π |
|
|
||||||||||||||||||||||||||||||
00 |
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
iϕ |
|
||||||||||||||||||||
Y20 = |
5 |
|
3 |
|
|
2 |
θ − |
1 |
|
Y21=− |
|
15 |
|
|
|
|
|
|
, |
|||||||||||||||||||
4π |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
2cos |
|
2 |
, |
|
8π sinθcosθ e |
|||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
Y |
|
|
= |
|
|
|
15 |
sin2θ e2iϕ. |
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
32π |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
22 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Возможные значения орбитального квантового числа l
связаны со свойствами полинома Лежандра. Решение уравнения (*) существует только в том случае, когда
орбитальное квантовое число l имеет целочисленное
значение, включая 0. При этом оно должно быть больше абсолютного значения m или равно ему.

Орбитальный момент количества движения
Орбитальный момент количества движения является векторной величиной. Так как величина орбитального момента количества движения
квантуется, то и направление L по отношению к выделенному направлению z , например, к
внешнему магнитному полю, также квантуется (это называют пространственным квантованием) и принимает дискретные значения Lz = m, где m
изменяется от +l до −l , т. е. имеет 2l +1 значений. Например, при l = 2 величина m принимает значения +2, +1, 0, –1, –2. Энергия системы не
зависит от величины проекции орбитального
момента m, т. е. от направления вектора L , что
является очевидным следствием сферической симметрии системы.
Квантовые числа орбитального момента и его проекции
Появление квантовых чисел связано со свойствами симметрии системы. Характер этой симметрии диктует возможные значения квантовых чисел. Очевидно, что
система, описываемая функцией eimϕ ,
примет исходное значение только тогда, когда азимутальный угол ϕ в результате поворота вокруг оси z примет исходное
значение ϕ. Этому условию функция eimϕ
удовлетворяет только в случае, когда величина mϕ кратна 2π . Т.е. величина m
должна иметь целые значения. Так как необходимо учитывать вращение в двух
противоположных |
направлениях |
и |
||
отсутствие |
вращения, |
единственно |
||
возможными |
значениями |
оказываются |
||
m =0, ±1, ±2, … . |
|
|
|
|
Возможные |
значения |
орбитального |
||
квантового |
числа |
l |
связаны |
со |
свойствами полинома Лежандра. Решение уравнения существует только в том случае, когда l целое число, включая 0.
При этом оно должно быть больше абсолютного значения m или равно ему.

Угловое распределение вероятности
Распределение угловой вероятности Ylm (θ,ϕ) 2 dΩ
нахождения частицы в s-, p- и d-состояниях в сферически симметричном потенциале
