Масса атомного ядра
Основные методы определения масс ядер.
•Метод магнитного анализа. Магнитная жесткость Bρ , масса ядра M , его скорость V и заряд Q связаны соотношением
Bρ = MQV .
B - напряженность магнитного поля,
ρ- радиус поворота иона в магнитном поле.
•Метод времени пролета. Масса иона определяется из соотношения Bρ = MQ TL ,
T — время пролета расстояния L между детекторами.
•Измерение циклотронной частоты. Частота ω иона, вращающегося в постоянном магнитном поле B , связана с его массой M и зарядом Q соотношением ωB = MQ .
•Измерение энергии реакции Q .
В двухчастичной реакции A + a → B +b массы ядер связаны
соотношением M A + Ma = M B + Mb + cQ2 . Если известны
массы трех частиц, то масса четвертой частицы определяется по результатам измерения энергии реакции Q
•Измерение α-спектров. Для α-радиоактивных ядер масса
ядра определяется из анализа энергетических спектров α-частиц.
A → B +α, |
M |
A |
= M |
B |
+ M |
α |
+ |
Q |
, |
E = Q |
M B |
. |
|
|
|||||||||||
|
|
|
|
|
c2 |
|
α |
M A |
||||
|
|
|
|
|
|
|
|
|
|
|||
•Измерение энергии β -распада Qβ . Масса ядра, испытывающего β -распад, определяется из соотношения
A → B +e− (e+ ) +ν(ν), |
M |
|
= M |
|
+ m + |
Qβ |
. |
A |
B |
|
|||||
|
|
|
e |
c2 |
|||
|
|
|
|
|
|
||
Массаатомногоядра
Масса m и энергия покоя E частицы связаны соотношением
E = mc2 .
Когда протон и нейтрон соединяются в ядро дейтрон, происходит рождение γ -кванта с
энергией 2,2 МэВ.
p + n → d +γ (2,2 МэВ)
Т.е. энергия дейтрона на 2,2 МэВ меньше суммы энергий покоя протона и нейтрона. Следовательно, масса дейтрона меньше суммы масс протона и нейтрона на 2,2 МэВ/с2.
Зная величины mp , mn и md , можно
определить величину энергии выделяющейся при слиянии протона и нейтрона в дейтрон.
Источником энергии, выделяющейся на
Солнце, является образование ядра 4 He при
слиянии 4 протонов.
4 p → 4 He + 2e+ + 2νe
Масса ядра 4 He на 0,6% меньше массы
четырёх протонов. В результате синтеза 4 He
в процессе
4 p → 4 He + 2e+ + 2νe
выделяется энергия E ≈ 25 МэВ.
Энергиясвязи
ядра
Энергиясвязиядра W(A,Z)
Энергия связи ядра W(A,Z) – энергия, которую необходимо затратить для того, чтобы разделить атомное ядро на отдельные составляющие его нейтроны и протоны.
M(A, Z )c2 +W (A, Z ) =
=Z mpc2 +(A − Z )mnc2
Энергиясвязиядра
В таблицах свойств атомных ядер часто приводятся не массы атомных ядер M ядра , а
массы нейтральных атомов Mат . M ядра и Mат
связаны между собой соотношением
M ядра = Mат −Zme ,
Zme — полная масса электронов атома,
соответствующего данному ядру.
Энергией связи электронов с ядром можно пренебречь, т.к. она значительно меньше энергии связи нуклонов в ядре.
Формулу энергии связи ядра
W (A, Z ) = Zmp +( A − Z )mn c2 − M ядра ( A, Z )c2
можно переписать в виде
W ( A, Z ) = Z (mn −me )c2 −(A − Z )mnc2 −(Mат − Zme )c2
или
W ( A, Z ) = [Zmн + ( A − Z )mn ]с2 − M атc2 .
Атомнаяединицамассы. Дефектмассы
Атомная единица массы (а.е.м.) равна 1/12 массы атома углерода 12С.
1 а.е.м. =1,6582 10−24 г
или
931,44 МэВ.
Разность между массой ядра в атомных единицах массы и его массовым числом называется дефектом массы
= |
|
|
M |
|
|
− A. |
1 |
M ( |
12 |
|
|||
|
|
|
|
C) |
||
|
12 |
|
||||
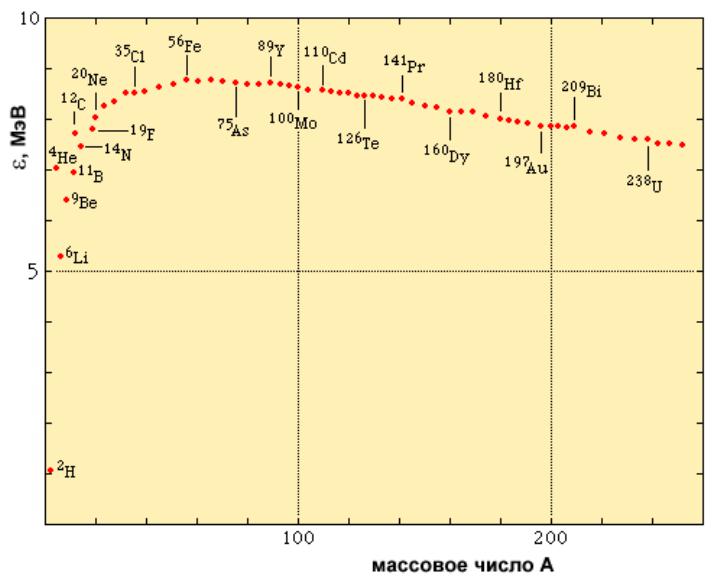
Удельная энергия связи ядра ε(A,Z)
Удельная энергия связи ядра ε (A,Z) – средняя энергия связи, приходящаяся на один нуклон.
ε(A, Z) = W(A, Z) A
Зависимость удельной энергии связи ε = W/A от
массового числа А