Характеристики ядерных состояний
Диаграмма уровней ядра строится следующим образом. Состояние с наибольшей энергией связи ядра, т. е. с наименьшей полной энергией Е, называют основным (ground state). Состояния с большей полной энергией – возбуждённые. Нижнему по энергии состоянию приписывается нулевой индекс и энергия
E0 = 0.
E0 → Mc2 = (Zmp + Nmn )c2 −W0 ,
W0 — энергия связи ядра в основном состоянии Энергии Ei (i =1, 2, …) возбуждённых состо-
яний отсчитываются от основного состояния. Нижние уровни ядра дискретны. При
увеличении энергии возбуждения среднее расстояние между уровнями уменьшается.
На схемах ядерных уровней обычно указывают энергию, спин и чётность каждого уровня. Спин указывается числом, а чётность знаком плюс для чётных и минус для нечётных уровней. Этот знак ставится справа сверху от числа, указывающего спин. Например, символ 1/2+ обозначает чётный уровень со спином 1/2, а символ 3− обозначает нечётный уровень со
спином 3.
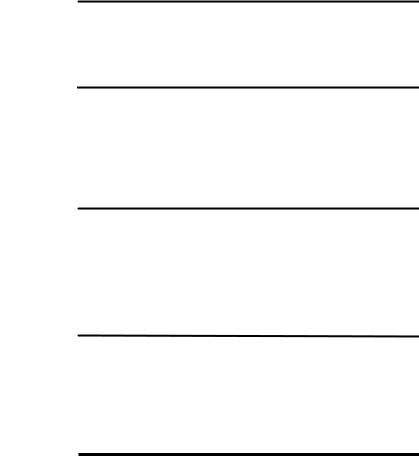
Пример. Характеристикиядерных состояний
МэВ
1,96
1,61
0,98
0,58
0,00
25Mg
5
2+
7
2+
3
2+
1
2+
5
2+
Схема нижних уровней ядра 1225Mg
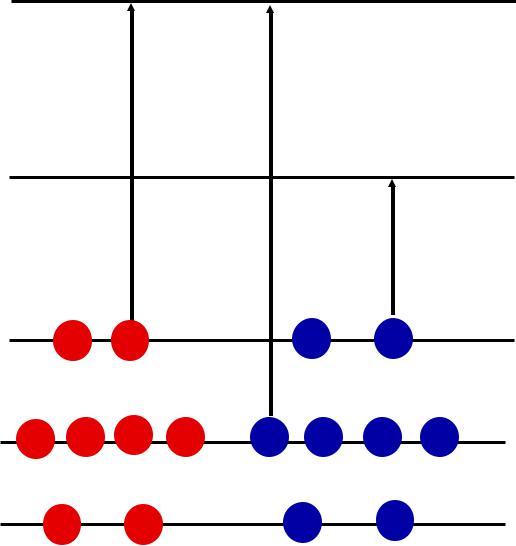
Одночастичные
возбужденияатомныхядер
Одночастичные возбуждённые состояния ядер возникают при переходе одного или нескольких нуклонов на более высокие одночастичные орбиты.
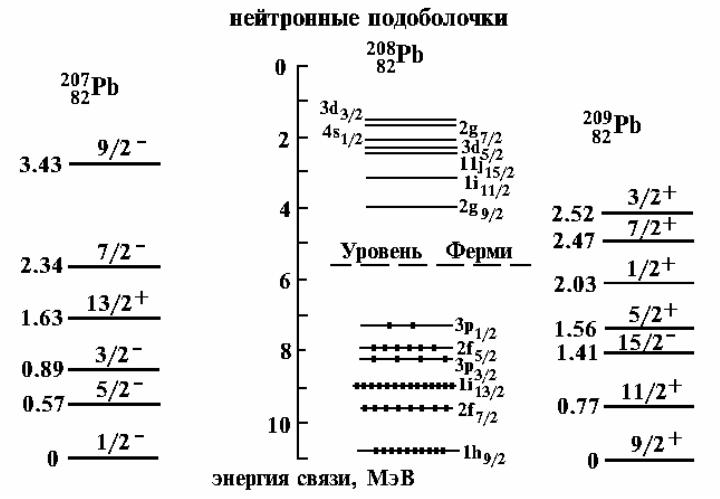
Одночастичныенейтронные
состояния
В одночастичной модели оболочек наиболее просто выглядит спектр возбуждённых состояний ядер с одним нуклоном или «дыркой» сверх заполненных оболочек. Нижние возбуждения такого ядра образуются перемещением этого внешнего нуклона на более высокие подоболочки ядра. Примерами возбуждений такого типа являются нижние возбужденные состояния ядер 20782 Pb и 20982 Pb.
Коллективные возбуждения атомных ядер
Ряд факторов свидетельствует о существовании коллективных степеней свободы ядер. Так, при малых энергиях возбуждения
Eвозб ≤ 4 МэВ у многих ядер
наблюдаются последовательности уровней, отвечающие гармоническим колебаниям ядерной поверхности, либо как вращательные полосы энергии, возникающие из-за вращения деформированного ядра как целого. Коллективная природа этих уровней подтверждается интенсивными квадрупольными электромагнитными переходами между ними, а также большой величиной квадрупольного момента ядер, имеющих постоянную деформацию.
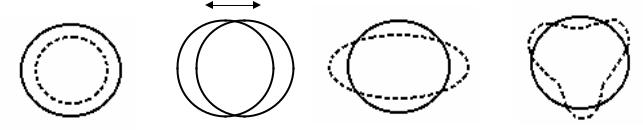
Колебательныесостояния
сферическихядер
J = 0 |
J = 1 |
J = 2 |
J = 3 |
монопольные дипольные квадрупольные октупольные
Примеры колебаний ядра как целого. Сплошной линией показана равновесная (сферическая) форма ядра, а пунктиром − одно из двух крайних
(различающихся половиной периода) состояний, которые принимает ядро в процессе колебаний. Дипольные колебания J=1 не относятся к внутренним возбуждениям ядра.
Энергии квадрупольных и октупольных возбуждений в квантовой теории могут принимать дискретные значения
Еквадр =n2 ω2 , Еокт = n3 ω3 ,
Энергия возбуждения ядра, в котором одновременно происходят различные поверхностные колебания формы, имеет вид
Е = ∑ n |
ω |
J |
J ≥2 J |
|
nJ − число фононов определенного типа, ωJ − энергия фонона.
Колебательныесостояния
сферическихядер
n = 3, Е = 3ћω2 |
0+,2+,3+,4+,6+ |
n = 2, E = 2ћω2 |
0+,2+,4+ |
n = 1, Е = 1ћω2 |
2+ |
n = 0, E = 0 |
0+ |
Спектр квадрупольных колебаний поверхности четно-четных ядер.
Пример.
Колебательныесостояниясферических
ядер
Взаимодействие γ-квантов с ядрами
Сечение фотопоглощения для четно-четных изотопов неодима.
В коллективной модели ядра гигантский резонанс описывается как дипольное колебание протонов относительно нейтронов. В деформированных ядрах с аксиальной симметрией гигантский дипольный резонанс расщепляется на две компоненты. Величина расщепления пропорциональна деформации ядра.
На рисунке экспериментальные сечения аппроксимируются сплошными линиями резонансных кривых Лоренца
σ = |
|
2 |
|
|
σ |
|
π |
|
Γ+ |
(E2 −E 2 )2 |
|
||
|
|
|
||||
|
|
|
|
E2Γ |
|
|
|
|
|
|
|
0 |
|
с параметрами, приведенными в таблице.
|
|
|
|
|
|
|
|
142Nd |
144Nd |
146Nd |
148Nd |
150Nd |
|
Е0, МэВ |
14.9 |
15.0 |
14.8 |
14.7 |
12.3 |
16 |
σ0, ферми2 |
36 |
32 |
31 |
26 |
17 |
22 |
Г, МэВ |
4.4 |
5.3 |
6 |
7.2 |
3.3 |
5.2 |
Сечение для ядра 150Nd аппроксимируется суммой двух резонансных кривых.