
- •Вопрос
- •Масса атомного ядра
- •Пример
- •Магические ядра
- •Пример
- •Зеркальные ядра
- •Пример
- •Пример
- •Пример
- •Вопрос
- •Вопрос
- •Спин-орбитальное взаимодействие
- •Пример
- •Вопрос
- •Пример
- •Пример
- •Характеристики ядерных состояний
- •Вопрос
- •Пример
- •Вопрос
- •Вопрос
- •Антиядра
- •Вопрос
- •Clustering building blocks: more than one nucleon bound, stable & no exited states below particle decay thresholds – 4He, deuterium, tritium, and 3He nuclei
Пример
На основании одночастичной модели оболочек определить значения спинов и
четностей J P основных состояний
изотопов кислорода — 15O, 16O, 17O, 18O.
Изотопы 16O и 18O четно-четные, то есть имеют в основном состоянии спин и
четность J P = 0+ . Спин и четность ядра
15O определяются «нейтронной дыркой» (по отношению к четно-четному ядру 16O)
в состоянии 1p1/ 2 . Спин ядра J равен
полному моменту «нейтронной дырки» в этом состоянии J =1/ 2, а четность определяется орбитальным моментом l
нуклона |
в |
данном |
состоянии |
P = (−1)l = (−1)1 = −1, то есть |
J P =1/ 2−. |
||
Спин и четность ядра 17O определяется |
|||
одним нейтроном в состоянии 1d5/ 2 сверх
четно-четного остова ядра 16O. Для ядра
17O J P = 5/ 2+ .
Магнитный
дипольный
моментядра

Магнитный дипольный
момент ядра
Величина магнитного дипольного момента ядра μ определяет его
энергию E взаимодействия с магнитным полем H .
Магнитный дипольный момент ядра имеет орбитальную и спиновую компоненты
μя = μ0 ∑A (glili + gsi si ) i=1
Магнитный момент протона
μp = +2,79μ0
Магнитный момент нейтрона
μn = −1,91μ0
μ0 = 2me pc = 3.15 10−18 ГауссМэВ
Магнитный дипольный момент ядра
E = −μH
μ = ∑A glli +∑A gs si μ0
gl |
1 |
p |
|
2 |
(2,79) |
p |
|
= |
n |
gs = |
(−1,91) |
n |
|||
|
0 |
|
2 |
||||
μ0 = |
e |
= 5 10−24 |
эрг |
= 3,15 10−18 |
МэВ |
||
2mp c |
Гаусс |
Гаусс |
|||||
|
|
|
|
||||
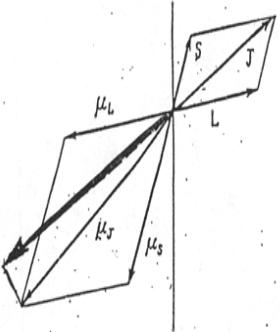
Среднее значение результирующего вектора μ = μl + μs из-за квантовых флюктуаций
имеет отличную от нуля составляющую μJ ,
направленную по направлению спина ядра J или против направления спина ядра J .
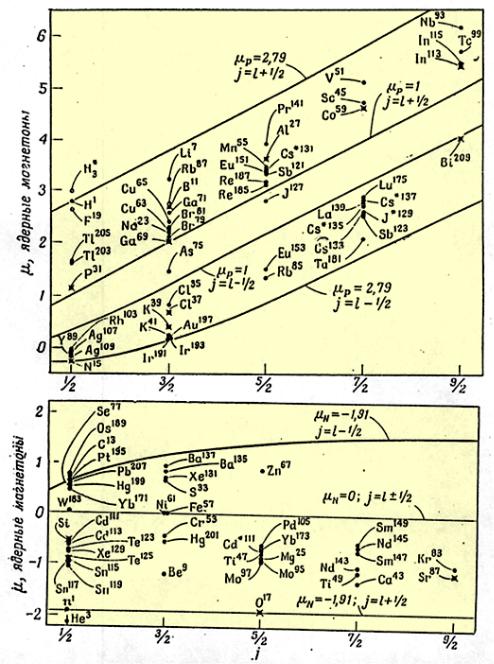
Магнитныемоментыядер
|
|
|
Нечётное Z |
|
|
|
|
Нечётное N |
||||||
j = l + |
1 |
μ = j − |
1 |
+ μp |
|
|
|
μn |
|
|||||
2 |
2 |
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
j = l − |
|
1 |
μ = j + |
|
j |
|
1 |
|
|
j |
|
|||
|
|
|
|
|
|
|
|
− μp |
− |
|
|
μn |
||
|
2 |
j |
+1 |
|
2 |
j +1 |
||||||||
|
|
|
|
|
|
|
||||||||
В одночастичной модели ядра магнитный момент нечётных ядер обусловлен магнитным моментом неспаренной нечётной частицы.
Изоспин
атомныхядер

Изоспинатомныхядер
Полный изоспин A нуклонов
A
I =α∑=1 Iα .
Все состояния ядра имеют проекцию
изоспина I3 = Z −2 N .
В ядре A нуклонов, каждый из которых имеет изоспин I = 12 . Поэтому возможные
значения изоспина |
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Z − N |
|
≤ I ≤ |
A |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
|
|
|
|
|
|
|
|||
Минимальное |
значение |
I = |
|
I3 |
|
. |
|||||||
|
|
||||||||||||
Максимальное |
значение |
I равно |
|
A |
|
и |
|||||||
|
2 |
|
|
||||||||||
отвечает всем Iα , направленным в одну
сторону.
Опытным путём установлено, что энергия возбуждения ядерного состояния тем выше, чем больше значение изоспина. Поэтому
изоспин ядра в основном состоянии Igs
имеет минимальное значение
Igs = I3 = Z −2 N .
Аналоговыесостоянияядер
Изоспины основных состояний ядер 37Li, 47Be Igs = 1/2. Основные состояния этих ядер
образуют изодублет. Для того, чтобы из ядра 37Li (I3 = −1/2), находящегося в основном
состоянии, получить ядро 47Be (I3 = +1/2) в
основном состоянии, нужно совершить поворот в изопространстве, в результате которого один из нейтронов ядра лития превратится в протон. При таком повороте все остальные квантовые характеристики у преобразованного нейтрона (орбитальный момент, проекция спина, четность и др.) сохраняются и переходят к протону. Остальные нуклоны при этом преобразовании не изменяют свои квантовые характеристики. В итоге получается система из четырех
протонов и трех нейтронов – ядро 47Be в
которой все нуклоны остались в тех же индивидуальных состояниях, в которых они
были до поворота в ядре 37Li т. е. ядро
бериллия окажется в основном состоянии, как и ядро лития. То, что основные состояния бериллия и лития эквивалентны, доказывается одним и тем же значением спинов и четностей (3/2−) их основных
состояний.
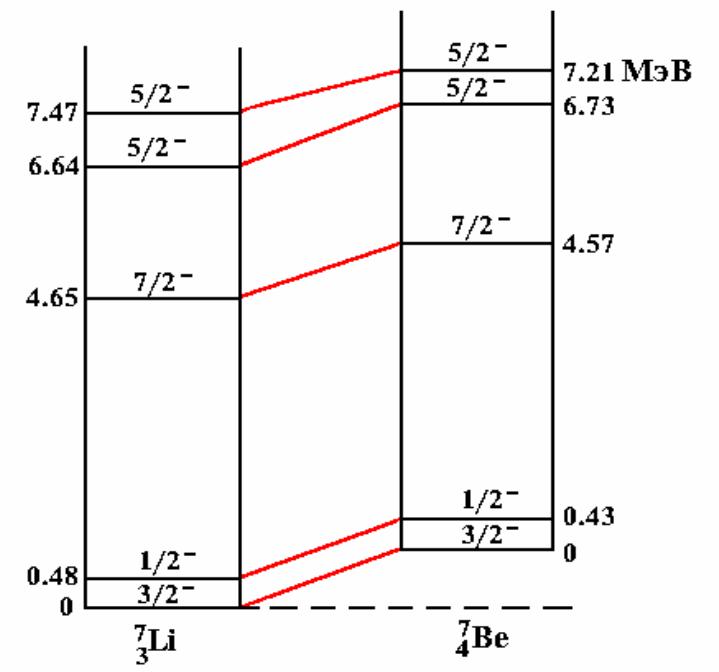
Аналоговые состояния ядер 7Li, 7Be
∆Е
Изодублеты (I = 1/2) уровней ядер 37Li и 47Be
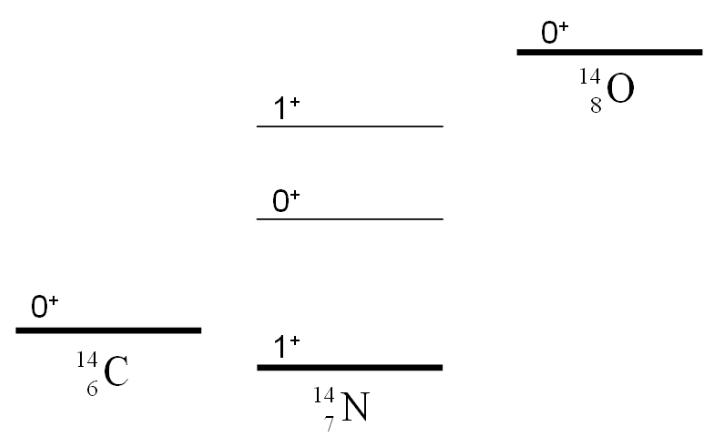
Аналоговыесостоянияядер
14С, 14N, 14O
0
2,31 МэВ
0
0
Зеркальные ядра являются частным случаем ядерных состояний, принадлежащих к одному изомультиплету. Примерами аналоговых состояний могут служить основные состояния ядер
14 C(6 p, 8n, J P = 0+ , T =1, T3 = −1) , 14 O(8 p, 6n, J P = 0+ , T =1, T3 = +1)
и |
первое |
возбужденное |
состояние |
ядра |
14 N(7 p, 7n, J P = 0+ , T =1, T = 0) |
с энергией 2,31 |
МэВ. |
||
|
|
3 |
|
|
Таким образом, в изомультиплет входят состояния с |
|||
одинаковыми значениями J P и T в соседних ядрах |
|||
изобарах. Так как проекция изоспина T3 принимает |
|||
2T +1 |
значение, |
изомультиплет |
образуют |
2T +1 ядерных уровней.

Пример
В ядре 90Zr (Z = 40) возбуждается состояние, имеющее изоспин I = 6. Показать, что распад
этого состояния в основное состояние ядра 89Zr с испусканием нейтрона невозможен.
Величины изоспинов основных состояний ядер
89Y и89Zr:
|
39 −50 |
|
|
11 |
|
|
|
|
40 − 49 |
|
|
9 . |
|
I(89Y) = |
|
|
= |
, |
I(89Zr) |
= |
|
|
= |
||||
|
2 |
|
2 |
2 |
|||||||||
|
|
|
|
|
|
|
|
|
|
2 |
|||
Величины изоспина протона и нейтрона
I(p) = I(n) = 12 .
Распады состояния I = 6 ядра 90Zr с испусканием
протона и нейтрона происходят в результате сильного взаимодействия. Поэтому из закона сохранения изоспина следует невозможность распада состояния ядра 90Zr I = 6 с испусканием
нейтрона
I(89 Y)+I(n)= 92 + 12 =4, 5 ≠6
