Добавил:

Upload Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Санкт-Петербургский государственный электротехнический университет "ЛЭТИ"

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Комплексные числа и многочлены

.pdf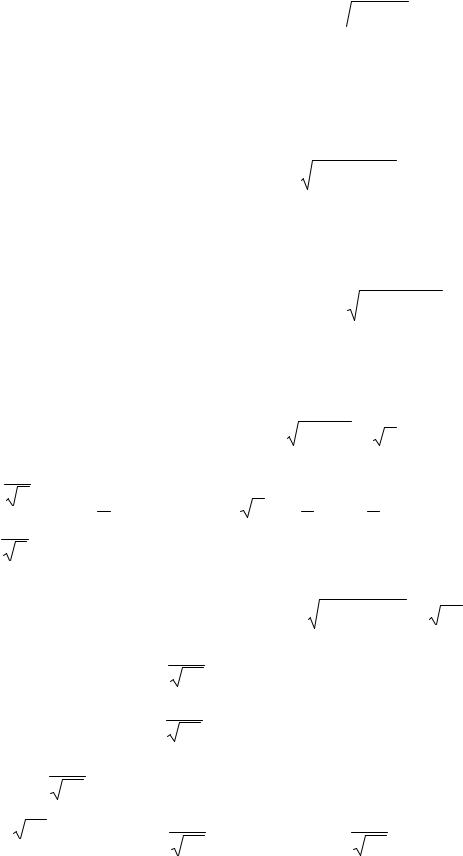

Скачиваний:

160

Добавлен:

18.04.2015

Размер:

527.62 Кб

Скачать

☆

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Для числа z = 1 a = 1, b = 0. Следовательно, ρ = 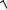12 +02 =1 и по формуле

(1.1) находим

cos ϕ =1,

Эта

система имеет решение: ϕ = 0 . В итоге:

sin ϕ = 0.

1 =cos0 +isin 0 .

Пример 15. Представить в тригонометрической форме число z = –i.

Для него a = 0, b = –1. Следовательно, ρ =

02 +(−1)2 =1 и система (1.1)

cosϕ = 0,

ϕ = −

. Отсюда −i = cos(−

) +i sin(−

) .

имеет вид:

ϕ = −1

sin

Пример 16. Представить в тригонометрической форме число z = –1.

Для числа z = –1 a = –1, b = 0. Следовательно, ρ =

(−1)2 +02 =1 и система

cosϕ

= −1,

ϕ = π. Получаем

−1 = cos π+i sin π.

(1.1) имеет вид

ϕ = 0

sin

Пример 17. Представить в тригонометрической форме число z = 1 + i.

Для него a = 1, b = 1. Следовательно,

ρ =

12 +12 =

2 и по системе (1.1)

cosϕ =

. Значит, 1+i =

2(cos

+i sin

) .

ϕ =

sin ϕ =

Пример 18. Представить в тригонометрической форме число z = –5 + 7i.

Для него a = –5, b = 7. Следовательно, ρ =

(−5)2 +72 = 74

и система

−5

cosϕ =

Решением этой системы будет

(1.1) принимает вид

sin ϕ =

7 .

ϕ = π−arccos

5 . Тогда

−5 +7i =

74(cos(π−arccos

) +i sin(π−arccos

)).

3.1.6. Умножение и деление комплексных чисел. Формула Муавра

Пусть z = ρ1(cos ϕ+i sin ϕ);

w = ρ2 (cos ψ +i sin ψ) . Тогда верны формулы:

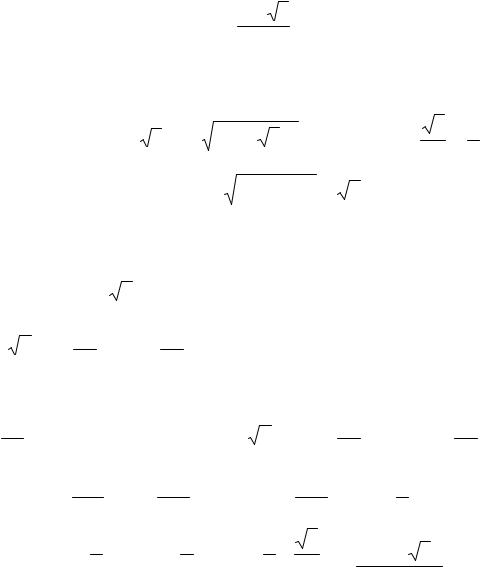
z w = ρ1 ρ2 (cos(ϕ+ψ) +isin(ϕ+ψ)) ,
	z	=	ρ1	(cos(ϕ−ψ) +isin(ϕ−ψ)),	(1.2)
	w
			ρ2
		zn = ρn (cos nϕ+isin nϕ) .			(1.3)

Последняя формула называется формулой Муавра [1, с. 190]. Она верна для любого натурального n.

	1+i	3	20

Пример 19. Вычислить:	1−i		.
	1−i

Решение. Переведем числитель и знаменатель дроби из алгебраической

формы в тригонометрическую.

Для числа z1

=1+i

3 ρ =

12 +( 3)2 = 2 , ϕ = arctg

3 =

π.

Для числа

z2 =1 −i

ρ = 12 +(−1)2 = 2 , ϕ = arctg

−1

= −

. Таким

образом,

2(cos

+isin 3)

=[поформуле(1.2)] =

2(cos(−

4) +isin(−

4))

=2(cos(127π) +isin(127π)).

Витоге:

2)20

(cos(7π 20) +i sin(7π 20)) =

=[по формуле(1.3)] = (

= 210

35π

(cos 3 +i sin 3

) =[так как

=12π−

] =

= 2

(cos(− 3) +i sin(−

3)) = 2

(2 −

i) = 2

− 3i).

3.1.7. Задачи на построение областей на комплексной плоскости

Пример 20. Изобразить на комплексной плоскости числа, модуль

которых равен 1, т. е.

=1.

Решение.

Запишем

комплексное

число

алгебраической

форме

z = x + yi . По

условию

задачи

интерес представляют те числа,

модуль

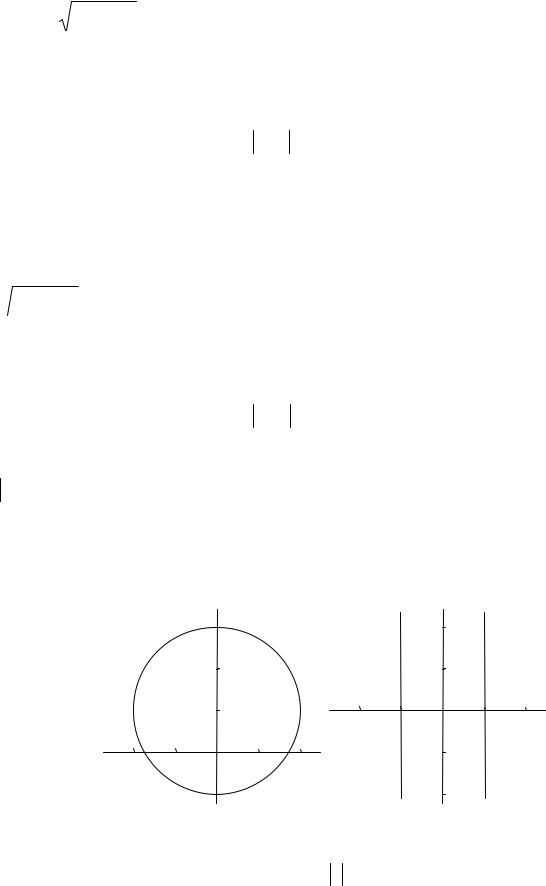
которых равен 1, т.		е.	x + yi	=1. По определению модуля комплексного

числа	x2 + y2 =1.	Возведя обе части равенства в квадрат, получим
x2 + y2 =1. Данное		уравнение определяет на плоскости окружность с

центром в точке с координатами (0; 0) и радиусом, равным 1.

Пример 21. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству z −i ≤ 2.

Запишем комплексное число в общем виде z = x + yi . По условию задачи, интерес представляют те числа, модуль которых меньше или равен 2,


т. е.	x + yi −i	≤ 2. Сгруппируем под знаком модуля слагаемые, содержащие
т. е.	x + yi −i	≤ 2. Сгруппируем под знаком модуля слагаемые, содержащие
i :	x +( y −1)i		≤ 2 . По определению модуля комплексного числа:
i :	x +( y −1)i		≤ 2 . По определению модуля комплексного числа:

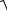x2 + y2 ≤ 2 x2 + y2 ≤ 4 .

Данное уравнение определяет на плоскости круг с центром в точке с координатами (0; 1) и радиусом равным 2 (рис. 1.3).

Пример 22. Найти геометрическое место точек, изображающих числа z, удовлетворяющие неравенству Re z <1.

Re z – действительная часть числа z, неравенство можно записать как

x	<1, или	x <1	или −1 < x <1. Эта система определяет на плоскости
x	<1, или		или −1 < x <1. Эта система определяет на плоскости
		x > −1
		x > −1

полосу, ограниченную прямыми x = 1 и x = -1. Причем, обе прямые нарисованы на штрихами, так как сами прямые в искомую область не входят из-за строгого знака неравенства (рис. 1.4).

	Y		Y
	3
	2		1
	1	-1	1	X
		-1	1	X
-1	1	X	-1
-1	-1	X
	-1
	Рис. 1.3		Рис. 1.4

Пример 23. Найти геометрическое место точек, изображающих числа z,

z ≤ 2,

удовлетворяющие системе неравенств

Re z >1.

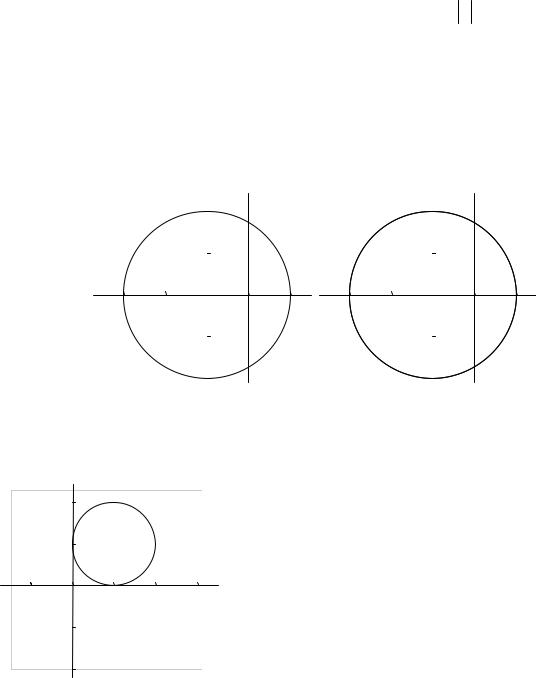
Как показано в примерах 20 и 21, неравенство z ≤ 2 определяет на

плоскости круг с центром в точке (0; 0) и радиусом, равным 2. Неравенство Re z >1, согласно примеру 22, определяет полуплоскость, ограниченную прямой x = 1 и находящуюся от нее справа. Так как неравенство Re z >1 строгое, то сама прямая x = 1 в область не входит и штрихами

пунктиром. Обе эти области изображены на рис. 1.5. Искомая область представляет собой пересечение двух данных областей (рис. 1.6).

			Y										Y
			Y										Y
			2										2
			1										1
	-2	-1			1			2 X	-2			-1		1		2 X
			-1										-1
			-2										-2

			Рис. 1.5									Рис. 1.6
	Пример 24. Найти геометрическое место точек, изображающих числа z,
	Y				удовлетворяющие системе неравенств
	Y				удовлетворяющие системе неравенств
	2						z −1−i			>1
	2						z −1−i			>1
											π.
						π
	1					π		≤ arg z ≤
					−	4		≤ arg z ≤			4
						4					4
-1	1	2	3	X			Неравенство						z −1−i		>1		определяет
-1	1	2	3	X			Неравенство						z −1−i		>1		определяет
	-1				область вне круга с центром в точке (1; 1)													и
	-2				радиусом				1. Так			как	неравенство				строгое,	то
					сама окружность в								область			не	входит	и

Рис. 1.7	изображена штрихами (рис. 1.7).

	Y			Y
	2			2
	1			1
-1	1 2	3 X	-1	1 2	3 X
	-1			-1
	-2			-2
	Рис. 1.8			Рис. 1.9

Двойное неравенство − π4 ≤ arg z ≤ π4 определяет на плоскости область, в

которую входят комплексные числа с аргументами в интервале от − π4 до π4 .

Эта область представляет собой угол (рис. 1.8).

Искомая область представляет собой пересечение двух данных областей

(рис. 1.9).

3.1.8.Извлечение корня из комплексных чисел в тригонометрической форме

Определения и утверждения к 3.1.8 можно найти в [1, с. 191-192]. Комплексное число w = n z называется корнем n-й степени из

комплексного числа z, если z = wn .

Утверждение. При любом натуральном n > 1 и любом комплексном z существует ровно n различных чисел wk , таких, что wn = z :

w = n ρ(cos ϕ+ 2πk		+isin ϕ+ 2πk ),	(1.4)
k	n	n

где k = 0, 1, 2, ..., n – 1.

Пример 25. Вычислить 4 −1 .

Решение. Для того чтобы воспользоваться формулой (1.4), необходимо представить число, стоящее под знаком корня, в тригонометрической форме.

Для числа z = -1 найдем его модуль и аргумент: ρ = 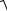(−1)2 +02 =1, ϕ = π. В

итоге −1 = cos π+isin π.

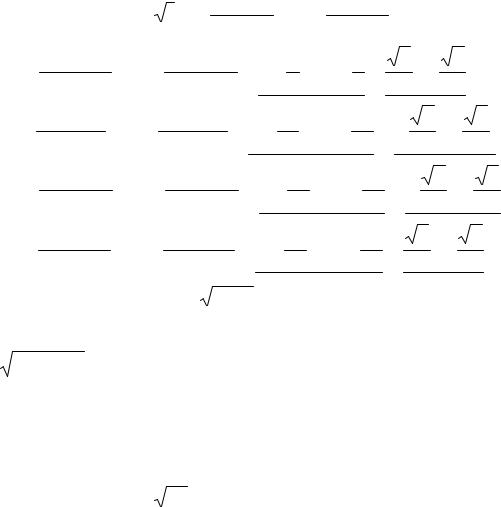
По формуле (1.4) w = 4	1(cos π+ 2πk	+isin π+ 2πk ) . Тогда:
k	4	4
	4	4

w	= cos π+ 2π 0 +isin π+ 2π 0 = cos π +isin π =																						2 +i				2 ,
0						4		4							4			4					2				2
						4		4							4			4					2				2
w	= cos π+ 2π 1 +isin π+ 2π 1 = cos 3π +isin 3π = −																									2 +i			2 ,
1						4		4							4			4								2			2
						4		4							4			4								2			2
w	= cos π+ 2π 2 +isin π+ 2π 2 = cos 5π +isin 5π = −																									2 −i				2 ,
2						4		4							4					4						2				2
						4		4							4					4						2				2
w	= cos π+ 2π 3 +isin π+ 2π 3 = cos 7π +isin 7π =																									2 −i			2.
3						4		4							4					4					2			2
						4		4							4					4					2			2
		Пример 26. Вычислить 5 −32i .
		Решение. Для числа z = −32i найдем его модуль ρ и аргумент ϕ:
ρ =		02 +322					= 32 , ϕ = − π, так как число z = −32i лежит на
								2																				−π					−π
отрицательной части мнимой оси. В итоге z = −32i = 32(cos																												−π			+i sin		−π		) .
отрицательной части мнимой оси. В итоге z = −32i = 32(cos																												2			+i sin				) .
													−π + 2πk						−π									2						2
													−π + 2πk						−π				+ 2πk
По формуле (1.4)								w = 5 32(cos					2				+isin			2							) ,
По формуле (1.4)								w = 5 32(cos									+isin										) ,
								k					5										5
где k = 0, 1, 2, 3, 4. Тогда:													5										5
где k = 0, 1, 2, 3, 4. Тогда:
w		= 2(cos				−π	+i sin		−π		),
w		= 2(cos					+i sin				),
0						10		10
						10		10
w	= 2(cos 3π +i sin 3π),
1				10				10
				10				10
w		= 2(cos 7π +i sin 7π),
2						10		10
						10		10
w	= 2(cos				11π		+i sin			11π		) = 2(cos		−9π	+i sin			−9π			),
w	= 2(cos						+i sin					) = 2(cos			+i sin						),
3						10		10					10					10
						10		10					10					10
w	= 2(cos15π						+isin15π ) = 2(cos −π +isin −π ).
4						10		10					2					2
						10		10					2					2
Для			w	и		w		аргументами					будут			−9π		и				−π		,		а	не				11π	и		15π
Для			w	и		w		аргументами					будут					и						,		а	не					и
		3					4								10								2							10				10
															10								2							10				10

соответственно, так как ϕ (−π; π].

	Пример 27. Вычислить 3 − 2 + 2													3i .
	Решение. Для числа							z = −2 + 2							3i		модуль ρ и аргумент ϕ есть:
ρ = (−2)2 +(2			3)2 = 4 +				124 = 16 = 4										, ϕ =	2π
																			.
																		3	.
В итоге z = −2 + 2 3i = 4(cos								2π			+i sin		2π			) . По формуле (1.4)
В итоге z = −2 + 2 3i = 4(cos							3				+i sin					) . По формуле (1.4)
							3							3
		2π		+2πk						2π		+2πk
				+2πk								+2πk
w	= 3 4(cos	3				+i sin			3						), где k = 0, 1, 2. Тогда:
w	= 3 4(cos					+i sin									), где k = 0, 1, 2. Тогда:
k			3				3
			3				3
w	= 3 4(cos 2π		+isin 2π),
0	9				9
	9				9
w	= 3 4(cos 2π		+isin 2π),
0	9				9
	9				9
w	= 3 4(cos 8π		+isin 8π),
1	9				9
	9				9
w	= 3 4(cos14π +isin14π) = 3 4(cos −4π +isin −4π).
2	9				9									9			9
	9				9									9			9

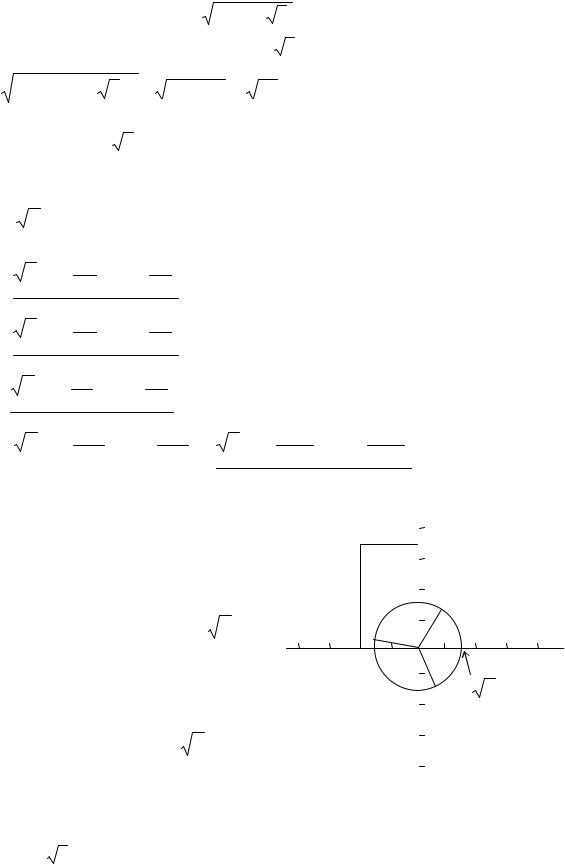
Из формулы (1.4) видно, что аргументы корней wk отличаются на одну и ту же

величину 2nπ , а модули всех

корней одинаковые и равны n ρ. Значит, на комплексной плоскости все wk лежат на окружности с центром в начале

координат	и		радиусом	n ρ	на
одинаковом		расстоянии		друг	от
друга.	Для		примера		27
изображения			самого	числа
z = −2 + 2	3i	и его корней w0 ,			w1 ,

	Im z
	.z
	.w3	.w1
	.w3	1 *2 3 4 Re z
	-4 -3 -2 -1	1 *2 3 4 Re z
		.w2 3 4

Рис. 1.10

w2 можно видеть на рис. 1.10.

2.МНОГОЧЛЕНЫ

2.1.Многочлены и действия над ними

Определения и утверждения к 2.1 можно найти в [1, с. 203-206].

Для действительной переменной x функция вида f (x) = axn , где a и x – действительные числа, а n – натуральное число или 0 (по-другому это можно записать как a R, n N {0}), называется одночленом с действительным коэффициентом.

Многочлен - это сумма одночленов, т.е. функция вида

g(x) = an xn + an−1xn−1	n
g(x) = an xn + an−1xn−1	+…+ a1x + a0 = ∑ai xi .
	i=0

При этом an называется старшим коэффициентом и an ≠ 0 , a0 - свободным членом, n - степенью многочлена.

Многочлен тождественно равен 0 тогда и только тогда, когда все его коэффициенты равны 0.

Если в записи многочлена нет какой-либо степени неизвестного, это значит, что коэффициент при этой степени равен 0.

На множестве многочленов определены следующие действия: 1. Сложение.

Пример 28. f (x) = 3x4 −7x2 + x −3; g(x) = 2x3 +5x2 +3x − 2 . Найти f (x) + g(x) .

f (x) + g(x) =3x4 + 2x3 +(−7 +5)x2 +(1+3)x +(−3 +(−2)) =

=3x4 + 2x3 −2x2 + 4x −5.

2.Умножение.

Пример 29. f (x) = 2x2 − x +1; g(x) = 3x −1. Найти f (x) g(x) . f (x) g(x) = (2x2 − x +1)(3x −1) =

=2x2 3x +(−x) 3x +1 3x + 2x2 (−1) +(−x) (−1) +1 (−1) =

=6x3 −3x2 +3x −2x2 + x −1 = 6x3 −5x2 + 4x −1.

3. Деление с остатком.
Разделить	f (x) на	g(x)	-	значит записать			f (x)	в виде
f (x) = g(x)q(x) + r(x),		или	f (x)	= q(x) +	r(x)	. Последняя		запись
f (x) = g(x)q(x) + r(x),		или	g(x)	= q(x) +	g(x)	. Последняя		запись
			g(x)		g(x)

аналогична записи для чисел: 173 = 5 + 23 , или 17 = 5 3 + 2.

Теорема (о делении с остатком) [1, с. 206]. Для любых многочленов

f (x)	и g(x) ≠ 0 существуют, и притом единственные,	многочлены q(x) и
r(x) , такие, что
	f (x) = g(x) q(x) + r(x) .	(2.1)
При	этом степень r(x) меньше степени g(x) , q(x) -	неполное частное,
r(x)	- остаток. Разделить f (x) на g(x) - значит записать	f (x) в виде (2.1).

Для практического нахождения частного и остатка существует метод деления «уголком».

Пример 30. Выполнить «уголком» деление с остатком: f (x) = x3 −3x2 − x −1 на g(x) = x2 − 2x +1.

Решение. Запишем делимое f (x) и делитель g(x) как при делении многозначных чисел:

x3 −3x2 − x −1 x2 − 2x +1

Находим частное от деления старшего члена делимого на старший член

делителя ( x3 / x2 = x ) и записываем результат в графу частного: x3 −3x2 − x −1 x2 − 2x +1

Умножаем делитель на результат деления и записываем под делимым:

x3 −3x2 − x −1 x2 − 2x +1
x3 − 2x2 + x	x

Вычитаем из делимого результат умножения:

x3 −3x2 − x −1			x2 − 2x +1

x3 −2x2 + x			x

− x2 − 2x −1

Проверяем степень получившегося в результате вычитания многочлена. Если она меньше степени делителя, то процесс деления закончен, и полученный многочлен является остатком. В противном случае деление продолжается аналогично описанному ранее:

x3 −3x2 − x −1 x2 − 2x +1
x3 − 2x2 + x	x - 1

−x2 − 2x −1

−x2 + 2x −1

-4x

Так как степень полученного многочлена меньше степени делителя, то процесс деления закончен. В результате: q(x) = x – 1– неполное частное, а

r(x) = –4x – остаток.

Ответ: x3 −3x2 − x −1 = (x2 −2x +1)(x −1) +(−4x) , или

x3 −3x2 − x −1		= x −1	−		4x	.

x2	−2x +1			x2	−2x +1

Пример 31. Выполнить деление с остатком: 3x5 +1 на x2 −1. Решение. Запишем делимое и делитель как при делении многозначных

чисел. Если в записи многочлена отсутствует одна или несколько степеней, то при записи, для удобства вычислений, следует на их места записать нули:

3x5 + 0x4 + 0x3 + 0x2 + 0x +1				x2 −1

3x5	−3x3			3x3 +3x

		3x3 + 0x2 + 0x
		3x3	−3x

3x +1

Получившиеся в результате умножения многочлены удобнее записывать, располагая слагаемые в соответствии с их степенями. Так как степень полученного многочлена меньше степени делителя, то процесс деления

закончен. В результате: q(x) =3x3 +3x – неполное частное, а r(x) = 3x + 1		–
остаток.
Ответ: 3x5 +1 = (x2 −1)(3x3 +3x) + (3x +1) , или 3x5 +1 = 3x3 +3x + 3x +1 .
x2 −1	x2 −1
Пример 32. Делится ли нацело многочлен	x4 + 4x3 − 2x −8 на
многочлен x3 − 2 ?

Решение. Разделим один многочлен на другой «уголком».

<<< < Предыдущая 12 / 42 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
09.02.20151.25 Mб24кельтская цивилизация.doc
#
22.04.20192.44 Mб60Кинематика криволинейного движения.docx
#
22.03.20169 Mб92Китайский рисунок кистью.pdf
#
16.11.2019482.71 Кб10КОЛЕБАНИЯ.docx
#
09.02.20151.3 Mб171Комплексные числа и многочлены.doc
#
18.04.2015527.62 Кб160Комплексные числа и многочлены.pdf
#
22.11.20191.13 Mб36компьютерные_технологии.doc
#
15.11.2018286.72 Кб8конденсатор.doc
#
09.02.20152.34 Mб8Конспек лекций по дисциплине.docx
#
22.03.20167.3 Mб28Конспект лекций.pdf
#
07.05.2019182.27 Кб2Конспект лекций2.doc