8. Декартова прямоугольная система координат в пространстве.

Три взаимно перпендикулярные оси в пространстве (координатные оси) с общим началом О и одинаковой масштабной единицей образуютдекартову прямоугольную (кратко -прямоугольную)систему координат в пространстве. Оси упорядочены, т.е. указано, какая из осей считается первой (она называется осью абсцисс и обозначается Ох), какая - второй (ось ординат Оу) и какая -третьей(ось аппликат Oz).

Различают  правую илевуюсистемы декартовых прямоугольных координат (рис. 36, соответственноа, б). В этой книге принята правая система координат (будем называть ееосновной.

Орты осей Ox, Oy, Oz обозначают соответственно. Так как векторыкомпланарны, то они образуют базис (см.п. 6), который называетсядекартовым прямоугольным базисом.

В силу результатов п. 6 каждый вектор может быть, и притом единственным способом, разложен по декартовому прямоугольному базису, т.е. для каждого вектора найдется, и притом единственная, тройка чисел, такая что справедливо равенство

Числа называются декартовыми прямоугольными( или прямоугольными)координатами вектора.

Рис.36

Запись () означает, что вектор: имеет декартовы прямоугольные координаты

Выясним геометрический смысл чисел . Используя теоремы 2 и 1 о проекциях (см. п. 7), имеем

Аналогично .

Следовательно, числа в формуле (7) являются проекциями вектора на координатные оси Ox, Oy,Oz соответственно.

Если М - произвольная точка в пространстве, то радиусом-вектором точки М назовем вектор, имеющий своим началом

начало О заданной системы координат, а концом эту точку.

Определение. Декартовыми прямоугольными координатами точки М называются проекции ее радиуса-векторана соответствующие координатные оси; проекция на первую координатную ось называется абсциссой точки М, на вторую - , на третью -аппликатой:

x = , у =, z =. СимволМ(х; у; z)означает, что точка М имеет координатых, у, z.

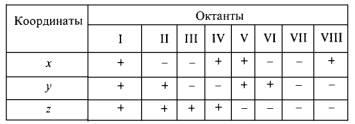
Координатные плоскости(плоскости, проходящие через пары координатных осей) делят все пространство на восемь частей, называемыхоктантами, которые нумеруются следующим образом: октант, лежащий над первой четвертью плоскостихОу, - I; лежащий под ней - V; соответственно октанты, лежащие над и под второй четвертью плоскостихОу, - II и VI; над и под третьей четвертью - III и VII; над и под четвертой четвертью - IV и VIII.

Каждому октанту соответствует определенная комбинация знаков координат:

Отметим, что каждой точке пространства соответствует одна упорядоченная тройка действительных чисел (х; у; z)(ее координат). Верно и обратное: каждой упорядоченной тройке действительных чисел(х; у; z) соответствует одна точка пространства. Это означает, что в пространстве положение произвольной точкиМ полностью определяется ее координатамих; у; z.имеем=(Если точка М лежит в плоскости хОу, то =)

Пусть заданы две точки М₁(х₁ ; у₁; z₁) и М₂(х₂; у₂; z₂).

Рассмотрим вектор .

Имеем =(рис. 37). Отсюда в силу теоремы 2 (см. п.6) получаем( х₂- х₁ ; у₂- у₁; z₂- z₁ ).

Итак, чтобы найти координаты некоторого вектора, достаточно из координат его конца вычесть одноименные координаты его начала.

Пусть два ненулевых вектора

коллинеарны. В этом случае (см. п. 2) =(- скаляр), что в силу следствия 2 из п. 7 равносильно трем равенствам

Это есть условие коллинеарности векторов.

Таким образом, векторы коллинеарны тогда и только тогда, когда их одноименные координаты пропорциональны.

Примечание. В равенстве (8) некоторые из знаменателей могут оказаться равными нулю. Напомним, что всякую пропорцию

понимаем в смысле равенства ad = be.

Так, например, равенства

Означают, что

.