6.Гравитационное поле, потенциальная энергия гравитационного поля

Гравитацио́нное по́ле - физическое поле, через которое осуществляетсягравитационное взаимодействие

В рамках классической физикигравитационное взаимодействиеописывается «законом всемирного тяготения»Ньютона, согласно которому сила гравитационного притяжения между двумя материальными точками с массамиm₁ и m₂ пропорциональна обеим массам и обратно пропорциональна квадрату расстояния между ними:

Здесь G — гравитационная постоянная, приблизительно равнаям³/(кг с²),R — расстояние между точками.

Потенциальная энергиячастицы вгравитационном полеравна еемассе, умноженной на потенциал поля. Дляпотенциальной энергиилюбого распределениямасссправедливо выражение:

где μ — плотность массытела,— гравитационный потенциал,V— объём тела.

Гравитационная энергия—потенциальная энергиясистемы тел (частиц), обусловленная их взаимнымтяготением.

Общепринята шкала, согласно которой для любой системы тел, находящихся на конечных расстояниях, гравитационная энергияотрицательна, а для бесконечно удалённых, то есть длягравитационноне взаимодействующих тел, гравитационную энергия равнанулю. Полная энергия системы, равная сумме гравитационной икинетической энергиипостоянна, для изолированной системы гравитационная энергия являетсяэнергией связи. Системы с положительной полной энергией не могут быть стационарными.

Для двух тяготеющих точечных тел с массами Mиmгравитационная энергияU_gравна:

,где:- гравитационная постоянная;-расстояние между центрами масс тел.

Этот результат получается из закона тяготения Ньютона, при условии, что для бесконечно удалённых тел гравитационная энергия равна 0. Выражение для гравитационной силы имеет видгде:F_g— сила гравитационного взаимодействия

С другой стороны согласно определению потенциальной энергии:

Тогда: ,

Константа в этом выражении может быть выбрана произвольно. Её обычно выбирают равной нулю, чтобы при r, стремящемуся к бесконечности, U_gстремилось к нулю.

Этот же результат верен для малого тела, находящегося вблизи поверхности большого. В этом случае R можно считать равным h+R_M, гдеR_M— радиус тела массой M, а h — расстояние от центра тяжести тела массой m до поверхности тела массой M.

На поверхности тела M имеем:

,

Если размеры тела Mмного больше размеров телаm, то формулу гравитационной энергии можно переписать в следующем виде:

,

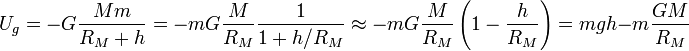где величину называют ускорением свободного падения. При этом членне зависит от высоты поднятия тела над поверхностью и может быть исключён из выражения путём выбора соответствующей константы. Таким образом для малого тела, находящегося на поверхности большого тела справедлива следующая формула

U_g=mgh

В частности, эта формула применяется для вычисления потенциальной энергии тел, находящихся вблизи поверхности Земли.

7.Центральный удар, абсолютно упругий и абсолютно неупругий удар

Уда́р- толчок, кратковременноевзаимодействиетел, при котором происходит перераспределениекинетической энергии. Часто носит разрушительный для взаимодействующих тел характер. В физике под ударом понимают такой тип взаимодействия движущихся тел, при котором временем взаимодействия можно пренебречь.

Абсолютно упругий удар - модель соударения, при которой полная кинетическая энергия системы сохраняется. В классической механике при этом пренебрегают деформациями тел. Соответственно, считается, что энергия на деформации не теряется, а взаимодействие распространяется по всему телу мгновенно. Хорошей моделью абсолютно упругого удара является столкновение бильярдных шаров или упругих мячиков.

В общем случае массы m₁и m₂соударяющихся шаров могут быть неодинаковыми. По закону сохранения механической энергии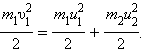

m1υ1= m1u1+ m2u2.

Здесь υ₁– скорость первого шара до столкновения, скорость второго шара υ₂= 0, u₁и u₂– скорости шаров после столкновения. Закон сохранения импульса для проекций скоростей на координатную ось, направленную по скорости движения первого шара до удара, записывается в виде:

Мы получили систему из двух уравнений. Эту систему можно решить и найти неизвестные скорости u₁и u₂шаров после столкновения: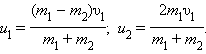

В частном случае, когда оба шара имеют одинаковые массы (m₁= m₂), первый шар после соударения останавливается (u₁= 0), а второй движется со скоростью u₂= υ₁, т. е. шары обмениваются скоростями (и, следовательно, импульсами).

Если бы до соударения второй шар также имел ненулевую скорость (υ₂≠ 0), то эту задачу можно было бы легко свести к предыдущей с помощью перехода в новую систему отсчета, которая движется равномерно и прямолинейно со скоростью υ₂относительно «неподвижной» системы. В этой системе второй шар до соударения покоится, а первый по закону сложения скоростей имеет скорость υ₁' = υ₁– υ₂. Определив по приведенным выше формулам скорости u₁и u₂шаров после соударения в новой системе, нужно сделать обратный переход к «неподвижной» системе.

Центральным ударомшаров называют соударение, при котором скорости шаров до и после удара направлены по линии центров.

Центральный (лобовой) удар очень редко реализуется на практике, особенно если речь идет о столкновениях атомов или молекул. При нецентральном упругом соударении скорости частиц (шаров) до и после столкновения не направлены по одной прямой.

Частным случаем нецентрального упругого удара может служить соударение двух бильярдных шаров одинаковой массы, один из которых до соударения был неподвижен, а скорость второго была направлена не по линии центров шаров .

После нецентрального соударения шары разлетаются под некоторым углом друг к другу. Для определения скоростейипосле удара нужно знать положение линии центров в момент удара или прицельное расстояние d , т. е. расстояние между двумя линиями, проведенными через центры шаров параллельно вектору скоростиналетающего шара. Если массы шаров одинаковы, то векторы скоростейишаров после упругого соударения всегда направлены перпендикулярно друг к другу. Это легко показать, применяя законы сохранения импульса и энергии. При m1= m2= m эти законы принимают вид:

Первое из этих равенств означает, что векторы скоростей ,иобразуют треугольник (диаграмма импульсов), а второе – что для этого треугольника справедлива теорема Пифагора, т. е. он прямоугольный. Угол между катетамииравен 90°.

Абсолю́тно неупру́гий удар— удар, в результате которого компоненты скоростей тел,нормальныеплощадке касания, становятся равными. Если удар был центральным (скорости были перпендикулярны касательной плоскости), то тела соединяются и продолжают дальнейшее своё движение как единое тело.

Примером абсолютно неупругого удара может служить попадание пули (или снаряда) в баллистический маятник. Маятник представляет собой ящик с песком массой M, подвешенный на веревках. Пуля массой m, летящая горизонтально со скоростью попадает в ящик и застревает в нем. По отклонению маятника можно определить скорость пули.

Обозначим скорость ящика с застрявшей в нем пулей через UТогда по закону сохранения импульса

При застревании пули в песке произошла потеря механической энергии:

Отношение M / (M + m) – доля кинетической энергии пули, перешедшая во внутреннюю энергию системы:

Эта формула применима не только к баллистическому маятнику, но и к любому неупругому соударению двух тел с разными массами.

При m << M почти вся кинетическая энергия пули переходит во внутреннюю энергию. При m = M– во внутреннюю энергию переходит половина первоначальной кинетической энергии. Наконец, при неупругом соударении движущегося тела большой массы с неподвижным телом малой массы (m >> М) отношение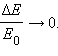

Дальнейшее движение маятника можно рассчитать с помощью закона сохранения механической энергии:

где h – максимальная высота подъема маятника. Из этих соотношений следует: