29.Электрическое поле на границе диэлектриков

Рассмотрим поведение векторов E и D на границе раздела двух однородных изотропных диэлектриков с проницаемостями ипри отсутствии на границе свободных зарядов.Граничные условия для нормальных составляющих векторов D и E следуют из теоремы Гаусса. Выделим вблизи границы раздела замкнутую поверхность в виде цилиндра, образующая которого перпендикулярна к границе раздела, а основания находятся на равном расстоянии от границы (рис. 2.6).

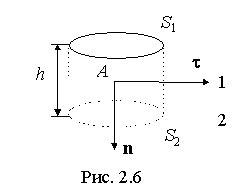
Так как на границе раздела диэлектриков нет свободных зарядов, то, в соответствии с теоремой Гаусса, поток вектора электрической индукции через данную поверхность: .

Выделяя потоки через основания и боковую поверхность цилиндра, где- значениекасательной составляющей усредненное по боковой поверхности. Переходя к пределу при(приэтом также стремится к нулю), получаем, или окончательно для нормальных составляющих вектора электрической индукции:.

Для нормальных составляющих вектора напряженности поля получим: .

Таким образом, при переходе через границу раздела диэлектрических сред нормальная составляющая вектора терпитразрыв, а нормальная составляющая вектора непрерывна. Граничные условия для касательных составляющих векторов D и E следуют из соотношения, описывающего циркуляцию вектора напряженности электрического поля. Построим вблизи границы раздела прямоугольный замкнутый контур длины l и высоты h (рис. 2.7).

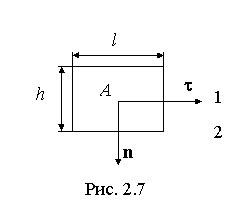Учитывая, что для электростатического поля

,

и обходя контур по часовой стрелке, представим циркуляцию вектора E в следующем виде:

,

где - среднее значениеE_n на боковых сторонах прямоугольника. Переходя к пределу при , получим для касательных составляющихE

.

Для касательных составляющих вектора электрической индукции граничное условие имеет вид:

Таким образом, при переходе через границу раздела диэлектрических сред касательная составляющая вектора непрерывна, а касательная составляющая вектора терпитразрыв. Преломление линий электрического поля. Из граничных условий для соответствующих составляющих векторов E и D следует, что при переходе через границу раздела двух диэлектрических сред линии этих векторов преломляются (рис. 2.8). Разложим векторы E₁ и E₂ у границы раздела на нормальные и тангенциальные составляющие и определим связь между углами ипри условии. Легко видеть, что как для напряженности поля, так и для индукции справедлив один и тот же закон преломления линий напряженности и линий смещения

.

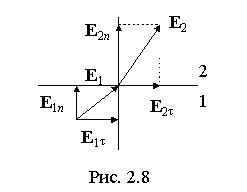
При переходе в среду с меньшим значением угол, образуемый линиями напряженности (смещения) с нормалью, уменьшается, следовательно, линии располагаются реже. При переходе в среду с большей линии векторовE и D, напротив, сгущаются и удаляются от нормали.

30.Электрическая ёмкость проводника, конденсатор

Электрическая ёмкость — характеристика проводника, мера его способности накапливать электрический заряд. В теории электрических цепей ёмкостью называют взаимную ёмкость между двумя проводниками; параметр ёмкостного элемента электрической схемы, представленного в виде двухполюсника. Такая ёмкость определяется как отношение величины электрического заряда к разности потенциалов между этими проводниками.В системе СИ ёмкость измеряется в фарадах.

Для одиночного проводника ёмкость равна отношению заряда проводника к его потенциалу в предположении, что все другие проводники бесконечно удалены и что потенциал бесконечно удалённой точки принят равным нулю. В математической форме данное определение имеет вид: гдеQ — заряд, U — потенциал проводника.

Ёмкость определяется геометрическими размерами и формой проводника и электрическими свойствами окружающей среды (её диэлектрической проницаемостью) и не зависит от материала проводника. К примеру, ёмкость проводящего шара радиуса R равна (в системе СИ):

Конденса́тор — двухполюсник с определённым значением ёмкости и малой омической проводимостью; устройство для накопления заряда и энергии электрического поля. Конденсатор является пассивным электронным компонентом. Обычно состоит из двух электродов в форме пластин (называемых обкладками), разделённых диэлектриком, толщина которого мала по сравнению с размерами обкладок.

Конденсатор в цепи постоянного тока может проводить ток в момент включения его в цепь (происходит заряд или перезаряд конденсатора), по окончании переходного процесса ток через конденсатор не течёт, так как его обкладки разделены диэлектриком. В цепи же переменного тока он проводит колебания переменного тока посредством циклической перезарядки конденсатора, замыкаясь так называемым током смещения.

При изменении частоты изменяются диэлектрическая проницаемость диэлектрика и степень влияния паразитных параметров — собственной индуктивности и сопротивления потерь. На высоких частотах любой конденсатор можно рассматривать как последовательный колебательный контур, образуемый ёмкостью С, собственной индуктивностью L_c и сопротивлением потерь R_n.

Резонансная частота конденсатора равна

При конденсатор в цепи переменного тока ведёт себя каккатушка индуктивности. Следовательно, конденсатор целесообразно использовать лишь на частотах , на которых его сопротивление носит ёмкостный характер. Обычно максимальная рабочая частота конденсатора примерно в 2—3 раза ниже резонансной.

Конденсатор может накапливать электрическую энергию. Энергия заряженного конденсатора: , где—напряжение (разность потенциалов), до которого заряжен конденсатор.