25.Теорема Гаусса, примеры ее применения

Теорема Гаусса— основная теоремаэлектродинамики, которая применяется для вычисления электрических полей, входит в системууравнений Максвелла. Она выражает связь между потоком напряжённости электрического поля сквозь замкнутую поверхность и зарядом в объёме, ограниченном этой поверхностью.

Применение теоремы Гаусса: Для вычисления электромагнитных полей используются следующие величины: объёмная плотность заряда; поверхностная плотность заряда:(где dS — бесконечно малый участок поверхности); линейная плотность заряда: (где dl — длина бесконечно малого отрезка.)

-Расчёт напряжённости бесконечной плоскости

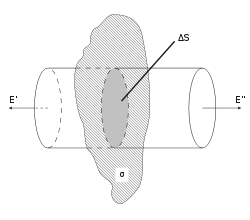Рассмотрим поле, создаваемое бесконечной однородной заряженной плоскостью. Пусть поверхностная плотность заряда плоскости одинакова и равна σ. Представим себе мысленно цилиндр с образующими, перпендикулярными к плоскости, и основанием ΔS, рас положенным относительно плоскости симметрично. В силу симметрии E' = E'' = E. Поток вектора напряжённости равен 2EΔS. Применив теорему Гаусса, получим: из которого

-Расчёт напряжённости бесконечной нити

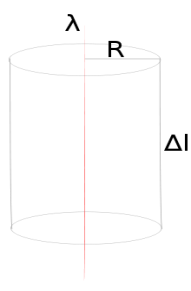Рассмотрим поле, создаваемое бесконечной нитью с линейной плотностью заряда, равной λ. Пусть требуется определить напряжённость, создаваемую этим полем на расстоянии R от нити. Возьмём в качестве гауссовой поверхности цилиндр с осью, совпадающей с нитью, радиусом R и высотой Δl. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:

В силу симметрии, модуль напряжённости в любой точке поверхности цилиндра будет одинаков. Тогда поток напряжённости через эту поверхность рассчитывается следующим образом:

Учитывается только площадь боковой поверхности цилиндра, так как поток через основания цилиндра равен нулю. Приравнивая 1 и 2 выражения, получим:

26.Потенциал электрического поля

Электростатический потенциа́л—скалярнаяэнергетическая характеристикаэлектростатического поля, характеризующая потенциальную энергию поля, которой обладает единичныйзаряд, помещённый в данную точку поля.

Электростатический потенциал равен отношению потенциальной энергиивзаимодействиязарядас полем к величине этого заряда:

Напряжённость электростатического поля E и потенциал связаны соотношением:Здесь—оператор набла, то есть в правой части равенства стоит вектор с компонентами, равнымичастным производнымот потенциала по соответствующим координатам, взятый с противоположным знаком

Воспользовавшись этим соотношением и теоремой Гауссадля напряжённости поля, легко увидеть, что электростатический потенциал удовлетворяетуравнению Пуассона. В единицах системыСИ:, где— электростатический потенциал (ввольтах),— объёмнаяплотность заряда(вкулонахна кубический метр), а—диэлектрическая проницаемостьвакуума (вфарадахна метр).

Поскольку потенциал может быть определён с точностью до произвольной постоянной, то непосредственный физический смысл имеет не сам потенциал, а разность потенциалов, которая определяется как: где:— потенциал в точке 1,— потенциал в точке 2,— работа поля по переносу пробного зарядаq^*из точки 1 в точку 2. При этом считается, что все остальные заряды при такой операции «заморожены».

В СИза единицу разности потенциалов принимаютвольт(В). Разность потенциалов между двумя точками поля равна одномувольту, если для перемещения между нимизарядав одинкулоннужно совершить работу в одинджоуль: 1В = 1 Дж/Кл (L²MT⁻³I⁻¹). ВСГСединица измерения потенциала не получила специального названия. Разность потенциалов между двумя точками равна одной единице потенциала СГСЭ, если для перемещения между ними заряда величиной однаединица заряда СГСЭнужно совершить работу в одинэрг. Приближенное соответствие между величинами: 1 В = 1/300 ед. потенциала СГСЭ