33. Частное и общее решение. Частный и общий интеграл. Задачи Коши.

1. Общее решение – функция, зависящая от независимой переменной и постоянной Y, удовлетворяющая 2ум условиям:

1. Для любого значения C=C₀, Y = U (x, C₀).

2. C=C₀, Y = U (x₁, C₀), что данная функция удовлетворяет начальному условию y(x₀) = y₀.

2. Всякое общее решение, найденное при значении С равное С₀, называется частным решением диф. Уравнения.

Y = u(x, C₀) - частное решение

3. Общим интегралом диф. Уравнения называется общее решение этого уравнения, записанное в неявном виде.

Ф (x, y, c) = 0 - общий интеграл

4. Частным интегралом диф. Уравнения называется частное решение диф. Уравнения, записанное в неявном виде.

Ф (х, у, с) = 0 – частный интеграл

Задача Коши:

Нахождение частного решения диф. Уравнения F (x, y, c) = 0 удовлетворяющего начальному условию.

y (x₀) = y₀

34. Дифференциальное уравнение с разделенными переменными и его решение.

Диф. Уравнение с разделенными переменными – уравнение вида:

f (x) dx + u (y) dy = 0

∫ f(x) dx + ∫ u (y) dy = C

F(x) + Ф(y) = C - общий интеграл

35. Дифференциальное уравнение с разделяющимися переменными и его решение.

Диф. Уравнение с разделяющимися переменными – это уравнение вида:

f₁(x) * u₁(y) dx + f₂(x) * u₂(y) dy = 0

Решение:

Разделим переменные.

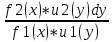+ = 0+= 0

36. Линейные однородные уравнения второго порядка с постоянными коэффициентами.

Линейные диф. Уравнения 2ого порядка с постоянными коэф. – это уравнение вида:

a₀*y” + a₁*y’ + a₂*y = f(x)

f(x) 0 – неоднородное

f(x) = 0 – однородное

a₀*k² + a₁*k + a₂ = 0 - характерное уравнение

Структура общего решения уравнения имеет вид:

y = C₁*y₁ + C₂*y₂

37. Элементы комбинаторики: размещения, перестановки, сочетания, свойство сочетаний.

Комбинаторика – это математическая наука, изучающая вопросы о том, сколько различных комбинаций, подчиненных тем или иным условием, можно составить.

1. Размещение.

Размещениями из N по M элементов называют такие соединения, в каждом из которых по M элементов и различаются такие соединения друг от друга только самими элементами и их порядками.

A_n^m = n (n-m+1) =

2. Перестановка.

Перестановками из N элементов называются такие соединения, в каждом из которых по N элементов U отличаются такие соединения только порядком самих элементов.

P_n = === n! P_n = n!

3. Сочетание.

Сочетаниями из N элементов по M называются такие соединения, в каждом из которых по M элементов и отличаются такие соединения только самими элементами.

= Свойство сочетания:=

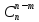
38. Виды событий. Примеры.

Виды событий:

1. Достоверное. Всегда произойдет при данном испытании.

Выстрел.

2. Невозможное. Никогда не произойдет при данном испытании.

Осечка.

3. Случайное. Может произойти, а может не произойти.

Попадание и промах.

4. Совместные. Если появление одного события не исключает появление другого события.

Попадание при 1 выстреле, не исключает промах при 2 выстреле.

5. Не совместные. Если появление одного из них исключает появление другого.

Попадание при 1 выстреле исключает промах при 1 выстреле.

6. Полная группа. Появится хотя бы одно из событий.

Кубик кидают, 1 из 6.

7. Противоположные. Если они не совместимы и образуют полную группу.

Попадание и промах.

8. Равновозможные. Имеют равные возможности их появления.

Как и в полной группе.

9. Благоприятствующие. Исходы, при которых случайное событие произойдет.