
08-Теория подобия
.pdf08-Теория подобия |
1 |
08-Теория подобия
1. Основные теоремы подобия.
Теорема 1. Подобные между собой процессы имеют один критерий подобия.
Теорема 2. Зависимость между переменными, характеризующими какойлибо процесс, может быть представлена в виде зависимости между критериями подобия.
Теорема 3. Подобные процессы, условия однозначности, которые подобны, и критерии, состоящие из величин, входящих в условия однозначности, численно одинаковы.
Критерии, составленные только из величин, входящих в условия однозначности, называются определяющими. Одинаковость (инвариантность) определяющих критериев является условием, которое должно быть выполнено для получения подобия.
Теория подобия позволяет, не интегрируя дифференциальные уравнения, получить из них критерии подобия и, используя экспериментальные данные, установить критериальные зависимости, которые будут справедливы для всех подобных между собой процессов. Но всегда надо помнить, что общего решения теория подобия не дает. Она позволяет только обобщить опытные данные в области, ограниченные условиями подобия.
Критерии подобия получают двумя методами:
a. если имеется математическая модель процесса, состоящая из системы дифференциальных и интегральных уравнений и условий однозначности, то критерии подобия получают различными преобразованиями этих уравнений.
Существует три метода таких преобразований:
o |
Метод подобных преобразований |
o |
Способ интегральных аналогов |
o Способ приведения уравнений к безразмерному виду |
|
b. |
Если нет математического описания, то критерии |
подобия для него могут быть получены с помощью анализа размерности величин, существенно влияющих на это явление.
Этот метод менее надежен, так как возможны ошибки и он существенно зависит от опыта и интуиции исследователя.
2. Приложения теории подобия к изучению процессов КТО. Условия теплового подобия систем с КТО.
Пусть имеются два подобных между собой процесса КТО.
|
|
|
|
|
|
|
|
|
08-Теория подобия |
2 |
||||||||||
|
|
|
|
|
|
|
|
|
1 Т1 |
1 |
Т1 |
|
(1) |
|
||||||
|
|
|
|
|
|
|
х |
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 Т2 |
2 |
Т2 |
(2) |
|
|
||||||
|
|
|
|
|
|
|
х2 |
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Так как эти системы подобны, то для них можно написать следующие |
||||||||||||||||||||
условия подобия и определить масштабы и константы подобия. |
|
|||||||||||||||||||
|
2 |
С |
сonst - масштаб коэффициента теплоотдачи. |
|
||||||||||||||||
1 |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
T2 |
|
|
|
СT |
сonst - масштаб подобия температур. |
|
|
||||||||||||
|
T1 |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
2 |
|
С |
сonst - масштаб подобия коэффициента теплопроводности. |
||||||||||||||||
|
1 |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
х2 |
|
y2 |
|
z2 |
С сonst - масштаб геометрического подобия системы. |
||||||||||||||
|
|
y1 |
|
|||||||||||||||||
|
х1 |
|
|
z1 |
|
|
|
|
|
|
|
|
|
|
|
|||||
На основании этих выражений, все переменные второй системы |
||||||||||||||||||||
представим через переменные первой системы: 2 |
1 С ; Т2 Т1 |
СТ ; |
||||||||||||||||||
2 1 С ; |
х2 х1 С |
|
|
|
|
|
|
|
|
|
|
|
||||||||
Полученные выражения подставим в выражение (2). |
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
С СТ 1 Т1 С |
СТ |
1 |
|
Т1 |
|
(3) |
|
||||
|
|
|
|
|
|
|
|
|
|
х |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
С |
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
||||
В уравнении (3) входят переменные только с индексом 1 и, следовательно, оно должно описывать первый процесс, для описания которого у нас есть выражение (1). Так как для первого процесса не может быть двух разных математических описаний, то уравнение (3) должно быть тождественно уравнению (1). Тождество уравнений (1) и (3) получится в том случае, если комплексы составленные из масштабов подобия (3) сократятся. А это возможно только при их взаимном равенстве, что и позволяет нам получить ограничительное условие по подобию этих систем КТО, вытекающие из дифференциального уравнения теплообмена.
С С 1 (4)
С
Подставим в (4) вместо масштабов подобия их значения через переменные и сгруппируем их всех по индексам .
2 2 1 1
2 1
Полученное условие (4) представляют в виде критерия подобия, согласно которому для всех подобных между собой процессов КТО оно постоянно.
Nu - критерий Нюссельта
Физический смысл критерия Нюссельта. Он характеризует связь между интенсивностью теплоотдачи и температурным полем в пограничном слое.

08-Теория подобия |
3 |
Его часто называют безразмерным коэффициентом теплоотдачи. Найдем критерии теплового подобия, вытекающие из общего дифференциального уравнения теплопроводности (уравнение Фурье-
Кирхгоффа).
Т |
|
T |
|
T |
T |
2 |
|
|
2T |
|
2T |
|
2T |
|
||||||
|
x |
|
y |
|
|
z |
|
a |
T a( |
|
|
|
|
|
) |
|||||
|
x |
|
|
|
x2 |
y2 |
z2 |
|||||||||||||
|
|
y |
z |
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
CT |
|
C CT |
|
CaCT |
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
C |
C |
|
|
C2 |
|
|
|
|
|
||||||
Из первого и третьего членов этого выражения получим:
CT |
|
CaCT |
|
CaC |
1 |
|
C |
C2 |
C2 |
||||
|
|
|
a idem Fo - критерий Фурье
2
Физический смысл критерия Фурье. Характеризует связь между скоростью изменения температурного поля, физическими свойствами и размерами тела.
Его часто называют безразмерным временем.
Из второго и третьего членов выражения получим:
CT С |
|
CaCT |
|
C C |
1 |
C |
C2 |
|
|||
|
|
Cа |
|||
idem Pe - критерий Пекле
а
Физический смысл критерия Пекле. Является мерой отношения молекулярного и конвективного переноса теплоты в потоке.
а - коэффициент температуропроводности;- конвективная составляющая;
Следовательно, при тепловом подобии двух или нескольких систем КТО для любых сходственных их точек, критерии подобия Фурье, Пекле и Нюссельта должны иметь одни и те же значения.
При экспериментальном изучении КТО уравнение подобия имеет вид:
|
|
|
|
|
Nu f Fo;Re;Pe;Gr |
|
|
Pe |
|
|
или |
Nu f Fo;Re;Pr;Gr , |
|
где Pr |
|
- критерий Прантля. |
||||
|
|
|||||
|
Re a |
|
||||
Re – критерий Рейнольдса; |
Gr – критерий Грасгофа; |
|||||
Критерии для полного подобия систем КТО требует выполнения равенства критериев Re и Gr, вытекающих из уравнения Навье-Стокса и обеспечивающих гидромеханическое подобие систем КТО.

08-Теория подобия |
4 |
3.Приложение теории подобия к изучению процессов движение газов
впечах. Условие гидромеханического подобия систем КТО.
Уравнение Навье-Стокса:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
2 |
2 |
2 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
gx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
x |
|
y |
|
z |
|
|
|
|
|
2 |
|
2 |
|
2 |
||||||||||||||||
|
|
|
z |
|
|
|
x |
y |
z |
|
||||||||||||||||||||||
|
|
|
|
|
|
x |
|
|
y |
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
C C |
|
C C2 |
|
|
|
C |
P |
|
|
C C |
|
|
(*) |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
C Cg |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
C |
|
|
|
C |
C2 |
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
C |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Приравняв первый и второй члены выражения (*), получим:
C C C C2 C C 1
C C C
idem Ho- критерий Гомохронности
Физический смысл критерия Гомохромности. Характеризует скорость изменения поля скоростей течения среды во времени.
Приравняв второй и третий члены выражения (*), получим:
C C2 |
C2 |
1 |
|
|
C Cg |
|
|
|
СgC |
||
C |
|
||
2 idem Fr - критерий Фруда
g
Физический смысл критерия Фруда. Является мерой отношения сил инерции и сил тяжести в однородном потоке.
Приравняв второй и четвертый члены выражения (*), получим:
C C2 |
C |
|
|
C |
P |
|
1 |
||
|
|
|
|
P |
|
|
|
||
C |
|
C |
|
C С2 |
|||||
|
|
|
|||||||
|
|
|
|
|
|
||||
P |
idem Eu - критерий Эйлера |
|
2 |
||
|
Физический смысл критерия Эйлера. Является мерой отношения сил давления и сил инерции в потоке.
Приравняв второй и пятый члены выражения (*), получим:
C C2 |
C C |
|
C C |
С |
1 |
|
|
|
|
|
|
|
|
C |
C2 |
|
C |
|
|
|
idem Re - критерий Рейнольда
Физический смысл критерия Рейнольда. Характеризует гидродинамический режим потока и является мерой отношения в потоке сил инерции и молекулярного трения.
- кинематический коэффициент вязкости. Следовательно Re
|
|

08-Теория подобия |
5 |
При изучении движения газов и жидкостей в рабочем пространстве печи и печных системах, критериальное уравнение представляют в виде функции:
f Ho;Fr;Eu;Re 0
Вид этой функции для конкретной системы определяют экспериментально и обычно представляют в виде:
f Ho;Fr;Re Eu
Следовательно, для гидродинамического подобия двух или нескольких потоков газа или жидкости для любых сходственных их точек, критерии Но, Fr и Re должны иметь одинаковые числовые значения. При этом обязательным условием является соблюдение геометрического подобия системы.
При изучении движения газов или жидкостей в некоторых случаях используют видоизмененные критерии гидродинамического подобия. Например, при исследовании движения печных газов, вызываемого разностью удельных весов или плотностей, точное измерение скоростей затруднительно, и поэтому скорость исключают из рассмотрения, применяя вместо критерия Фруда критерий Галилея (Ga), который представляет собой:
Ga |
Re2 |
2 2 |
|
g |
|
g 3 |
|
|
|
|
|
|
|
|
|
|
2 |
2 |
2 |
||||
|
Fr |
|
|
||||
Физический смысл критерия Галилея. Является мерой отношения сил молекулярного трения и сил тяжести в потоке.
Если умножить критерий Галилея на отношения плотностей газа в двух точках системы, то получим критерий Архимеда (Ar), который учитывает подъемную силу газа.
|
|
0 |
|
g 3 |
|
0 |
|
||
Ar Ga |
|
|
|
|
|
|
|
||
|
|
|
2 |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Если разность плотностей газа определяется разностью температуры, то:
0 Т
где - коэффициент объемного расширения газа. Подставив последнее уравнения в выражения критерия Архимеда, получим критерий Грасгофа.
g 3
Gr Ga Т T
2
Физический смысл критерий Грасгофа. Характеризует взаимодействия сил молекулярного трения и подъемные силы, обусловленные различием плотностей в отдельных точках неизотермического потока.
При изучении движения газов или жидкостей искомой величиной чаще всего является перепад давлений, то есть потеря напора от различных сопротивлений на пути движения газов или жидкостей. Поэтому одним из
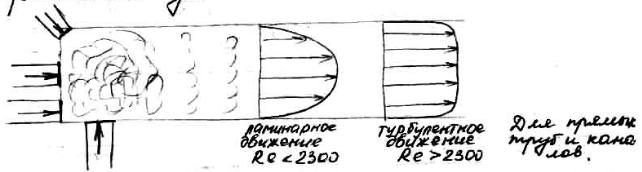
08-Теория подобия |
6 |
основных критериальных уравнений, описывающих закономерности вынужденного движения газов или жидкостей является уравнение Эйлера.
Eu f (Re)
Лекция 12
4. Приближенное моделирование.
Опыт показал, что точное соблюдение всех условий подобия, вытекающих из теории подобия затруднительно, а очень часто и невозможно. Поэтому в научной и в инженерной практики очень широкое применение нашло приближенное моделирование, которое как показали многочисленные исследования, дает вполне приемлемую для техники точность. Приближенное моделирование процессов теплообмена и движения газов и жидкостей оказалось возможным в следствии особенностей движения вязких газов и жидкостей, заключающихся в стабильности и в автомодельности потоков, а также в возможности применения локального теплового моделирования.
Стабильность – это свойство газов или жидкостей принимать вполне определенное распределение скоростей при движении по каналам различной формы, независящее от условий входа газа или жидкости в этот канал и определяемая только характером движения, то есть величиной критерия Рейнольда. Как бы не искажалась на входе канала картина распределения скоростей, при дальнейшем движении по каналу все искажения сглаживаются и поток принимает эпюру скоростей строго соответствующую ламинарному или турбулентному режиму движения.
Автомодельность (самоподобие) газовых или жидкостных движениях заключается в том, что в широких пределах областей ламинарного и турбулентного режимов движения эпюра скоростей не зависит от численного значения критерия Рейнольда, а следовательно от скорости и расхода газа и жидкости, если при этом не происходит изменения характера движения.
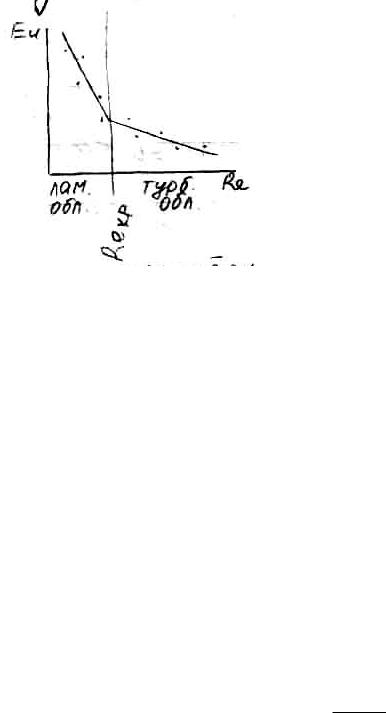
08-Теория подобия |
7 |
Сущность локального теплового моделирования заключается в том, что подобие теплообмена устанавливается не по всей печи или агрегату в целом, что часто очень затруднительно, а по отдельным их участкам на которых поочередно и исследуется теплообмен. Результаты такого моделирования соответствующим образом суммируют и получают общую картину теплообмена по всей печи в целом.
При моделировании КТО определяют значение к в печах и воздухоподогревателях (в регуляторах и в регенераторах), а также оценивают роль отдельных участков и поверхностей тепловой работы печей.
5.Порядок расчета КТО по уравнениям подобия.
Теплоотдачу при естественном движении газа или жидкости в свободном пространстве можно рассчитать по формуле Михеива М.А.
Nu C Gr Pr nm (*)
Индекс m означает, что при расчетах теплоотдачи за определяющую температуру по которой находят значения физических параметров, входящих в критерии, принимают:
tопр tпов tср
2
C и n – коэффициенты, которые находятся из таблицы.
Gr Pr mn |
10 3...5 102 |
C 1.18 |
n 0.125 |
(**) |
(Gr Pr)mn |
5 102...2 107 |
C 0.54 |
n 0.25 |
|
(Gr Pr)mn |
2 107...1013 |
C 0.135 |
n 0.33 |
|
При расчетах критериев за определяющий размер принимают:
1. |
При движении газов и жидкостей внутри труб и |
|||
каналов гидравлический (эквивалентный) диаметр dэкв |
|
4F |
, где F – площадь |
|
|
||||
|
|
|
S |
|
поперечного сечения канала заполненного газом или жидкостью; S – периметр канала, соприкасающегося с газом или жидкостью.
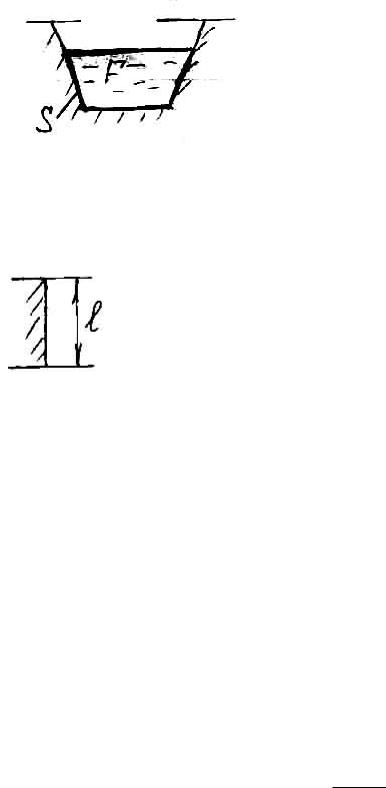
08-Теория подобия |
8 |
|
|
|
|
|
|
|
|
|
|
|
4 R2 |
|
S S |
1 |
S |
2 |
S |
3 |
d |
гидр |
d |
экв |
|
|
2R |
|
||||||||||||
|
|
|
|
|
|
2 R |
||||||
2.При наружном обтекании труб dнаружное
3.При обтекании вертикальных плит равна длине плиты по направлению движения среды.
4.При горизонтальных плитах равна меньшей стороне плиты Формула (*) применима для любых вязких газов и жидкостей, у которых
Pr больше либо равен 0.7, и для тел любой формы и любого размера. По ней рассчитывают теплообмен конвекцией наружных поверхностей печей с окружающим воздухом.
Порядок расчета.
1.Развертывают значения критериев, входящих в формулы:
|
|
|
|
Cr |
|
g 3 |
T |
|
|
|||
|
Nu |
|
k |
|
|
|
Pr |
|
|
|
||
|
|
|
2 |
|
a |
|||||||
|
|
|
|
|
|
|
|
|||||
где |
- коэффициент теплоотдачи; |
- коэффициент объемного |
||||||||||
расширения; - коэффициент кинематической вязкости; а- коэффициент температуропроводности.
2. Вычисляют определяющую температуру как среднеарифметическую:
tопр tпов tср
2
3.По определяющей температуре и справочным данным для физических свойств критериев определяют значение параметров, входящих в критерии: , ,а, ,Pr
4.Рассчитывают численное значение Cr Pr
5.По величине Cr Pr из таблицы (**) находят значения С и n.
6.По формуле (*) находим численное значение критерия Nu.
7.По значению Nu находят к .
08-Теория подобия |
9 |
8. По формуле закона Ньютона находят количество теплоты, передаваемое конвекцией: Qкон к Тср Тповм Fм
Теплоотдачу при вынужденном движении газа или жидкости, при турбулентном характере движения рассчитывают по формуле Михеева:
|
|
|
|
|
Prf |
0.25 |
|
|
Nu |
|
0.021Re0.8 |
Pr0.43 |
|
|
|
|
|
|
Pr |
|
||||||
|
f |
f |
f |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Индекс f означает, что за определяющую температуру принимается |
||||||||
средняя температура газа или жидкости. |
|
|
|
|
|
|
||
Pr вычисляют по температуре поверхности тела, |
а определяют по |
|||||||
вспомогательной таблице. |
|
|
|
|
|
|
|
|

|
|
|
|
08-Теория подобия |
|
10 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Re |
|
|
|
|
при |
L |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
5 |
10 |
|
15 |
|
20 |
30 |
40 |
50 |
|
104 |
1.65 |
1.50 |
1.34 |
1.23 |
|
1.17 |
|
1.13 |
1.07 |
1.03 |
1.0 |
|
2 104 |
|
|
|
|
|
|
|
|
|
|
|
|
5 104 |
|
|
|
|
|
|
|
|
|
|
|
|
105 |
|
|
|
|
|
|
|
|
|
|
|
|
106 |
1.14 |
1.11 |
1.08 |
1.05 |
|
1.04 |
|
1.03 |
1.02 |
1.01 |
1.0 |
|
L – длинна канала; - гидравлический диаметр;
Из таблицы видно, что при высокой турбулентности стабилизация приходит более быстро.
Эту формулу можно применять к трубам и каналам любой формы поперечного сечения, для всех газов или жидкостей при Ref=104…5 106 и при
Prf=0.6…2500
