Определение 1

Пусть M

0

(x0

, x0,..., x

0 ) Rn и δ > 0 - вещественное число. δ -

окрестностью

1

2

n

точки

M

0

называется

множество точек M (x , x

2

,..., x

n

) Rn ,

для которых

1

справедливо: ρ(M 0, M ) < δ. δ -окрестность точки M 0 обозначается Uδ(M 0 ).

Пример 1

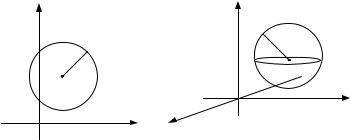
Если

M 0 R2 ,

то Uδ(M 0 )- открытый круг (граница не входит в это множество) с

центром в точке M 0

и радиусом δ (рис.1). Если M 0 R3, то Uδ(M 0 )- открытый шар

Определение 2

Пусть M

0

(x0

, x0,..., x0 ) Rn и δ > 0 . Проколотой δ - окрестностью

точки M

0

1

2

n

Uδ(M 0 ) \ {M 0},

называется

множество

то

есть

множество

точек

M (x , x

2

,..., x

n

) Rn ,

для которых справедливо: 0 < ρ(M

0

, M ) < δ. Проколотая δ -

1

окрестность точки M 0 обозначается U&δ(M 0 ).

Определение 3

Точка

M 0

D R n называется

внутренней

точкой

множества

D ,

если

Uδ(M 0 ) D .

Определение 4

Точка

M 0

называется

граничной

точкой

множества

D Rn , если

ее

любая

окрестность содержит как точки множества D , так и точки, не принадлежащие D .

Определение 5

Точка

M 0

называется

предельной

точкой

множества

D Rn , если

любая ее