
- •6. Дифференциальное исчисление функций нескольких переменных (14 часов)
- •1. Функции нескольких переменных
- •Определение 1
- •Пример 1
- •Пример 2
- •Пример 3
- •Определение 2
- •Определение 3
- •Теорема
- •Определение 1
- •Пример 1
- •Определение 2
- •Определение 3
- •Определение 4
- •Определение 5
- •Определение 6
- •Пример 2
- •Пример 3
- •Определение 7
- •Определение 8
- •Пример 4
- •Определение 1
- •Пример 1
- •Решение
- •Определение 2
- •Пример 2
- •Пример 3
- •Пример 4
- •Определение 3
- •Определение 4
- •Теорема 1
- •Доказательство
- •Определение 5
- •Определение 6
- •Пример 5
- •Теорема 2
- •Теорема 3
- •Определение 1
- •Определение 2
- •Пример 1
- •Решение
- •Пример 2
- •Решение
- •Пример 3
- •Решение
- •Теорема 1
- •Доказательство
- •Теорема 2
- •Пример 4
- •Решение
- •2.2. Дифференцируемая функция. Условия дифференцируемости
- •Определение 1
- •Теорема 1. (Необходимое условие дифференцируемости)
- •Доказательство
- •Следствие 1
- •Следствие 2
- •Пример
- •Теорема 2. (Достаточное условие дифференцируемости).
- •Доказательство
- •2.3. Производная сложной функции. Полная производная
- •Теорема 1
- •Доказательство
- •Пример 1
- •Решение
- •Следствие 1
- •Пример 2
- •Решение
- •Пример 3
- •Решение
- •3. Дифференциал функции нескольких переменных
- •3.1. Определение дифференциала функции нескольких переменных и его свойства. Инвариантность формулы дифференциала
- •Определение
- •Пример 1
- •Решение
- •Теорема 1
- •Пример 2
- •Решение
- •3.2. Геометрический смысл дифференциала функции двух переменных. Уравнение касательной плоскости и нормали к поверхности.
- •Теорема
- •Доказательство
- •Следствие 1
- •Следствие 2
- •Пример
- •Решение
- •3.3. Приближенные вычисления и оценка погрешностей
- •Пример
- •Решение
- •4. Частные производные и дифференциалы высших порядков функции нескольких переменных
- •Определение 1
- •Теорема 1
- •Пример 1
- •Решение
- •Определение 2
- •Теорема 2
- •Доказательство
- •Пример 2
- •Решение
- •Пример 3
- •Решение
- •5. Производные функций нескольких переменных, заданных неявно
- •Определение
- •Теорема 1
- •Доказательство
- •Пример 1
- •Решение
- •Пример 2
- •Решение
- •Пример 1
- •Решение
- •Определение
- •Теорема
- •Пример 2
- •Решение
- •6. Экстремум функции нескольких переменных
- •6.2. Экстремум функции двух переменных
- •Определение 1
- •Определение 2
- •Теорема 1
- •Доказательство
- •Следствие
- •Определение
- •Теорема2
- •Доказательство
- •Пример 1
- •Теорема 3
- •Доказательство
- •Пример 2
- •Решение
- •Пример
- •Решение
- •6.4. Наименьшее и наибольшее значения функции нескольких переменных
- •Теорема
- •Пример
- •Решение
- •6. Дифференциальное исчисление функций нескольких переменных (10 часов)
5.Производные функций нескольких переменных, заданных неявно
5.1.Неявная функция. Дифференцируемость неявной функции. Формула
для частных производных функции двух переменных, заданной неявно.
Определение
Функция w = f (x1, x2 ,..., xn ) называется заданной неявно в окрестности точки (x10 , x20 ,..., xn0 , w0 ), если задано уравнение F(x1, x2 ,..., xn , w)= 0 и если:
• |
F (x10 , x20 ,..., xn0 , w0 )= 0 ; |
|
|
|
• |
M (x1, x2 ,..., xn ) Uδ(M 0 ) |
|
единственное |
w Uδ(w0 ): |
|
F(x1, x2 ,..., xn , w)= 0 . |
|
|
(x0 , y0 , z0 ), для |
В частности, уравнение F(x, y, z)= 0 |
в окрестностях тех точек |
|||
которых уравнение F(x0 , y0 , z)= 0 имеет хотя бы один корень функцию z = f (x, y), значения которой равны корням этого уравнения.
При этом уравнение F(x, y, z)= 0 иногда может быть разрешено относительно z , а
иногда нет. Не следует путать вопрос о существовании неявной функции с вопросом получения ее в виде явной зависимости. Следующая теорема дает условия существования, единственности и дифференцируемости неявной функции.
Теорема 1
Если функция F(x1, x2 ,..., xn , w):
•непрерывна в окрестности точки (x10 , x20 ,..., xn0 , w0 );
•имеет в этой окрестности непрерывные частные производные по всем переменным;
•F (x10 , x20 ,..., xn0 , w0 )= 0 ;
•Fw′ (x10 , x20 ,..., xn0 , w0 )≠ 0 ;
то уравнение F(x1, x2 ,..., xn , w)= 0 задает в окрестности точки (x10 , x20 ,..., xn0 , w0 ) однозначную дифференцируемую функцию w = f (x1, x2 ,..., xn ), для которой справедливо
w0 = F(x10 , x20 ,..., xn0 ).
Доказательство
В силу сложности и громоздкости доказательства этой теоремы, рассмотрим ее доказательство только для функции двух переменных y = f (x), заданной неявной зависимостью F(x, y)= 0 , где функция F(x, y) непрерывна и дифференцируема в
некоторой δ |
- окрестности точки (x0 , y0 ) и |
Fy′ (x0 , y0 )≠ 0 . |
Если точка |
|||||
(x0 + |
x, y0 + |
y) принадлежит этой окрестности, то |
|
|
|
|
||
|
|
F(x0 , y0 )= 0 и F(x0 + x, y0 + y)= 0 , |
|
|||||
тогда и |
F (x0 + |
x, y0 + y)− F (x0 , y0 )= 0 . Для левой части последнего равенства |
||||||
можно использовать теорему Лагранжа. |
|
|
|
|
||||
F (x0 + x, y0 + y)− F (x0 , y0 )= [F (x0 + x, y0 + y)− F (x0 + x, y0 )]+ |
||||||||
+[F(x0 + x, y0 )− F(x0 , y0 )]= |
∂F |
(x0 + x, y0 ) |
y + |
∂F |
(x0 , y0 ) |
x = 0 . |
||
|
|
|||||||
|
|
|
∂y |
|
∂x |
|
||
29
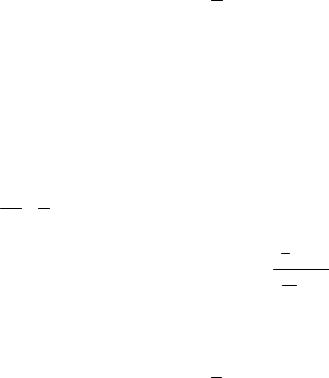
|
|
|
|
|
|
|
y = − |
|
∂F |
(x |
+ |
|
x, y ) |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Из последнего равенства следует, что |
|
|
|
|
∂x |
0 |
|
|
|
|
|
0 |
. Переходя в нем к пределу |
|||||||||||||||||||
|
|
|
|
|
|
∂F (x , y |
|
|
) |
|||||||||||||||||||||||
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂y |
0 |
|
|
|
|
|
|
|
|
|
|
|
|||||
при x → 0 и учитывая, что частные производные непрерывны, получим |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
∂F (x , y |
0 |
) |
|
|
|
|
|
|
|
∂F (x |
, y |
0 |
) |
|
|
||||||||||||
|
|
|
|
|
∂x |
0 |
|
|
|
|
|
|
|
|
∂x |
0 |
|
|
|
|
|
|||||||||||
f ′(x0 )= lim − |
|
|
|
|
|
|
|
|
|
|
|
|
= − |
|
|
|
|
|
. |
|
||||||||||||
|
∂F |
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
||||||||||||||||
x→0 |
|
|
|
|
|
|
(x0 + x, y0 ) |
|
|
|
|
|
|
(x0 , y0 ) |
|
|
||||||||||||||||
|
|
∂y |
|
|
|
|
|
|
∂y |
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
ЗАМЕЧАНИЕ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Мы не только доказали дифференцируемость |
функции |
|
y = f (x), но и |
получили |
||||||||||||||||||||||||||||
формулу для вычисления ее производной. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
y′x = − |
∂x |
. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Аналогично доказывается, что функция |
|
|
двух |
|
переменных z = f (x, y), |
заданная |
||||||||||||||||||||||||||
уравнением F(x, y, z)= 0 , где F(x, y, z) - |
дифференцируемая по всем переменным |
|||||||||||||||||||||||||||||||
функция, дифференцируема в точках, |
в которых |
|
∂F |
|
≠ 0 |
и ее частные производные |
||||||||||||||||||||||||||
|
|
∂z |
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
вычисляются по формулам |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
∂z = − |
|
∂F |
|
|
∂z |
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
∂x |
; |
|
|
= − |
|
∂y |
. |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
∂x |
∂F |
|
|
|
∂y |
|
|
|
|
|
|
|
|
∂F |
|
|
|
|
|
|
|
|
|
|
|
|||||||
∂z |
|
|
|
|
|
|
|
|
|
|
∂z |
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Пример 1
Выясните, в каких точках дифференцируема функция y = f (x), заданная неявно, и
вычислите ее производную, если xy + exy = 0 .
Решение |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
F(x, y)= |
x |
+ exy . Поэтому |
функция дифференцируема |
во всех |
точках, |
за |
||||||||||||
y |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
исключением |
тех, |
где |
∂F |
|
= 0 . Поскольку |
∂F |
= − |
|
x |
+ exy x , |
то |
функция |
||||||
|
|
|
|
∂y |
|
∂y |
|
y2 |
|
|
|
|
||||||
дифференцируема |
везде, |
где |
выполняется условие |
− |
|
x |
+ exy x ≠ 0 . |
Так |
как |
|||||||||
|
y2 |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
∂∂Fx = 1y + exy y , то
1 +exy y
y′x = − −yx +exy x . y2
Пример 2
Выясните, в каких точках дифференцируема функция z = f (x, y), заданная неявно, и
вычислите ее производную, если xz + z cos(xy)= 0 .
30
