
15. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ
.docx
4.5. ОСНОВЫ ГЕОМЕТРИЧЕСКОЙ ТЕОРИИ ДИФРАКЦИИ
Лучевые решения, основанные на законах лучевой акустики (ЛA) (см. 2.4), можно использовать при исследовании более сложных задач о рассеянии высокочастотного поля методом геометрической теории дифракции (ГТД). Отличие законов ГТД от законов ЛА состоит в том, что в ГТД наряду с отражением и преломлением постулируются и другие способы образования лучей. Во всех случаях, когда при падении волны на тело (или границу раздела) возникает граница тень—свет для геометрических волн (лучей), т. е. геометроакустическое решение претерпевает разрыв, постулируется образование дополнительных дифракционных полей, компенсирующих этот разрыв. Лучи дифракционных полей порождаются лучами первичного поля, касающимися тела или падающими на изломы его поверхности (рёбра, острия). Иными словами, в ГТД по сравнению с ЛА расширяется вторая группа законов: первая группа сохраняется в ГТД без изменений. Дополнительные специфические для ГТД законы во многом сходны с законами ЛА второй группы. Всего имеется четыре дополнительных закона: два из них определяют направления дифракционных лучей, два других — их амплитуды. Запишем сначала два первых закона.

Рис. 4.34. Разновидности дифракционных полей
в рамках геометрической теории дифракции
1. Множество (конгруэнция) дифракционных лучей порождается не всеми падающими лучами, а только некоторыми:
а) лучами, падающими на неоднородные участки тела S — острия, рёбра, линии разрывов кривизны (рис. 4.34, а, б);
б) лучами, касающимися тела (рис. 4.34, в). Иными словами, дифракционные лучи порождаются только теми падающими лучами, которые образуют границу свет—тень («крайние лучи» с точки зрения ЛА).
Каждый луч первичного поля, относящийся к указанной выше категории лучей, порождает бесконечное множество дифракционных лучей. При падении луча первичного поля на острие (см. рис. 4.34, а) дифракционные лучи уходят от него во всех направлениях, тем самым образуя сферическую волну. При падении луча на ребро (см. рис. 4.34, б) дифракционные лучи в каждой его точке образуют конус. Угол с раствора конуса равен углу между касательной к ребру и падающим лучом, следовательно,
cos ω = cos Ω . (4.91)
Закон (4.91) можно рассматривать как обобщение закона зеркального отражения, определяющего направление отражённого луча.
Закон образования дифракционных лучей в области тени гладкого выпуклого тела отличен от закона образования лучей у остриев и рёбер. В этом случае дифракционные лучи срываются с поверхности теневой части тела. Дифракционные волны такого типа получили название волн соскальзывания. Поясним схему образования лучей в данном случае.
2. Каждый луч падающей волны, касающийся тела, порождает на поверхности тела «поверхностный» луч Тb (рис. 4.34, в), который является геодезической (кратчайшей) линией на поверхности тела. Его направление в точке Т горизонта аа', т. е. в месте образования, совпадает с направлением падающего луча. Множество (конгруэнция) лучей волны соскользывания отрывается по касательной от семейства поверхностных лучей.
Два закона ГТД, определяющие амплитуды дифракционных полей, формулируются следующим образом.
3. Амплитуда дифракционного луча пропорциональна амплитуде порождающего первичного луча в точке падения.
С учётом того, что дифракционные поля подчиняются первой группе законов ЛА, они могут быть записаны в форме
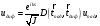
где s — эйконал;
J — якобиан перехода к лучевым координатам — величина, пропорциональная площади поперечного сечения лучевой трубки (см. 2.4);
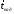 ,
, —
орты падающего и дифракционного
лучей;
—
орты падающего и дифракционного
лучей;
uпад — амплитуда падающей волны в той точке ребра или острия, из которой выходит рассматриваемый дифракционный луч, или для случая дифракции на гладком теле — в той точке горизонта, в которой возникает поверхностный луч, порождающий рассматриваемый дифракционный луч.
Величина D называется
коэффициентом дифракции. Она
вычисляется в соответствии с четвёртым
законом ГТД.
называется
коэффициентом дифракции. Она
вычисляется в соответствии с четвёртым
законом ГТД.
4. Коэффициент (матрица) дифракции D определяется локальными особенностями геометрии тела в окрестности падающего луча (в случае остриёв или рёбер) или в окрестности поверхностного луча между точкой падения и точкой отрыва дифракционного луча (в случае гладкого тела).
Каков физический
смысл коэффициента дифракции? Из законов
ЛА следует, что поле вдоль каждого
дифракционного луча можно трактовать
как поле, как бы излучаемое источником,
расположенным в точке выхода луча из
ребра или острия. Различным лучам
соответствуют источники с различной
амплитудой. С этой точки зрения D —
это амплитуда источника, соответствующего
лучу, уходящему в направлении
—
это амплитуда источника, соответствующего
лучу, уходящему в направлении
 при падении плоской волны единичной
амплитуды в направлении
при падении плоской волны единичной
амплитуды в направлении
 .
.
Понятие коэффициента дифракции при более строгом подходе нуждается в уточнении. Пусть, например, амплитуда первичного поля обращается в нуль на луче, порождающем рассматриваемые дифракционные лучи. Означает ли это, что амплитуда дифракционнoro поля также обращается в нуль? Очевидно, она будет хотя и мала, но не равна нулю, а формула (4.92) будет заведомо неприменима. В этом случае дифракционное поле (в главном члене его асимптотического представления) пропорционально значению первой производной амплитуды первичного поля вдоль фронта.
Каким образом связаны перечисленные выше законы дифракционных лучей с законами ЛА?
Первые два закона ГТД и ЛА можно рассматривать как следствие обобщённого принципа Ферма, согласно которому путь вдоль акустического луча от источника до точки наблюдения является экстремальным. Обобщение обычного принципа Ферма заключатся в том, что рассматриваются экстремальные пути при дополнительных условиях. Так, закон зеркального отражения есть следствие принципа Ферма при следующем дополнительном условии: луч должен соприкоснуться с поверхностью тела. Закон (4.91) образования конуса дифракционных лучей у ребра следует из принципа Ферма при введении такого дополнительного условия: путь должен содержать какую-либо точку ребра.
Вторые два закона ГТД сохраняют основное свойство ЛА — локальность полей. Амплитуда дифракционного поля в заданной очке зависит только от ширины лучевой трубки и от того, каковы первичное поле и форма тела в окрестности точки дифракционного луча, проходящего через рассматриваемую точку.
На основе постулированных Келлером законов ГТД разработан излагаемый ниже алгоритм решения задачи дифракции, состоящий из трёх правил:
1. Решение отыскивается в виде суммы полей лучевого типа:
и =
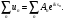 (4.93)
(4.93)
Одно из слагаемых — первичное поле. Каждое из полей отлично от нуля в области, границами которой являются поверхность тела и границы свет—тень этого поля.
2. Все слагаемые в сумме (4.93), за исключением первичного поля (оно считается заданным), определяется из первичного поля или по законам ЛА, или по законам ГТД.
Следует иметь в виду, что отражённые, преломлённые и дифракционные поля могут образовываться из первичного не только непосредственно, но и в результате сложной последовательности отражений, преломлений и дифракций. Волны, образующиеся непосредственно из первичной волны, называются волнами первичного отражения, первичного преломления, первичной дифракции. Волны, образующиеся при отражении однократно отражённой волны,— двукратно отражёнными, при дифракции волны первичной дифракции — волнами вторичной дифракции и т. д. Волны, образующиеся путём сложной цепи последовательных дифракций, преломлений и отражений, специальных наименований не имеют.
При расчёте дифракционных полей с помощью ГТД важным является вопрос о выборе коэффициентов дифракции. Из сформулированного выше четвёртого закона ГТД следует, что коэффициенты дифракции одинаковы для тел, имеющих одинаковые локальные особенности геометрии тела и геометрии фронта падающей волны. Отсюда вытекает третье правило алгоритма решения задачи дифракции.
3. Коэффициент дифракции для рассматриваемой задачи находится из анализа точного решения сходной по геометрии простейшей (модельной) задачи.
Например, для
дифракции поля Ф
=
 [см. (2.66)] на
криволинейном отверстии в неплоском
экране модельной задачей является
задача дифракции плоской волны на
полуплоскости, касающейся поверхности
экрана и края отверстия в той точке
края, которая нас интересует.
[см. (2.66)] на
криволинейном отверстии в неплоском
экране модельной задачей является
задача дифракции плоской волны на
полуплоскости, касающейся поверхности
экрана и края отверстия в той точке
края, которая нас интересует.
Поскольку коэффициенты дифракции D определяют из модельных задач, применение ГТД ограничено имеющимся набором их решений. В настоящее время решены модельные задачи для многих двумерных случаев: дифракции на клине, гладком цилиндре и т. п. Гораздо хуже обстоит дело с решением модельных трёхмерных задач; здесь часто приходится ограничиваться приближёнными их решениями.
