17.4 Атом щелочного металла

Пусть атом щелочного металла имеет электронов. Тогда можно считать, чтоэлектронов вместе с ядром образуют остов, в электрическом поле которого движется внешний (валентный) электрон, довольно слабо связанный с остовом атома.

В некотором смысле атомы щелочных металлов являются водородоподобными, однако не полностью. Дело в том, что внешний электрон деформирует электронный остов и тем самым искажает поле, в котором движется. В первом приближении поле остова можно рассматривать как суперпозицию поля точечного заряда и поле точечного диполя, расположенного в центре остова. При этом ось диполя направлена все время к внешнему электрону.

Это позволяет представить потенциальную энергию внешнего электрона в поле такого остова как

, (17.28)

где – некоторая постоянная.

Решение уравнения Шредингера для электрона с потенциальной энергией (17.28) приводит к тому, что теперь дозволенные значения энергии в области(для связанных состояний внешнего электрона) будут зависеть от главного квантового числаи от орбитального квантового числа:

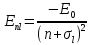, (17.29)

где =13,6 эВ,– поправка Ридберга (или квантовый дефект), зависящая от. Значения поправок определяются экспериментально. Например, для натрия эти значения равны

(17.30)

Таким образом, в атоме щелочного металла снимается вырождение по числу .

Схема энергетических уровней для лития представлена на рис. 5.

Рис. 5

Заметим, что у лития основным состоянием является , поскольку состояние суже занято двумя электронами, входящими в состав остова. Зависимость энергии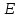электрона не только 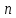от, но и отобъясняется тем, что в атоме щелочного металла внешний электрон находится в электрическом поле атомного остова, которое не кулоновское (не). Заряд остова не точечный, и распределение его несколько отличается от сферически-симметричного.

Правило отбора Излучение (и поглощение) происходит в результате перехода внешнего электрона с одного уровня на другой. Однако не все переходы возможны. Возможны лишь те, при которых орбитальное квантовое число внешнего электрона меняется на единицу:

(17.31)

Это означает, что разрешенными являются переходы лишь между - и- состояниями, между- и- состояниями и т.д. Заметим, что главное квантовое числоможет изменяться на любое целое число.

17.5 Принцип Паули. Заполнение электронных оболочек

Электроны в атомах могут находиться в различных состояниях, которым соответствуют разные наборы четверки квантовых чисел . Энергия электронов в атоме зависит оти. Однако в магнитном поле снимается вырождение по магнитному квантовому числу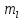и каждый-ый уровень расщепляется намелких подуровней (эффект Зеемана), и энергия электронов в атоме уже будет зависеть от трех квантовых чисел.

Распределение электронов по энергетическим уровням осуществляется согласно принципу Паули (1940г.):

в атоме не может быть электронов с одинаковыми значениями всех четырех квантовых чисел

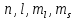
или

в каждом квантовом состоянии, характеризуемом набором квантовых чисел , определяющих некоторый уровень энергии, может находиться не более двух электронов с противоположно направленными спинами.

Кроме того, следует учитывать, что система частиц стабильна, когда ее потенциальная энергия минимальна.

Именно принцип Паули объяснил, почему электроны в атомах оказываются не все на самом нижнем энергетическом уровне.

Совокупность электронов атома с одинаковыми значениями квантового числа образуют так называемую оболочку. В соответствии со значениемоболочки обозначают большими буквами латинского алфавита следующим образом:

Значение	1	2	3	4	5	6
Оболочка

Оболочки подразделяют на подоболочки, отличающиеся квантовым числом 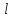. Различные состояния в подоболочке отличаются значениями квантовых чисели. Число состояний в подоболочке равно. Подоболочки обозначают в виде:

где цифра означает квантовое число .

Возможные состояния электронов в атоме и их распределение по оболочкам и подоблочками показано в таблице 1.

Ранее было показано, что данному значению соответствуетсостояний, отличающихся друг от друга значениями квантовых чисел(см. вывод формулы 17.8). Из таблицы 1 видно, что число возможных состояний воболочках равно соответственно 2, 8, 18. …, т.е. равно.

Оболочка
Подоболочка
	0	0	+1	0	-1	0		+1		0	-1	+2		+1	0	-1	-2
Число электронов в подоболочке	2	2	6				2		6				10
Число электронов в оболочке	2	8					18

Распределение электронов по состояниям называют электронной конфигурацией.

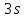Их обозначают символически, например, так:. Это означает, что в атоме имеются два–электрона, два-электрона, шесть-электронов и один-электрон . Это электронная конфигурация атома.

Оболочку (или подоболочку) полностью заполненную электронами называют замкнутой.