
17.3 Спин электрона
Во
внешнем магнитном поле собственные
значения энергии атома водорода
изменяются и для их вычисления используется
формула (17.23). В магнитном поле состояние
с данным главным квантовым числом
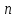 распадается на несколько подсостояний
со значениями энергии несколько большими
(или несколько меньшими) энергии этого
состояния в отсутствие магнитного поля.
Это приводит к расщеплению энергетических
уровней, а следовательно, и спектральных
линий (эффект Зеемана (1896 г.)).
распадается на несколько подсостояний
со значениями энергии несколько большими
(или несколько меньшими) энергии этого
состояния в отсутствие магнитного поля.
Это приводит к расщеплению энергетических
уровней, а следовательно, и спектральных
линий (эффект Зеемана (1896 г.)).
Однако
было обнаружено, что в магнитном поле
расщепляются даже те энергетические
уровни, которые соответствуют состояниям
с
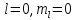 .
Причем эти уровни расщепляются на два
подуровня. Такое расщепление можно
объяснить, предположив, что электрон
обладает собственным магнитным моментом
и формула для энергетических уровней
примет вид
.
Причем эти уровни расщепляются на два
подуровня. Такое расщепление можно
объяснить, предположив, что электрон
обладает собственным магнитным моментом
и формула для энергетических уровней
примет вид
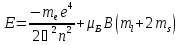 , (17.24)
, (17.24)
При
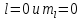 это выражение приводит к двум уровням
энергии, если предположить, что
это выражение приводит к двум уровням
энергии, если предположить, что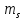 может принимать два значения
может принимать два значения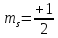 и
и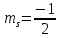 .
.
В
1925 г. Гаудсмит и Уленбек для объяснения
этого факта выдвинули гипотезу о наличии
у электрона собственного момента –
спина. Аналогично орбитальному моменту
определенные значения в одном и том же
состоянии могут иметь квадрат спина
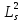 (а значит и модуль спина
(а значит и модуль спина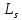 )
и одна из его проекций
)
и одна из его проекций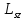 :
:
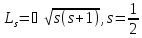 , (17.25)
, (17.25)
где
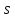 – спиновое квантовое число,
– спиновое квантовое число,
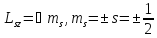 . . (17.26)
. . (17.26)
Значение
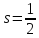 получено из следующих соображений.
Аналогично орбитальному моменту число
возможных значений проекции
получено из следующих соображений.
Аналогично орбитальному моменту число
возможных значений проекции ,
соответствующих данному значению
,
соответствующих данному значению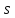 ,
равно
,
равно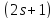 .
Экспериментально было установлено, что
это число для электрона равно двум, т.е.
.
Экспериментально было установлено, что
это число для электрона равно двум, т.е.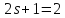 ,
откуда
,
откуда .
Число
.
Число называетсямагнитным
спиновым числом.
называетсямагнитным
спиновым числом.
Отметим,
что спином обладает подавляющее
большинство частиц. Например, у протона
и нейтрона
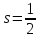 ,
а у фотона
,
а у фотона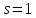 .
.
Опыты
Штерна и Герлаха (1921г.) явились убедительным
доказательством наличия у электрона
спина. Они наблюдали расщепление надвое
пучка атомов, находящихся в
s-состоянии,
при прохождении через неоднородное
магнитное поле. В s-состоянии
орбитальный момент импульса электрона,
а значит, и его орбитальный магнитный
момент, равен нулю (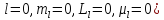 .
Факт раздвоения атомного пучка можно
объяснить только тем, что вs-состоянии
существует собственный магнитный момент
.
Факт раздвоения атомного пучка можно
объяснить только тем, что вs-состоянии
существует собственный магнитный момент
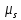 ,
проекция которого
,
проекция которого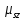 может принимать только два значения.
Результаты измерений показывают, что
может принимать только два значения.
Результаты измерений показывают, что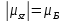 .
.
Итак, спиновый магнитный момент и его проекция на произвольную ось определяются как
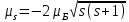 ,
,
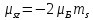 ,
(17.27)
,
(17.27)
причем
при
 магнитное
спиновое число принимает два значения
магнитное
спиновое число принимает два значения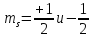 .
Принято говорить, что спиновый
магнитный момент электрона равен одному
магнетону Бора (
.
Принято говорить, что спиновый
магнитный момент электрона равен одному
магнетону Бора (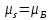 ).
Такая терминология обусловлена тем,
что при измерении магнитного момента
мы обычно измеряем его проекцию, а она
как раз и равна одному
).
Такая терминология обусловлена тем,
что при измерении магнитного момента
мы обычно измеряем его проекцию, а она
как раз и равна одному .
.
Спин – квантовая величина, не имеющая классического аналога. Он ничего общего не имеет с представлением о вращающемся электроне (волчке), как первоначально предполагали (spin – вращение). Спин характеризует внутреннее свойство электрона подобно массе и заряду.
Таким
образом, состояние электрона в атоме
(и состояние самого атома) характеризуется
четырьмя квантовыми числами
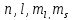 и
волновая функция имеет вид
и
волновая функция имеет вид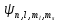 .
.
