Модуль 2.24

Глава 17 Физика атомов

17.1 Атом водорода

Рассмотрим систему, состоящую из неподвижного ядра с зарядом и движущегося вокруг него электрона. При такая система называется водородоподобным ионом, при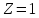она представляет собой атом водорода.

Потенциальная энергия взаимодействия электрона с ядром в такой системе равна

, (17.1)

где – расстояние электрона от ядра.

Уравнение Шредингера в этом случае имеет вид:

(17.2)

Поле (17.1), в котором движется электрон, является центрально-симметричным, т.е. зависит от . Поэтому целесообразно задачу решать в сферической системе координат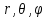. Остановимся лишь на сути процесса решения и на анализе окончательных результатов.

Решение уравнения (17.2) проводят методом разделения переменных с учетом стандартных требований, налагаемых на -функцию: она должна быть однозначной, конечной, непрерывной и гладкой. В процессе решения обнаруживается, что этим требованиям можно удовлетворить в следующих случаях: 1) при любых положительных значениях энергии; 2) при дискретных отрицательных значениях энергии, равных

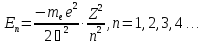(17.3)

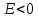Случай соответствует электрону, пролетающему вблизи ядра и удаляющемуся снова на бесконечность. Случайсоответствует электрону, связанному с ядром.

Нас будут интересовать связанные состояния электрона. Для 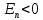собственные функции уравнения (17.2), т.е.-функции, содержат, как выяснилось, три целочисленных параметра:

, (17.4)

где называютглавным квантовым числом, оно совпадает с номером уровня энергии (17.3). Параметрыипредставляют собойорбитальное и магнитное квантовые числа, физический смысл которых будет выяснен в дальнейшем.

Решения, удовлетворяющие стандартным условиям, получаются при значениях , не превышающих . Таким образом, при данномквантовое числоможет приниматьзначений:

. (17.5)

В свою очередь, при данном квантовое числоможет приниматьразличных значений:

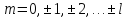. (17.6)

Энергия электрона (17.3) зависит только от главного квантового числа. Отсюда следует, что каждому собственному значению(кроме случая) соответствует несколько собственных функций, отличающихся значениями квантовых чисел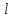и. Это означает, что электрон может иметь одно и то же значение энергии, находясь в нескольких различных состояниях. Например, энергией=2) обладают четыре состояния:.

Кратность вырождения. Состояния с одинаковой энергией называют вырожденными, а число различных состояний с определенным значением энергии –кратностью вырождения данного энергетического уровня.

Кратность вырождения -го уровня водородоподобного атома можно определить, исходя из возможных значенийи. Каждому из-значений квантового числасоответствуетзначений числа. Поэтому полное число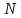различных состояний для данногоравно

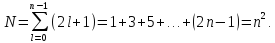(17.7)

Следовательно, кратность вырождения -го энергетического уровня равна.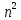

В действительности, как будет показано в дальнейшем, это число надо удвоить из-за наличия собственного момента (спина) у электрона. Таким образом, кратность вырождения -го энергетического уровня

(17.8)

Символы состояний Различные состояния электрона в атоме принято обозначать малыми буквами латинского алфавита в зависимости от значения орбитального квантового числа :

Квантовое число 0 1 2 3 4 5

Символ состояния s p d f g h (17.9)

Принято говорить о s-состоянии (или s-электроне), p-состоянии (или p-электроне) и т.д.

Значение главного квантового числа указывают перед символом состояния с данным. Например, электрон, имеющий главное квантовое числои, обозначают символом. Выпишем последовательно несколько состояний электрона:

1s; 2s; 2p; 3s; 3p; 3d …

Схема уровней энергии для атома водорода в различных состояниях показана на рис. 1.

Мы знаем, что испускание и поглощение света происходит при переходах электрона с одного уровня на другой. В квантовой механике доказывается, что для орбитального квантового числа имеется правило отбора

. (17.10)

Правило отбора является следствием закона сохранения момента импульса при испускании кванта. Фотон обладает собственным моментом импульса – спином, равным единице (в единицах ). При испускании фотон уносит из атома этот момент, а при поглощении привносит, вследствие чего орбитальное квантовое числоменяется на единицу.

Рис. 1

На рис. 1 показаны переходы, разрешенные правилом отбора (17.10). Переходы, приводящие к возникновению серии Лаймана, можно записать в виде:

,

серии Бальмера соответствуют переходы

и

и т.д.

Состояние 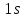является основным состоянием атома водорода. В этом состоянии атом обладает минимальной энергией.