16.6 Операторы в квантовой механике

В квантовой механике большую роль играет понятие оператора. Под оператором подразумевают правило, посредством которого одной функции сопоставляется другая функциятех же самых переменных. Символически это записывается следующим образом:

(16.30)

Здесь – символическое обозначение оператора (буквасо «шляпкой»). Под символом оператора скрывается совокупность действий, с помощью которых исходная функцияпревращается в другую функцию. Примером оператора может служить умножение на некоторую функцию. Тогдаи, следовательно,. Оператором является также дифференцирование по, т.е.и т.д., оператор Лапласа.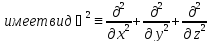

Если рассматривать функцию в уравнении Шредингера (16.8) как оператор, то это уравнение можно записать в виде:

, (16.31)

где

-оператор полной энергии частицы – гамильтониан.

В квантовой механике каждой физической величине сопоставляется оператор(для каждой величины оператор обозначается по-своему: для энергии -, для импульса -, для момента импульса -и т.д.). Решая уравнение

, (16.32)

находим собственные значения оператора. Функции, являющиеся решением этого уравнения и удовлетворяющие стандартным условиям, называют собственными функциями оператора.

Как уже говорилось, физический смысл могут иметь лишь такие решения, которые всюду конечные, однозначные, непрерывные и гладкие. Эти условия называют естественными или стандартными.

Общее утверждение квантовой механики заключается в том, что среднее значение любой физической величины находится по формуле

, (16.33)

где – оператор физической величины.

Мы уже знаем, что среднее значение координаты частицы, если известна ее-функция, определяется как

, (16.34) где интегрирование проводится по интересующей нас области, а функция является нормированной, т.е. удовлетворяет условию:

.

Значительно сложнее задача о нахождении среднего значения проекции импульса частицы, состояние которой задается определенной пси-функцией.

Весьма громоздкий расчет приводит к следующему результату:

. (16.35)

Сопоставив (16.33) с (16.34) и (16.35), приходим к выводу, что операторами величин иявляются

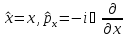. (16.36)

Аналогично для операторов .

Операторы иявляются основными в квантовой физике.

Общее правило, позволяющее находить операторы других физических величин, таково: формулы классической физики для связи между величинами в квантовой теории следует рассматривать как формулы, связывающие операторы этих величин.

Так, например, квадрат импульса в классической механике равен

.

Поэтому оператор квадрата импульса

В результате получим

, (16.37)

где оператор –оператор Лапласа.

Аналогично находим оператор кинетической энергии:

. (16.38)

Отсюда получается оператор полной энергии – гамильтониан:

. (16.39)

Зная выражения операторов , можно найти средние значения,,по формуле (16.33), если известна ψ-функция частицы.

Найдем, наконец, оператор момента импульса. Согласно классической механике

.

В соответствии с общим правилом оператор проекции момента импульса, например, на ось 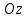имеет вид:

. (16.40)

В дальнейшем нам придется использовать этот оператор, но не в декартовой, а в сферической системе координат . В этой системе оператор, имеет вид

. (16.41)

Это показано в задаче 4.

Задачи

Задача 1

Получить решение уравнения Шредингера для случая свободной частицы массы , движущейся вдоль осив положительном направлении.

Решение

Для свободной частицы (), движущейся вдоль оси, уравнение Шредингера для стационарных состояний (16.8) будет иметь вид:

,

или

(1)

Так как потенциальная энергия частицы 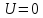, то полная энергияравна.

Введем обозначение: . Тогда

,

где – импульс частицы. Учитывая выражение для, можно записать:

Общее решение этого уравнения имеет вид:

,

где первый член соответствует движению в положительном, а второй – в отрицательном направлении оси . Так как по условию задачи частица движется в положительном направлении оси, то в решении нужно оставить только первый член, т.е. положить

.

Отметим, что решение возможно при любых значениях , а значит, и, т.е. энергетический спектр свободной частицы – сплошной.

В соответствии с (16.10) для полной волновой функции будем иметь

.

Это и есть уравнение плоской волны, распространяющейся вдоль положительного направления оси . Действительно, нам известно, такая волна определяется уравнением вида:

.

В нашем случае , а волновое числоопределяется соотношением, откуда, что совпадает с соотношением для длины волны де-Бройля рассматриваемой частицы.

Таким образом, искомое решение уравнения Шредингера для сводобной частицы представляет собой плоскую волну де-Бройля.

Задача 2

Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме шириной с абсолютно непроницаемыми стенками (). Найти вероятность нахождения частицы в интервале ().

Решение

Согласно (16.20) -функция в основном состоянии () имеет вид

Искомая вероятность

,

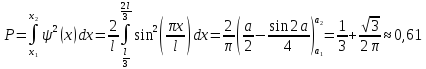где введена новая переменная .

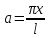Задача 3

Частица массы находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Координатыинаходятся в интервале соответственно (0,) и (0,), гдеи– стороны ямы. Найти возможные значения энергии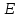и нормированныеψ -функции частицы.

Решение

В этом случае уравнение Шредингера (16.8) имеет вид:

, (1)

(в пределах ямы ).

Учитывая, что ина двух сторонах ямы (и),-функцию внутри ямы удобно искать в виде произведения синусов

(2)

Возможные значения инайдем из условия обращения ψ-функции в нуль на противоположных сторонах ямы:

;

; (3)

После подстановки (2) в уравнение (1) получим , и, учитывая выражение дляв (1), получим

. (4)

Постоянную в (2) находим из условия нормировки

,

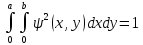откуда следует, что .

Следовательно, нормированная ψ-функция будет иметь вид

.

Задача 4

Показать, что в сферической системе координат оператор .

Решение

Рис. 1

Запишем связь между декартовыми и сферическими координатами с помощьюрис. 1.

,

, (1)

.

C помощью этих формул выразим частную производную по через производные

по .

(2)

Вычислив частные производные ,,формул (1), подставим результаты в (2) и получим

. (3)

Из сопоставления с (1) видим, что (3) можно переписать так:

Учитывая выражение для (16.40) получим, что

.

Тесты

1. С помощью волновой функции Ψ можно определить

(1) траекторию движения частицы, (2) вероятность обнаружения частицы в разных точках пространства, (3) длину волны де Бройля в разных точках пространства, (4) импульс частицы в разных точках пространства.

2. При одномерном движении вдоль оси X вероятность обнаружения частицы в интервале [x, x+dx] равна

(1) , (2) , (3), (4) .

3. Траектория движения микрообъекта

(1) определяется его волновой функцией, (2) не существует, (3) находится из соотно-шения неопределенностей Гейзенберга, (4) находится решением уравнения Шредингера.

4. Волновая функция Ψ является

(1) вероятностью обнаружения частицы в разных точках пространства, (2) плотностью вероятности обнаружения частицы в разных точках пространства, (3) амплитудой волны де Бройля, (4) амплитудой вероятности обнаружения частицы в разных точках пространства.

5. Cтационарное уравнение Шредингера для частицы массы m записывается следующим образом

(1) 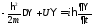, (2),

(3) , (4) .

6. Решая стационарное уравнению Шредингера можно определить,

(1) волновую функцию частицы и ее положение в пространстве, (2) волновую функцию, кинетическую и потенциальную энергии частицы, (3) только энергетические уровни, (4) волновую функцию частицы и ее энергетические уровни.

7. Нестационарное уравнение Шредингера для частицы массы m записывается следующим образом

(1) , (2) ,

(3) ,(4) .

8. Туннельный эффект-это явление, при котором квантовая частица проходит через потенциальный барьер при

(1) E=U₀, (2) E>U₀, (3) E<U₀, (4) E>0,

где E - кинетическая энергия частицы, U₀ - высота потенциального барьера.

9. Коэффициентом прозрачности D потенциального барьера называется

(1) отношение импульса прошедших частиц к импульсу падающих,

(2) отношение импульса падающих частиц к импульсу прошедших.

(3) отношение плотности вероятности потока прошедших частиц

к плотности вероятности потока падающих,

4) отношение плотности вероятности потока падающих частиц

к плотности вероятности потока прошедших.

10. Электрон наталкивается на потенциальный барьер конечной высоты U₀. При каком значении кинетической энергии Е электрона он не пройдет через потенциальный барьер:

(1) среди указанных ответов нет правильного, (2) E=U₀, (3) E>U₀, (4) E<U₀.

11. Коэффициент прозрачности D потенциального барьера зависит от ширины l барьера по закону

(1) D не зависит от l. (2) D ~ e^-kl, (3) D ~ l, (4) D ~ l².

12. С увеличением ширины l потенциального барьера коэффициент прозрачности D барьера

(1) уменьшается, (2) увеличивается, (3) при больших l - увеличивается, при малых l – уменьшается, (4) при малых l - увеличивается, при больших l – уменьшается.

13. К специфическим квантовым явлениям относится

1. туннельный эффект, (2) эффект Холла, (3) релятивистское увеличение массы, (4) интерференция волн.

14. С увеличением высоты U₀ потенциального барьера коэффициент прозрачности D барьера

(1) D не зависит от U₀, (2) при больших U₀ - увеличивается, при малых U₀ – уменьшается, (3) уменьшается, (4) увеличивается.

15. С увеличением массы m квантовой частицы коэффициент прозрачности D барьера

(1) увеличивается, (2) уменьшается, (3) D ~1/m, (4) D не зависит от m.

16. Вероятность обнаружить частицу на участке [a,b] одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле , гдеw(x) – плотность вероятности, определяемая волновой функцией Ψ(x). Если Ψ(x) имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке равна

(1) 50%, (2) ≈33%, (3) ≈67%, (4) 75%, (5) ≈83%.

17. Стационарным уравнением Шредингера для линейного гармонического осциллятора является уравнение

(1) , (2),

(3) , (4) .

18. Вероятность обнаружить частицу на участке [a,b] одномерного потенциального ящика с бесконечно высокими стенками вычисляется по формуле , гдеw(x) – плотность вероятности, определяемая волновой функцией Ψ(x). Если Ψ(x) имеет вид, указанный на рисунке, то вероятность обнаружить электрон на участке равна

(1) ≈33%, (2) 59%, (3) ≈17%, (4) ≈67%, (5) ≈83%.

19. Стационарным уравнением Шредингера для электрона в атоме водорода является уравнение

(1) , (2),

(3) , (4).

20. Стационарным уравнением Шредингера для электрона в водородоподобном ионе является уравнение

(1) , (2),

(3) , (4).

21. Стационарным уравнением Шредингера для свободной частицы является уравнение

(1) , (2) ,

(3) , (4).

22. Стационарным уравнением Шредингера для свободной частицы, движущейся вдоль оси X, является уравнение

(1) , (2),

(3) , (4).

23. Стационарным уравнением Шредингера для частицы, движущейся в одномерном потенциальном ящике с бесконечно-высокими стенками, является уравнение

(1) , (2), (3), (4).

24. Стационарным уравнением Шредингера для частицы, движущейся в трехмерном потенциальном ящике с бесконечно-высокими стенками, является уравнение

(1) , (2), (3), (4).

26