
16.5 Потенциальные барьеры
Сначала
рассмотрим простейший случай –
прямоугольный потенциальный барьер,
когда потенциальная энергия
 зависит только от одной координаты
зависит только от одной координаты ,
причем при
,
причем при претерпевает скачок (рис. 5).
претерпевает скачок (рис. 5).

Рис. 5
У такого барьера
 (16.26)
(16.26)
Пусть
слева на границу барьера высотой
 налетает с полной энергией
налетает с полной энергией частица.
частица.
Если
 ,
то классическая частица беспрепятственно
проходит над барьером. Если
,
то классическая частица беспрепятственно
проходит над барьером. Если ,
то классическая частица отражается от
барьера и движется в обратном направлении.
,
то классическая частица отражается от
барьера и движется в обратном направлении.
Если
квантовая частица обладает энергией
 ,
то имеется отличная от нуля вероятность
того, что она отразится от барьера. При
,
то имеется отличная от нуля вероятность
того, что она отразится от барьера. При квантовая частица может проникнуть
через потенциальный барьер в классически
запрещенную область.
квантовая частица может проникнуть
через потенциальный барьер в классически
запрещенную область.
Оценим вероятность проникновения частицы под барьер.
При
 уравнение Шредингера (16.8) имеет вид:
уравнение Шредингера (16.8) имеет вид:

или

Обозначив
 ,
получим уравнение вида:
,
получим уравнение вида:

Решениями
этого уравнения являются две экспоненты:
 .
Экспонента
.
Экспонента физического смысла не имеет и должна
быть отброшена, так как при
физического смысла не имеет и должна
быть отброшена, так как при

 ,
а волновая функция должна быть конечной.
,
а волновая функция должна быть конечной.
Следовательно,
при
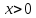 частица с энергией
частица с энергией имеет волновую функцию
имеет волновую функцию , и плотность вероятности обнаружения
частицы под барьером равна
, и плотность вероятности обнаружения
частицы под барьером равна
 , (16.27)
, (16.27)
где
 .
.
Видно,
что с увеличением глубины проникновения
 плотность вероятности
плотность вероятности убывает экспоненциально. Это убывание
происходит тем быстрее, чем больше
разность
убывает экспоненциально. Это убывание
происходит тем быстрее, чем больше
разность .
Обычно глубину проникновения определяют
как расстояние
.
Обычно глубину проникновения определяют
как расстояние ,
на котором
,
на котором убывает в
убывает в раз. При этом
раз. При этом и
и
 . (16.28)
. (16.28)
Можно
убедиться, что для электрона
 кг) при
кг) при
 глубина
проникновения
глубина
проникновения
 Å.
Å.
Так, на расстояние такого порядка удаляются от поверхности металла электроны проводимости, энергия которых примерно на 10-3 эВ меньше глубины потенциальной ямы, удерживающей электроны внутри металла. Яма создается взаимодействием электрона с положительными ионами, расположенными в узлах кристаллической решетки металла.
Туннельный
эффект.
Способность квантовых частиц
«просачиваться» через потенциальный
барьер, абсолютно непрозрачный с
классической точки зрения, приводит к
туннельному эффекту. Он заключается в
следующем. Если частица с энергией
 налетает на некоторый потенциальный
барьер
налетает на некоторый потенциальный
барьер ,
то она с определенной вероятностью
может пройти сквозь барьер как бы по
туннелю, то есть пройти область, где
,
то она с определенной вероятностью
может пройти сквозь барьер как бы по
туннелю, то есть пройти область, где .
.

Рис. 6
Соответствующий расчет показывает, что в случае потенциального барьера произвольной формы (рис. 6) вероятность прохождения частицы сквозь барьер, то есть коэффициент прозрачности барьера равен
 , (16.29)
, (16.29)
Это
приближенное равенство, оно тем точнее,
чем меньше
 по сравнению с
по сравнению с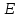 .
.
Туннельный эффект – квантовое явление, не имеющее аналога в классической физике (где такого в принципе быть не может).
В
классической физике проникновение
частиц под барьер запрещено, поскольку
в этой области кинетическая энергия
оказывается отрицательной, чего быть
не может. В квантовой механике нет
деления полной энергии
 на кинетическую и потенциальную, так
как соотношение неопределенностей не
позволяет одновременно их точно задать.
на кинетическую и потенциальную, так
как соотношение неопределенностей не
позволяет одновременно их точно задать.
Туннельный эффект объясняет многие физические явления, например, холодную эмиссию электронов из металлов, альфа-распад радиоактивных ядер, спонтанное деление ядер, ядерные реакции, когда по классическим представлениям кинетической энергии сталкивающихся ядер недостаточно для преодоления кулоновского потенциального барьера между ними.
